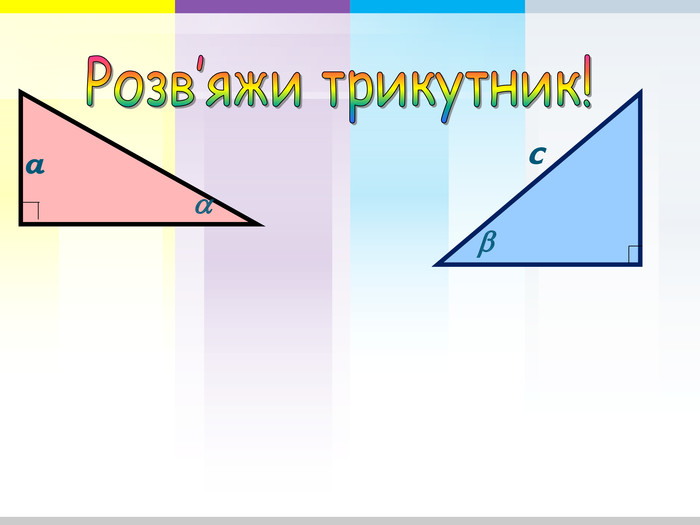
Урок "Узагальнення та систематизація знань з теми «Теорема Піфагора» "

Тема: Узагальнення та систематизація знань з теми  «Теорема Піфагора»
Мета: Систематизувати й узагальнити теоретичні зання, вміння та навички учнів з теми;
формувати вміння застосовувати набуті знання до розв’язування задач;
активізувати пізнавальну діяльність учнів;
розвивати логічне та креативне мислення;
прищеплювати інтерес до математики;
виховувати активність, увагу, кмітливість.

Обладнання: інтерактивна дошка, диск з відповідними файлами, картки із задачами та фішки із відповідями для математичного лото, задачі записані на «папірусі», таблиці для підрахунку загальної кількості балів, медалі Піфагора.
Тип уроку: урок-вікторина

                                  Хід уроку.

І. Вступ.
Епіграф уроку

 Нехай зруйнується століть перепона,
Нехай на мить затремтять віки.
Ми знаємо його – Піфагор навколо
Він бога творіння, він символ науки.

Перед уроком необхідно розбити клас на дві команди, які обирають капітанів і дають назву команді. Для швидкого підбиття підсумків конкурсів ,для оцінювання роботи кожного учня підготувати таблицю для загальної кількості балів, що набрала команда та індивідуально кожен учень.

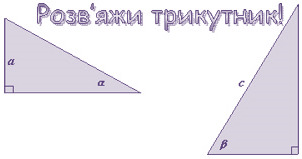
ІІ. Розминка.
Кожна команда по черзі усно намічує хід розв’язання задачі, умови яких подано на інтерактивній дошці

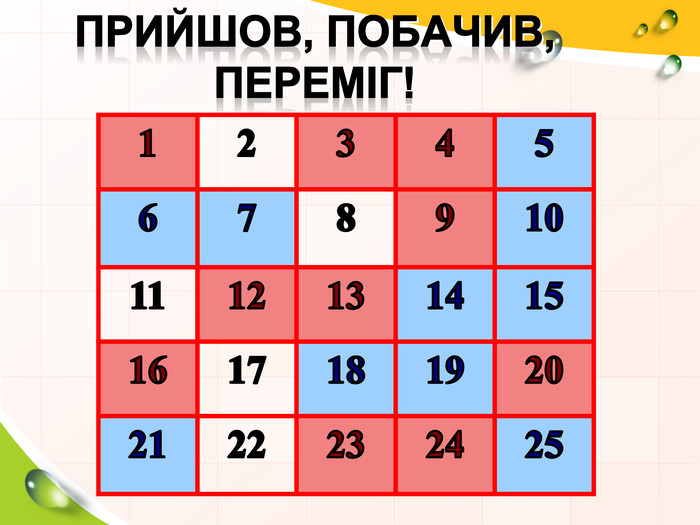
ІІІ. Конкурс «Прийшов, побачив, переміг».
На протязі 10 - 15 секунд учням демонструється таблиця з числами від 1 до 25. 10 квадратиків зафарбовані у червоний колір – колір першої команди, а 10 – у зелений – колір другої команди. Далі таблиця закривається. Учні називають номер квадратика. Якщо він має колір команди, то до результату команди додається 2 бали, якщо колір суперника, то при правильній відповіді команда отримує лише 1 бал. А якщо – колір білий, то запитання простіші і команда отримує лише 0,5 бала.

Запитання.
Для першої команди:
1. Сформулювати означення прямокутного трикутника.
2. Косинусом гострого кута прямокутного трикутника називається …
3. Тангенсом гострого кута прямокутного трикутника називається …
4. Сформулюйте теорему Піфагора.
5. Сформулюйте властивість проекцій та похилих, поведених з однієї точки до даної прямої.
6. Як змінюється синус і тангенс при зростання гострого кута?

 7. cos60⁰= …
8. tg 45⁰= …
9. Чи можуть сторони трикутника бути рівними 3 см, 2 см та 5 см?
10. sin²α+cos²α = …
Для другої команди:
1. Сформулюйте означення рівнобедреного трикутника.
2. Синусом гострого кута прямокутного трикутника називається …
3. Відношення прилеглого катета до протилежного називається …
4. Сформулюй теорему, обернену до теореми Піфагора.
5. Як змінюється косинус та котангенс при зростання кута?
6. Сформулюйте нерівність трикутника.
7. sin 60⁰= …
8. ctg 45⁰= …
9. Яка із сторін прямокутного трикутника є гіпотенузою 10 см, 6, см 8 см?
10. 1+tg²α= …
Загальні питання:
1. Чому дорівнює сума двох гострих кутів прямокутного трикутника?
2. Яка сторона є довшою у прямокутному трикутнику?
3. Як називаються сторони прямокутного трикутника, що утворюють прямий кут?
4. Чиє ім’я носить теорема про катети і гіпотенуз прямокутного трикутника?
5. Чи справедлива рівність sinα = cos (90⁰–α)?

ІV. Гра «Математичне лото»

Учні обєднуються у пять команд по кольорам карток.
Командам пропонуються тексти задач, записаних на картці. Декілька хвилин учні колективно, або індивідуально розв’язують ці задачі. Потім учитель зачитує фішки з відповідями. Якщо відповідь підходить, то команда забирає фішку і накладає її на задачу. Перемагає та команда, яка швидше і правильно закриє усі задачі.

Відмічені кольором задачі учні повинні розвязати біля дошки, відправивши найсильнішого учасника.

Картка для першої команди

Картка для другої команди

Картка для третьої команди

Картка для четвертої команди

Картка для пятої команди

Відповіді

V. Задачі з рукописів китайського математика.

Геометрія – це мистецтво добре вимірювати.

П. Раме

Учням пропонується розв’язати задачу з минулого, записані на згортках паперу, що імітують сувої папірусу. (Кожному учневі окремий папірус. Відповідно маємо 3 групи.)
Учні самостійно розвязують завдання і через 3хв презентують (за бажанням) своє розв’язання біля дошки, отримуючи Медаль Піфагора

Задача 1. «Стрибок мавпи»
На дереві сиділи дві мавпочки: Одна – на самій верхівці дерева, інша – на висоті 10 ліктів від землі. Другій мавпочці захотілося напитися води з джерела, що знаходиться на відстані 40 ліктів від дерева. Вона злізла з дерева і пострибала до води. У той самий час перша зістрибнула з дерева і потрапила до того ж джерела. Обидві мавпочки подолали однакову відстань. Скажи, о мудра людина, з якої висоти стрибнула друга мавпочка.

Задача 2. «Зламаний бамбук».
Бамбук, що має 40 ліктів у висоту, було зламано вітром. Його верхівка торкнулася землі за 20 ліктів від основи стовбура. Скажи, о юний математик, на якій відстані від землі було зламано бамбук?

Задача 3. «Дві вежі»
Дві вежі висотою 30 і 40 футів, розміщено одна від одної на відстані 50 футів. Між ними знаходиться фонтан, до якого одночасно з маківок веж з однаковою швидкістю вилетіли два голуби. О, майбутній Піфагоре, скажи, яка відстань від фонтана до кожної з двох веж, якщо голуби долетіли одночасн

VІ. Лірична пауза.

Чи знаєте Ви, що…

…У Франції та Німеччині в епоху середньовіччя теорему Піфагора називали «ослячим мостом»?

Учнів, що запам’ятовували теорему без розуміння, називали віслюками, оскільки вони не могли перейти через міст – теорему Піфагора.

…У математиків арабського Сходу ця теорема отримала назву «теореми нареченої»?

Справа в тому, що в деяких списках «Начал» Евкліда ця теорема називалась «теоремою німфи» за схожість креслення з бджілкою, метеликом, що грецькою називалося «німфа». Але цим словом греки називали богинь, а також молодих жінок і наречених. Перекладаючи з грецької, арабський перекладач, не звернувши уваги на креслення, переклав слово «німфа» як «наречена», а не «метелик». Так з’явилася лагідна назва відомої теореми – «теорема нареченої».

Учням для зняття навантаження пропонується прослухати казку про теорему Піфагора у виконанні однієї учениці

 В одному із грецьких міст жили двоє нерозлучних друзів, і кожен з них мав ім’я Катет. Дружили вони ще із раннього дитинства і поклялися, що ніхто в житті, хоч би як воно не складалося, не заважатиме їхній дружбі. Були вони обидва скромні, чесні хлопці, навіть мали однакові уподобання. Одного разу зустріли дівчину на ім’я Гіпотенуза і полюбили її. Дівчина була дуже гарна: висока, струнка, з довгим чорним волоссям та виразним милим обличчям. Не знала вона кому із хлопців віддати перевагу, бо подобались вони їй обидва. Кожен із хлопців мріяв про Гіпотенузу, та не хотів ставати на перешкоді своєму другові. І ось, не залежно один від одного, пішли друзі із міста, що б не заважати. Один думав так: «Піду я звідси, адже Катет мій друг, і я хочу, щоб він був щасливий. Не заважатиму його щастю – нехай він зостається з Гіпотенузою». Такі ж думки були і в іншого Катета.
Один із хлопців пішов на північ, а другий на схід.
Хоч розійшлися вони і далеко були один від одного. Та зв’язує їх думка про Гіпотенузу.
Тому теорема «Катет²+Катет²=Гіпотенуза²», – ніби схрещені шпаги у бою між двома Катетами через Гіпотенузу.

V ІІ. Зупинка “Тести на теорему Піфагора”.

“Розв’язування трикутників” пов'язане з розв’язанням прямокутних трикутників, що вивчаються в 8 класі, які зазвичай розв’язуються теоремою Піфагора. 9 тестів, з них 6 тестів відкриті, тобто потрібно, розв’язати, вибрати відповіді з чотирьох відповідей і 3 тести закриті, тобто не мають відповіді. Відповідь потрібно самим знайти. Бажаю успіху! (дається 5 хвилин)

Для перевірки правильності виконання завдань, відповіді проектуються на екран.

Тести

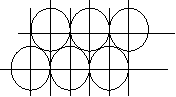
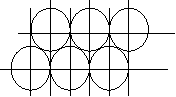
1. Вкажіть, який з малюнків містить трикутники, до яких застосовна теорема Піфагора

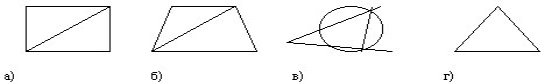
2. Сторона квадрата рівна 3 см, тоді їх діагональ рівна:

а) 9 см; б) 6 см; в) 3 см; г) 32 см.

3. У рівнобедреному трикутнику бічна сторона рівна 10 см, а основа– 16 см, тоді висота опущена на основу, рівна:

а) 241 см; б) 6см; в) 26 см; г) 6 см.

4. З однієї точки на пряму опущені перпендикуляр і похила. Якщо перпендикуляр рівний 9 см, а похила – 15 см, то довжина проекції :

а) 12 см; б) 334 см; в) 26 см; г) 6 см.

5. З точки D до кола з центром в точці О проведена дотична DF. Якщо OD =17 см, а FD =15 см, то радіус кола рівний:

а) 2 см; б) 8 см; в) 32 см; г) 42 см.

6. Даний прямокутний трикутник ABC. Гіпотенуза AС=10 см, sinc=0,3. Знайдіть катет AB. Відповідь: AB=3 см

7. У рівнобедреному трикутнику одна сторона рівна 11 см, а друга – 4 см. Знайдіть третю сторону. Відповідь: : 11 см.

8. В прямокутному трикутнику. ABC:AC=17 см, BC=8 см, AB=15 см.  Знайдіть cosC. Відповідь: cosC=8/17.

9. У колі з центром в точці О проведена хорда АВ, рівна 18 см, якщо відстань від центру кола до хорди рівна 12 см, то радіус кола рівний:

а) 15 см; б) 6 см; в) 613 см; г) 37 см.

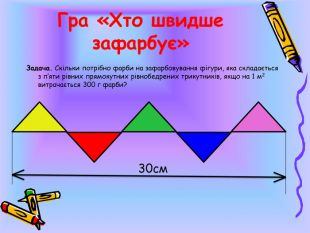
VІІІ. Гра «Хто швидше зафарбує»
Розв’язати індивідуально прикладну задачу, спроектовану на дошку. Хто швидше це зробить, принесе команді 5 балів.
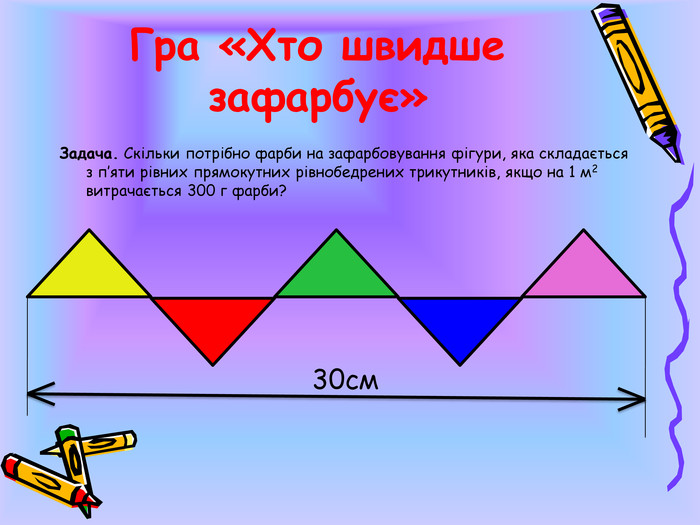
Задача. Скільки потрібно фарби на зафарбовування фігури, яка складається з п’яти рівних прямокутних рівнобедрених трикутників, якщо на 1 м² витрачається 300 г фарби? (27кг)

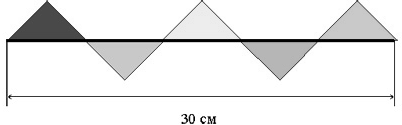
ІХ. Підбиття підсумків уроку-вікторини.
              1.  Кожний   з    вас    оберіть   для    себе задачу «по силам», розв’яжіть її і підіб’ємо  підсумок всієї нашої праці.

           І варіант           ІІ варіант

1. 1 бал

                                                                                           X                  3

          2                         x                   

                     22                                                                               33

2.           1 бал

                                                                                                     60

     a              х                                                                   x              2

3.           2 бали

         2                                                                                                         

                                                                                           x

                                                                                                         3

                    x                                                                                                 

4.          5 балів

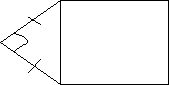
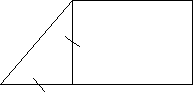                      B                      C                                          A                     M

                                                                                           C 

  A              B₁                        D                                           B                     D

ВСDВ₁     - квадрат      АМDВ – квадрат

ВСDВ = 4 см²       АМDВ =100 см²

________________      _________________

АВ²- ?        АС² - ?

2. Рефлексія.
- Що на уроці було найважливішим?
- Що було найцікавішим?
- Що було найскладнішим?
- Над чим слід попрацювати вдома?

3. Хотілося закінчити урок, згадавши вчення Піфагора, адже воно так нам необхідне в житті.

• Твори велике, не обіцяючи великого
• Нічому не дивуйся
• Тимчасова невдача краща від тимчасової удачі
• Не заплющуй очі, коли хочеш спати, не проаналізувавши своїх учинків за минулий день
• Живи з людьми так, щоб твої друзі не стали недругами, а недруги стали друзями
• Не роби нічого ганебного ні в присутності інших, ні таємно. Першим твоїм законом повинна бути повага до самого себе
• Лише неблагородна людина здатна в очі хвалити, а поза очі злословити
• Усе в світі підкоряється числам

Х. Завдання додому.
Повторити теоретичний матеріал, переглянути розв’язування задач. Підготуватися до самостійної роботи.
Розв’язати завдання :

Группа А : ст 134 (рівень А  №1, №4), ст 213 №1010

Группа В: ст 134 (рівень Б  №1, №3), ст 214 №1014

Группа С: ст 134 (рівень Б  №2, №4), ст 221  №1062

Картка для першої команди

Картка для другої команди

Картка для третьої команди

------------Картка для четвертої команди

Картка для пятої команди