Урок "Вектори у просторі"
Формування поняття вектора в просторі та пов'язані з ним поняття абсолютної величини, напрямку, рівності векторів; розгляд дій над векторами.
ПЛАН УРОКУ
Дата «____»_________________ 2020 р.
Предмет: Геометрія
Тема: Декартові координати і вектори у просторі
Тема уроку: Вектори у просторі
Мета уроку:
-Сформувати поняття вектора в просторі та пов’язані з ним поняття абсолютної величини, напрямку, рівності векторів; розглянути дії над векторами;
- Розвивати індивідуальні здібності та пізнавальну активність учнів, просторову уяву, логічне мислення, вміння висловлювати свою думку;
- Виховувати творчу, працелюбну особистість шляхом навчання за допомогою швидкозмінних форм подачі інформації.
Тип уроку: урок вивчення нового матеріалу
Вид уроку: лекція з елементами пошукового практикуму та тестами у форматі ЗНО
Методи: словесні (діалог, монолог), наочні, частково пошукові, евристичні, практичні
Дидактичне забезпечення: робочий зошит з теми «Вектори у просторі», презентація викладача
Обладнання: ноутбук, проектор, екран
«Теорія без практики мертва і безплідна,
практика без теорії неможлива. …»
Рене Декарт
(французький філософ, математик,
фізіолог, фізик)
Хід уроку
- Організаційний момент.
Повідомлення теми і мети уроку.
II. Мотивація навчальної діяльності.
Поміркуйте над змістом приказки: «Сила без голови шаленіє, а розум без сили мліє». Якщо є сила, та треба знати, куди її спрямовувати. Від цього залежить, чи буде пружина стискатися або розтягуватися, чи полетить м‘яч у ворота противника чи у власні та багато іншого. А напрямок сили вкаже вектор.
Уперше поняття вектору як напрямленого відрізка знайшло застосування в механіці для зображення фізичних векторних величин: швидкості, прискорення, сили тощо. Не дивлячись на це, вектор - математичне поняття, оскільки усі операції над векторами виконуються за законами математики. За допомогою векторного методу розв’язується багато різноманітних задач, які не мають іншого способу розв’язання.
Саме тому вивчення поняття вектору є дуже важливим в сучасних умовах розвитку математичних наук.
IІІ. Сприйняття й усвідомлення нового матеріалу.
Допоміжним засобом є презентація викладача, створена у програмі Power Point (ілюстративний матеріал до уроку, перевірка виконаних завдань).
Учні працюють в робочих зошитах.
Пояснення і осмислення навчального матеріалу відбувається за допомогою інтерактивних методів: проводяться пошуковий практикум, гра: «Вірю – не вірю», розв’язуються задачі-тести у форматі ЗНО.
Лекція викладача з елементами бесіди та тестових питань у форматі ЗНО.
Теоретичні відомості
Вектор – це напрямлений відрізок. Його напрям від початку до кінця позначають стрілкою. Позначають
або 
. Довжиною або модулем вектора 
нази
вається довжина відрізка АВ. Будь яку точку простору можна розглядати як вектор. Такий вектор називається нульовим. Позначають нульовий вектор 
або 
.
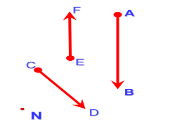
Пошуковий практикум
Назвіть вектори, зображені на рисунку. Укажіть початок і кінець векторів.
Теоретичні відомості
Колінеарні вектори
Два ненульових вектори називаються колінеарними, якщо вони лежать на одній прямій або на паралельних прямих
«ЗНО не за горами» (завдання у форматі ЗНО)
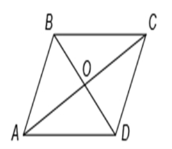
На рисунку зображено паралелограм ABCD, діагоналі якого перетинаються в точці О. Укажіть пару колінеарних векторів.
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
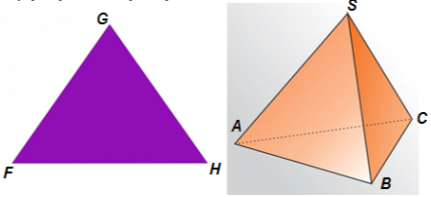
Пошуковий практикум
Вкажіть пари колінеарних
векторів, які є різними:
1) сторонами трикутника FGH;
2) ребрами тетраедра SABC
Теоретичні відомості
Колінеарні вектори
співнапрямлені протилежно напрямлені
Позначається: 
(співнапрямлені), ( протилежно напрямлені)
Які вектори на рисунку спінапрямлені?
Які вектори на рисунку протилежно напрямлені?
Знайти довжини векторів 
; 
; 
.
«ЗНО не за горами» (завдання у форматі ЗНО)
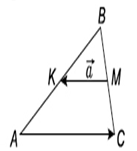На рисунку зображено трикутник АВС, точки К іМ – середини сторін АВ і ВС
відповідно. Укажіть правильну рівність, якщо
=
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
Теоретичні відомості
Рівність векторів
Вектори називаються рівними, якщо вони
співнапрямлені та їх довжини рівні.
Пошуковий практикум
Чи можуть бути рівними вектори на рисунку?
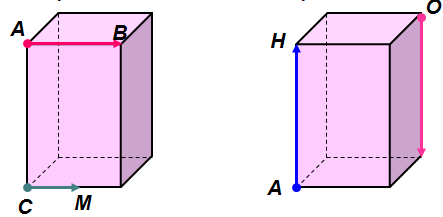
рис. 1 рис. 2
Теоретичні відомості
Дії над векторами
- Додавання
- Віднімання
- Множення вектора на число
Додавання векторів
- Правило трикутника
- Правило паралелограма
- Правило многокутника
- Правило паралелепіпеда
Правило трикутника
Для додавання двох векторів необхідно:
-
Відкласти від будь-якої точки А вектор ,
рівний вектору
-
Від точки В відкласти вектор , рівний
-
Вектор
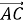називається сумою векторів і .
Якщо вектори колінеарні, то їх сума
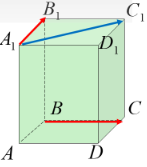
ABCDA1B1C1D1 - паралелепіпед.
Укажіть вектор, початком і кінцем якого є вершини паралелепіпеда, що дорівнює:
+
Відповідь: 
ЗНО не за горами (завдання у форматі ЗНО)
На рисунку зображено вектори і . Який із наведених векторів дорівнює вектору 
?
Теоретичні відомості
Правило паралелограма
Для додавання двох векторів необхідно:
-
Від будь-якої точки А відкласти вектор , рівний вектору
-
Від точки А відкласти вектор
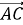, рівний
- Добудувати фігуру до паралелограма, провівши додаткові лінії, паралельні до даних векторів
-
Діагональ паралелограма – сума векторів
«ЗНО не за горами»(завдання у форматі ЗНО)
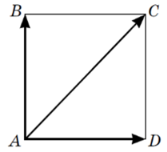
На рисунку зображено квадрат ABCD. Укажіть правильну векторну рівність.
Правило многокутника
Сума векторів дорівнює вектору, який проведений з початку першого в кінець останнього (при послідовному відкладанні)
Приклад
Знайти суму векторів 
+ 
+ 
+ 
+ 
Відповідь:
Пошуковий практикум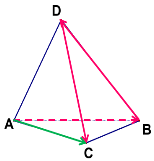
Відповідь:
Теоретичні відомості
Правило паралелепіпеда
Дано вектори , і 
,що не лежать в одній площині. Побудуємо паралелепіпед так, щоб відрізки, що зображають задані вектори, були його ребрами. Тоді вектор-сума є діагоналлю паралелепіпеда, побудованого на векторах-доданках.
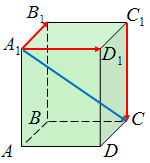Пошуковий практикум
ABCDA1B1C1D1 паралелепіпед.
Укажіть вектор початком і кінцем якого є вершини паралелепіпеда, що дорівнює:
+ 
+ 
(за правилом паралелепіпеда)
Відповідь: 
Теоретичні відомості
Вектори протилежні, якщо вони протилежно напрямлені та їх довжини рівні.
Віднімання векторів
Різницею векторів
і називається такий вектор
, сума якого з вектором дорівнює вектору
.
- = ⇔ + = або - = + (- )
Пошуковий практикум
ABCDA1B1C1D1 паралелепіпед .
Укажіть вектор, початком і кінцем якого є вершини паралелепіпеда, що дорівнює: -
Відповідь:
Теоретичні відомості
Множення вектора на число
Добутком ненульового вектора
на число k називається такий вектор , довжина якого дорівнює | k | ∙ ||, причому вектори і співнапрямлені, коли ≥ 0, і протилежно напрямлені, коли < 0.
«ЗНО не за горами» (завдання у форматі ЗНО)
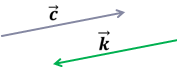
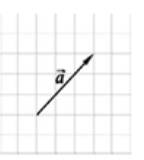
На рисунку зображено вектор . Який з наведених векторів дорівнює вектору
«ЗНО не за горами» (завдання у форматі ЗНО)
Діагоналі паралелограма перетинаються в точці О (див. рисунок). Укажіть правильну векторну рівність.
ІІІ. Осмислення нового матеріалу.
Гра “Вірю – не вірю” (кожна правильна відповідь - 1 бал)
1. Вектор - будь-який відрізок (не вірю)
2. Нульового вектора не існує) (не вірю)
3. Вектори колініарні, якщо вони лежать на одній прямій або на паралельних прямих ) ( вірю)
4. Співнапрямлені вектори записуються так: ) (вірю)
5.Вектори називаваться рівними, якщо вони співнапрямлені (не вірю)
6. Два колінеарні вектори співнапрямлені ) (не вірю)
7. Нульовий вектор колінеарний будь-якому вектору (вірю)
Відповідь:
1. – 2.– 3.+ 4.+ 5.– 6. – 7. +
Самостійна робота (2 бали)
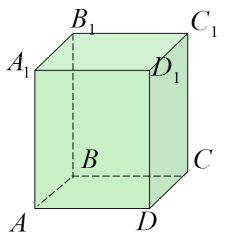
ABCDA1B1C1D1 паралелепіпед.
Укажіть вектор, початком і кінцем якого є вершини паралелепіпеда, що дорівнює:
+ + 
+ 
Відповідь: 
Самостійна робота (питання у форматі ЗНО) (3 бали)
У паралелограмі ABCD точка О – точка перетину діагоналей. Виразіть вектор 
через вектори
= і 
=
Відповідь:
VII. Підбиття підсумків уроку
- Роз’яснення незрозумілих питань.
- Самооцінювання робіт учнями.
- Оголошення оцінок за урок.
Твій настрій:
САМООЦІНКА: 
ОЦІНКА ВИКЛАДАЧА:
VIII. Домашнє завдання.
1) № 12.6 (початковий рівень)
№12.19 (середній рівень)
№ 12.23 (достатній рівень)
№ 12.29 (високий рівень)
2) Заповнити таблицю на стр. 2 робочого зошита
про публікацію авторської розробки
Додати розробку