Урок: " Відсоткові розрахунки"

                                                               Нестандартний урок                                                                                                                      Тема. Відсоткові розрахунки (11 КЛ. )      

Ванда Пашкова, учитель математики сш №196, м. Київ.

Мета уроку:

• Узагальнити знання учнів про відсотки, набуті в попередніх класах;
• Повторити основні типи й способи розв’язання задач на відсотки;
• Розвивати увагу, розумову діяльність, уміння виконувати порівняльний аналіз, спонукати до пізнавальної діяльності;
• Виховувати працьовитість, активність, інтерес до математики.

Тип уроку: узагальнення та систематизація знань.                           

 Обладнання та наочність: презентація у Power Point, конверти із завданнями, інтерактивна дошка, мікрофон, робочий зошит.

Епіграф

Той, хто хоче обмежитися сьогоднішнім без знань минулого, той ніколи його не зрозуміє…

                                                                                                                                      

                                                                                     Г. В. Лейбніц (1646-1716р.)

Хід уроку

 

І. Організаційний етап.         

     Учні класу об’єднуються у групи. (Відділ депозиту, відділ кредиту, відділ загальної інформації, відділ ризику, економічний відділ).

Учитель.

Перш ніж розпочати урок, я хочу звернути вашу увагу на слова, які сказав видатний математик Г.В.Лейбніц: "Той, хто хоче обмежитися сьогоднішнім без знань минулого, той ніколи його не зрозуміє…" Ці рядки залишаються актуальними і у наш час, тому що знання –це єдиний, цілісний нарозривний процес, який має початок,але не має кінця.

       

 II   Формування мети і завдань уроку.                                         

Мотивація навчальної діяльності учнів.

Учитель.

Він дві різні назви має,

Його бухгалтер поважає,

У бізнесі, торгівлі ─ всюди

З ним звикли справу мати люди.

Виконує він скрізь роботу,

А називається… (відсоток)

Сьогодні на уроці ми повторимо означення відсотків, основні типи і способи розв’язування задач на відсотки.

 

Колись класик української літератури М. Рильський сказав «Нове життя нового прагне слова». Я б додала, що не лише слова, а й дій, професій, нового мислення і світобачення в цілому. Щоб знайти застосування своїм здібностям  та можливостям, треба вміти швидко адаптуватись у сучасному життєвому просторі.  Скоро ви залишите стіни школи і перед вами постане гостро питання вибору професії. Мене цікавить, чи ви орієнтуєтесь, які професії зараз найбільш потрібні, як розвивається сучасний ринок праці.                                                                                   (Діти назвуть, швидше за все, професії економіста, юриста, фінансиста і т.д.).      ─ Звичайно, ви праві, ці професії дуже потрібні, бо саме вам належить підняти нашу економіку, зробити Україну процвітаючою державою. Тому сьогоднішній урок я хочу побудувати у вигляді ділової гри, яку так і назвемо «Банківська  справа».                                                                                                                                          Свій банк назвемо «Майбутнє України» ─ у вашу честь, бо ви ─ майбутні господарі української землі. От сьогодні ми й переконаємось, чи в надійних руках майбутнє нашої держави. Отже, розпочинаємо ділову гру. Як відомо, в Україні грошова одиниця ─ гривня (діти); у Європі ─ євро (діти), а ви будете отримувати за свої знання грошову одиницю «проценто», бо тема нашого уроку «Відсоткові   розрахунки.» Записали тему уроку.                                                                     До кінця уроку вам потрібно поповнити банк грошовою одиницею «проценто» у вигляді ваших знань.                                                                                                                                            Кожна нова справа, аби стати зрозумілою, повинна себе презентувати, тому ми проведемо сьогодні прес-конференцію для представників засобів масової інформації. Попрошу завідуючих відділами в кінці робочої години здати робочу документацію, щоб мені більш детально познайомитися з працівниками банку. III. Актуалізація опорних знань.

а) Відповіді на запитання журналістів.

1. Газета «Банківська справа»

─ У мене запитання до директора банку. Поясніть будь-ласка, що означає відсоток і кому приходиться часто розв’язувати задачі на відсотки.

2. Телепередача «Успішний бізнесмен»                                                        ─ Скажіть будь-ласка у яких операціях застосовується формула складних відсотків. Дякую.
3. Журнал «Історія і право»

─  Скажіть будь-ласка звідки пішла назва «відсоток»?                          

Символ % виник у XV столітті в Італії. Ще в XIII-XVI столітті всі підручники приділяли увагу відсотковому численню. Слово «процент» походить від латинського pro centum, що означає «від сотні», звідси і дві назви ─ процент і відсоток. Перші таблиці на відсотки склав Сімон Стевін-інженер з міста Брюсе (Нідерланди).

Відсотки застосовувались тільки в торгових і грошових угодах. Потім область їх застосування розширилась.             

Їх використовують для характеристики виконання виробничих планів, визначення зростання чи зниження продуктивності праці. У відсотках ми виражаємо вологість повітря, жирність молока, вміст солі у розчині, кількість відсутніх і присутніх учнів у класі. Зараз знання відсотка необхідне кожній людині.

4. Видавництво «Екзамен без проблем»

─ Які існують типи задач, навести приклади.

5. Газета «Банківська справа»

а) Як знайти на скільки відсотків число а > b. Навести приклади.

б) Як знайти на скільки відсотків b<a.       

6) Видавництво «Шпаргалка учнів» просить надати допомогу і пояснить, якими способами можна розв’язувати задачі на відсотки.                                                         7) Газета «Капітал»                                                                                                                                          а) Якщо деяка величина змінюється n разів на однакову величину відсотків кожного разу, яке значення цієї величини після n-ої зміни.                                                     б) А якщо ця величина змінюється кожного разу на різні величини відсотків, за якою формулою можна знайти значення після n-ої зміни.                                                        8) Газета «Банківська справа» а) Скільки відсотків становлять числа 0,28; 0,5; 0,248; 7. б) Скільки відсотків від однієї гривні становлять 4 копійки, 15 копійок, 60 копійок, 1 гривня, 7 гривень.                                                                                            9) Газета «Аргументи і факти»                                                                                                             Я хочу провести тестування всіх присутніх, щоб більше дізнатися про співробітників банку.

ТЕСТОВЕ ЗАВДАННЯ:

Варіант №1.   

1) Скільки кілограм солі міститься в 30кг 5%-го розчину?             А) 2; Б) 1,5; В) 3; Г) 2,5

2)30% деякого числа дорівнює 18. Знайти це число.                А) 90; Б) 48; В) 30; Г) 25

3) Скільки відсотків складає число 25 від числа 125?                 А) 10; Б) 15; В) 20; Г) 25

4) На скільки відсотків збільшиться периметр квадрата, якщо його сторону збільшити на 20%? А) 4; Б) 20; В) 2,2; Г)1

5) Протягом вересня 2009 р. ціна на сир «Гауда» зросла на 30%, а протягом жовтня 2009 р. ─ на 20%. На скільки відсотків піднялась ціна за 2 місяці. А)23; Б)28; В) 56; Г) 76

6) Фірма «Веселка» платить рекламним агентам 5% від вартості замовлення. На яку суму треба знайти замовлення, щоб одержати 2000 грн.                                    А) 10000; Б) 145; В) 456;Г) 40000

Варіант №2

1. Скільки кілограм солі міститься в 20кг 5%-го розчину?             А) 2; Б) 3; В) 1; Г)5
2. 20%  деякого числа дорівнює 18. Знайти  це число.           А) 90; Б) 40; В) 70; Г)10
3. Скільки відсотків складає число 30 від числа 120?               А) 15; Б) 20; В) 35; Г) 25
4. На скільки відсотків збільшиться периметр квадрата, якщо його сторону збільшити на 20%?                                                                                                                                          А) 25; Б) 20; В) 45; Г) 12
5. Протягом вересня 2009 р. ціна на сир «Гауда» зросла на 30%, а протягом жовтня 2009 р. ─ на 20%. На скільки відсотків піднялась ціна за 2 місяці. А) 43; Б) 23; В) 15; Г) 56
6. Фірма «Веселка» платить рекламним агентам 5% від вартості замовлення. На яку суму треба знайти замовлення, щоб одержати 3000 грн.                                       А) 1000; Б) 235; В) 40000; Г) 60000

Варіант №3

1. Скільки кілограм солі міститься в 10кг 5%-го розчину?            А) 0,5; Б) 23; В)1; Г)4,5
2. 25% деякого числа дорівнює 20. Знайти це число.               А) 20;Б) 80; В) 21; Г) 56
3. Скільки відсотків складає число 40 від числа 160?                А) 21; Б) 24; В) 5; Г) 25
4. На скільки відсотків збільшиться периметр квадрата, якщо його сторону збільшити на 20%?                                                                                                                                        А) 12; Б) 56; В) 71; Г) 20
5. Протягом вересня 2009 р. ціна на сир «Гауда» зросла на 30%, а протягом жовтня 2009 р. ─ на 20%. На скільки відсотків піднялась ціна за 2 місяці. А) 45; Б) 56; В) 67; Г) 32
6. Фірма «Веселка» платить рекламним агентам 3% від вартості замовлення. На яку суму треба знайти замовлення, щоб одержати 3000 грн. А) 123; Б) 100000; В) 200000; Г) 1500

Варіант №4    

1. Скільки кілограм солі міститься в 30кг 2%-го розчину?            А) 1; Б) 2; В)3; Г)0,6
2. 20% деякого числа дорівнює 50. Знайти це число.               А) 250;Б) 150; В) 20; Г) 12
3. Скільки відсотків складає число 40 від числа 200?                А) 3; Б) 20; В) 30; Г) 48
4. На скільки відсотків збільшиться периметр квадрата, якщо його сторону збільшити на 20%?                                                                                                                                        А) 10; Б) 20; В) 25; Г) 13
5. Протягом вересня 2009 р. ціна на сир «Гауда» зросла на 30%, а протягом жовтня 2009 р. ─ на 20%. На скільки відсотків піднялась ціна за 2 місяці. А) 56; Б) 66; В) 46; Г) 13
6. Фірма «Веселка» платить рекламним агентам 3% від вартості замовлення. На яку суму треба знайти замовлення, щоб одержати 1200 грн. А) 30000; Б) 234; В) 645; Г) 40000

Варіант №5

1. Скільки кілограм солі міститься в 20кг 4%-го розчину?            А) 0,8; Б) 1; В)2; Г)4,2
2. 30% деякого числа дорівнює 15. Знайти це число.               А) 20;Б) 21; В) 40; Г) 50
3. Скільки відсотків складає число 30 від числа 150?                А) 20; Б) 13; В) 16; Г) 30
4. На скільки відсотків збільшиться периметр квадрата, якщо його сторону збільшити на 20%?                                                                                                                                        А) 10; Б) 30; В) 50; Г) 20
5. Протягом вересня 2009 р. ціна на сир «Гауда» зросла на 30%, а протягом жовтня 2009 р. ─ на 20%. На скільки відсотків піднялась ціна за 2 місяці. А) 46; Б) 23; В) 56; Г) 34
6. Фірма «Веселка» платить рекламним агентам 2% від вартості замовлення. На яку суму треба знайти замовлення, щоб одержати 2000 грн. А) 100000; Б) 200; В) 457; Г) 20000

Варіант №6

1. Скільки кілограм солі міститься в 30кг 3%-го розчину?            А) 1,2; Б) 0,9; В)3,1; Г) 23
2. 30% деякого числа дорівнює 18. Знайти це число.               А) 30;Б) 13; В) 40; Г) 60
3. Скільки відсотків складає число 30 від числа 300?                А) 10; Б) 22; В) 20; Г) 30
4. На скільки відсотків збільшиться периметр квадрата, якщо його сторону збільшити на 20%?                                                                                                                                        А) 10; Б) 20; В) 30; Г) 23
5. Протягом вересня 2009 р. ціна на сир «Гауда» зросла на 30%, а протягом жовтня 2009 р. ─ на 20%. На скільки відсотків піднялась ціна за 2 місяці. А) 57; Б) 23; В) 56; Г) 11
6. Фірма «Веселка» платить рекламним агентам 5% від вартості замовлення. На яку суму треба знайти замовлення, щоб одержати 1000 грн. А) 20000; Б) 234; В) 10000; Г) 5000

Варіант №7

1. Скільки кілограм солі міститься в 20кг 4%-го розчину?            А) 0,8; Б) 0,7; В)12; Г)45
2. 20% деякого числа дорівнює 40. Знайти це число.               А) 100;Б) 200; В) 300; Г) 56
3. Скільки відсотків складає число 25від числа 50?                А) 20; Б) 40; В) 50; Г) 12
4. На скільки відсотків збільшиться периметр квадрата, якщо його сторону збільшити на 20%?                                                                                                                                        А) 10; Б) 20; В) 30; Г) 80
5. Протягом вересня 2009 р. ціна на сир «Гауда» зросла на 30%, а протягом жовтня 2009 р. ─ на 20%. На скільки відсотків піднялась ціна за 2 місяці. А) 23; Б) 46; В) 67; Г) 56
6. Фірма «Веселка» платить рекламним агентам 5% від вартості замовлення. На яку суму треба знайти замовлення, щоб одержати 2000 грн.                           А) 10000; Б) 2000; В) 30000; Г) 40000

Листи з розв’язками учні здають бухгалтеру, а бланки з відповідями залишають у себе.

Учитель. Повторення теоретичного матеріалу. Перевіримо наскільки правильну інформацію ви дали представникові газети «Аргументи і факти».

Перевіримо розв’язки задач  варіанта №1 (завдання з розв’язками спроектовані на інтерактивну дошку).

Варіант №1

1. Скільки кілограм солі міститься в 30 кг 5%-го розчину?

30*0,5=1,5 (кг)

     А)2; Б) 1,5; В) 3; Г) 2,5

2) 30% деякого числа дорівнює 18. Знайти це число.

     18/30*100=60

     А) 90; Б) 48; В) 30; Г) 60

3)  Скільки відсотків складає число 25 від числа 125?

     25/125*100%=20%

     А) 10; Б) 15; В) 20; Г) 25

4) На скільки відсотків збільшиться периметр квадрата, якщо його сторону збільшити на 20%?

       1,2*а=4,8а; а – сторона квадрата

       (4,8а-4а)/4а= 0,8а/4а=0,2 (20%)

5. Протягом вересня 2009 року ціна на сир «Гауда» зросла на 30%, а протягом жовтня 2009 року – на 20%.  На скільки відсотків піднялася ціна за два місяці.

Х*1,3*1,2=1,56х(56%).

6. Фірма «Веселка» платить рекламним агентам 5% від вартості замовлення. На яку суму треба знайти замовлення, щоб одержати 2000 грн.

2000/5*100=40000 (грн.)

Отримані відповіді відмітити в бланку, а розв’язки задач здати бухгалтеру.

 

	а	б	в	г
1
2
3
4
5
6

 

Після перегляду розв’язку задач відповіді до тестів  спроектовано на екран.  Учні перевіряють розв’язки завдань.

 

	1	2	3	4	5	6
В-1	1,5 (Б)	60 (Г)	20 (В)	20  (Б)	56 (В)	40000 (Г)
В-2	1     (В)	90 (А)	25 (Г)	20 (Б)	56 (Г)	60000 (А)
В-3	0, 5 (А)	80 (Б)	25 (Г)	20 (Г)	56 (Б)	100000 (Б)
В-4	0,6 (Г)	250 (А)	20 (Б)	20 (Б)	56 (А)	40000 (Г)
В-5	0,8 (А)	50 (Г)	20 (А)	20 (Г)	56 (В)	100000 (А)
В-6	0, 9 (Б)	60 (Г)	10 % (А)	20 (Б)	56 (В)	20000 (А)
В-7	0,8 (А)	200 (Г)	50 % (В)	20 (Б)	56 (Г)	40000(Г)

 

А зараз перевіримо, наскільки ви дали вірну інформацію представнику газети «Журнали і факти».

Якщо учні допустили в якомусь завданні помилки, ще раз розглянути розв’язок завдання  в якому допущені помилки.

Учитель.  Підніміть руки, хто виконав тести на 12 проценто? (Кожне завдання оцінюється у 2 проценто.) Хто на 10 проценто? Хто на 8 проценто? Хто отримав менше   8 проценто? Оскільки учні не отримали  нижче за 8 проценто, то слова учителя: « Тести показали, що економіка України в надійних руках.»

 

 

 

б)Усне виконання вправ.

9) Телепередача «Віриш не віриш»

1. Розчин містить 4% солі. Скільки грамів солі міститься в 350 г розчину?

350*0,4=140 (г)

Відповідь: не вірю, бо 4%=0,04, тому 350*0,04=14(грам)

2. На скільки відсотків число 27>25?

(27-25)/25*100%=8%

Відповідь:вірю.

3. На скільки відсотків число 5<20?

(20-5)/20*100%=15*5%=75%

Відповідь: вірю.

 

4. Вартість товару понижалась на 10%, потім на 20% і на 30%. Як змінилась ціна товару?

х*0,1*0,8*0,7=0,056х, х- початкова ціна товару, 0,056=5,6%. Отже, ціна товару зменшилася на 94,4% ,бо 100%-5,6%=94,4%.

Відповідь: не вірю, бо застосувавши загальний вигляд формули складних процентів будемо мати: х*0,9*0,8*0,7=0,504х (50,4%). Тоді 100%-50,4%=49,6%. Отже, початкова ціна знизилась на 49,6%.   

5. Розгадайте кросворд.

 

Розшифрувати назву міста:
1	Чверть	66%	С
2	Приблизно третина	20%	Е
3	Половина	50%	Л
4	П’ята частина	25%	В
5	Чотири п’ятих	80%	Н
6	Три чверті	33%	А
7	Приблизно дві третини	75%	І
8	Одна десята	10%	Я

 

Розшифрувати назву міста:
1	Чверть	25%	В
2	Приблизно третина	33%	А
3	Половина	50%	Л
4	П’ята частина	20%	Е
5	Чотири п’ятих	80%	Н
6	Приблизно дві третини	66%	С
7	Три чверті	75%	І
8	Одна десята	10%	Я

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Який відсоток площі Києва становить площа Андорри?

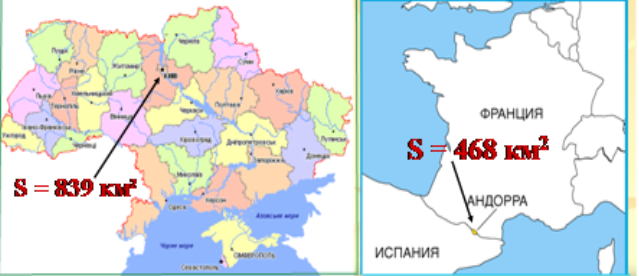
 Відповідь:40%. Так чи ні?

 Відповідь учнів: ні, бо ·100% ≠ 40%.

 Учитель:

1. В кав’ярні шоколад коштує 4 грн., а його закупівельна ціна становить 3,2 грн. Скільки відсотків становить націнка?

Розв’язання

          Складемо пропорцію:

          3,2 – 100%

          4   -   х%.

          3,2·х%=400%,

          х=125%.

          Націнка становить 125%-100%=25%.

          Відповідь:25%.

 

2. Якщо ціна понижається на 10%, 20%, 30%. За якою формулою можна  знайти зміну початкової величини товару?

Відповідь:  Застосувати  загальний  вигляд формули складних процентів.

3. Населення міста за три роки зросло з 200 000 до 231525 чоловік. За якою формулою можна знайти середньорічний відсоток зростання населення?

Відповідь: За формулою складних процентів.

 

Учитель.

Чи є ще питання у журналістів?

Газета «Сільські вісті»

Якщо ціну на цукор підвищили на 20%, а потім знизили на 20 %, то чи отримаємо знову початкову ціну?

Учитель.

Наприклад. Ціна 1 кг. цукру становила 10 грн., ціну підвищили на 20%, а потім знизили на 20%. Яка тепер стала ціна одного кілограма цукру?

Розв’язання

Оскільки першого разу ціну підвищили на 20%, то ціна стала 10·1,2=12(грн.). Другий раз знизили на 20%, тому ціна стала 12·0,8=9,6(грн.).

Відповідь: Початкову ціну не отримаємо.

 

       Іv Застосування знань, умінь та навичок.

 

Виконання письмових вправ.

Оскільки поступило замовлення, то зараз усі працівники  відділів будуть готувати відповіді на запитання клієнтів. Робочу документацію ви повинні надати в найближчий час

̀Відділ депозиту

1. Вкладник поклав до банку на 2 різні рахунки 1200 грн. За 1-ий рахунок банк виплачує 6% річних, а за 2-ий 8 % річних. Через рік клієнт отримав 80 грн відсоткових грошей. Скільки гривень він поклав на кожен рахунок?
2. Вкладник відкрив рахунок у банку, внісши 2 000 грн. на вклад під  12% річних, за схемою приєднання нарахованих відсотків до  тіла внеску через рік. Скільки грошей буде на його рахунку через 3 роки?

Розв’язання

1)  Нехай  х грн.- сума, що була покладена на перший рахунок, тоді на             другий рахунок було покладено 1200-х грн., 0,06 грн.- нараховані гроші за перший рахунок і (1200-х)·0,08грн.- нараховані гроші за другий рахунок. Отже, враховуючи умову задачі маємо:

0,06х+(1200-х)·0,08=80; 0,06х+96-0,08х=80; 0,02х=16; х=800грн.;

1200-800=400(грн.)

Відповідь: 800грн. покладено на перший рахунок і 400грн. на другий рахунок.

2)   Застосуємо формулу складних процентів:

2000·(1,12)=2000·1,404928=2809,856.

Відповідь:2809грн.86коп. буде на його рахунку через 3 роки.

                     

 

 

Відділ кредиту

1. Перед кризою дехто взяв у кредит на 5 років 50 000$  США під 8% річних, під заставу квартири, яка коштувала 60 000$ США на той час. Квартира подешевшала на 20%. Протягом 5 років гроші не вносилися в рахунок погашення кредиту. Яку суму буде винен позичальник кредитній установі у разу продажу банку застави у вигляді квартири?
2. У результаті інфляції у державі ціни зросли на 150%. Дума зажадала від уряду повернення цін до попереднього рівня. На скільки відсотків повинні бути зменшені ціни?

Розв’язання

1. 60000·0,8=48000($) стала коштувати квартира після того як вона подешевшала. 50000·(1,08)=73466,4($)- винен позичальник кредитній установі через 5 років. 73466,4-48000=25466,4($)- залишиться винен позичальник  кредитній установі у разі продажу банку застави у вигляді квартири.

    Відповідь: Залишиться винен 25466,4$.

2. Нехай х – початкова ціна товару. Після інфляції ціна стала 2,5х, а

    р% - шукана знижка .Враховуючи умову задачі складемо рівняння:

2,5х·(1-  )=х;                                            р=60%.

Відповідь: ціну потрібно знизить на 60%.

 

Відділ загальної інформації

1. Змішали 30%-ий розчин борної кислоти з 15%-им розчином і отримали 450 гр. 20% розчину. Скільки грамів кожного розчину треба взяти?
2. Є сплав міді з оловом вагою 12кг, який містить 45% міді. Скільки чистого олова потрібно добавить до цього сплаву,щоб сплав мав 40% міді%?

Розв’язання

1. Нехай 30% - го розчину взято х грамів, тоді 15% --го розчину взято 450-х грамів. Оскільки перший розчин 30%, то в х грамах цього розчину міститься 0,3х грамів кислоти, а в 450-х грамах 15%-го розчину міститься

(450-х)·0,15грамів кислоти. В отриманій суміші за умовою задачі міститься

450·0,2=90(грамів) кислоти. Отже, маємо рівняння:

0,3х+(450-х)·0,15=90; 0,15х=22,5; х=150грамів взято 30% розчину,

450-150=300(грамів) взято 15% розчину.

Відповідь: 150грамів і 300грамів.

2. Нехай потрібно добавити х кг олова до цього сплаву. Тоді вага сплаву буде 12+х кг.

Визначимо кількість міді вданому сплаві: 12·0,45=5,4(кг). Оскільки кількість міді  в сплаві не змінюється, то маємо рівняння:

(12+х)·0,4=5,4х=1,5кг.

Відповідь: потрібно добавити до сплаву 1,5кг чистого олова.

      

 

    

 

Відділ ризику

1. Свіжі гриби містять за масою 90% води, а сухі  - 12%. Скільки вийде сухих грибів з 22 кг свіжих? Які гриби вигідніше продати, якщо ціна свіжих – 50 грн. за 1 кг, а ціна сухих 300 грн. за 1 кг?
2. Є два сплави міді і цинку. В першому сплаві міді в два рази більше ніж цинку, а в другому міді в 5 раз менше, ніж цинку. У скільки разів треба взяти другого сплаву більше ніж першого, щоб одержати новий сплав в якому цинку в два рази більше ніж міді?

Розв’язання

1. Знайдемо скільки кг безводної маси знаходиться у 22 кг свіжих грибів.

  22·0,1=2,2кг.

2,2кг складає  88% сухих грибів, тоді 0,88·х=2,2;  х=2,5кг вийде сухих грибів з 22 кг свіжих.

22·50=1100(грн.) - ціна свіжих грибів.

2,5·300=750(грн..) –ціна сухих грибів.

Відповідь: 2,5кг.; вигідніше продати свіжі гриби.

2. Нехай маса першого сплаву х кг, а маса другого сплаву у кг. Складемо таблицю.

Сплав	Маса сплаву в кг	Вміст міді,кг	Вміст цинку,кг
І	х	х	х
ІІ	у	у	у
Новий сплав	х+у	(х+у)	(х+у)

Усього частин у першому сплаві 3, а в другому- 6, отже в першому сплаві міді , а у другому – . Аналогічно цинку першому сплаві, а в другому В новому сплаві міді ,а цинку . Отже маємо рівняння:

х+у=(х+у);   4х+у=2х+2у; 2х=у; у=2х.

Відповідь: другого сплаву треба взяти у 2 рази більше за перший.  

 

 

Економічний відділ

1. Холодильник вміщує не більше 320 кг сиру. Чи можна купити 1 т молока жирність якого становить 5%, з  якого виготовляють сир жирністю 15, 5 відсотка і при цьому залишається сироватка жирністю 0,5 %, щоб весь сир можна було помістити у холодильник?
2. Ціну товару знижували двічі на однакове число відсотків, у результаті чого його вартість склала 64% від початкової. На скільки відсотків кожного разу знижувалась ціна?

Розв’язання

             1) Знайдемо скільки жиру міститься в 1 т молока: 1000·0,05= 50кг.

              Нехай в 1т молока міститься х кг сиру і у кг сироватки. Отже маємо 

               перше рівняння системи:

              х+у=1000.

              Жиру у сирі 0,155х кг, а у сироватці – 0,005у кг. Оскільки всього жиру   

              50кг, то маємо друге рівняння системи: 

               0,155х+0,005у=50.

              2)Нехай х(х≠0) –початкова ціна товару,  р%- шукана знижка. Ціна товару

                після першої знижки  стала х·(1-0,01р), після другої знижки-

                 х·(1-0,01) .

                Оскільки ця ціна склала 64% від початкової, а саме 0,64х, то маємо

                рівняння: х·(1-0,01р)=0,64х. (1-0,01р)=0,64; 1-0,01р=0,8; 0,01р=0,2;

                р=20%.

                Відповідь: на 20% кожного разу знижувалась ціна.

             

 

 

Біля дошки після виконання завдань кожний відділ захищає свій спосіб розв’язування задач, інші доповнюють. Першу задачу із відділу кредиту пояснює директор банку.

 

Учитель: Для чого людині потрібні знання?

Є біблійна притча, яка лежить в основі оповідання Л. Толстого «Много ли земли нужно человеку?». Селянину Пахому продають землю по ціні «1000 рублей за день». Під цим потрібно розуміти ту кількість землі, яку він зможе обійти за день. Автор висміює людину – скнару, але більшою мірою його невігластво. Якби Пахом знав, що серед усіх прямокутників даного периметра найбільшу площу має квадрат, то оббіг би хоча би один квадрат.

А в оповідання Пахом біг цілий день по прямій і під кінець дня впав мертвий. Таке невігластво може мати плачевні результати. Пам’ятайте про це завжди. Недаремно ж кажуть, що «світом править той, хто володіє інформацією»…

Щодня у світі розв’язується нескінченна кількість задач на обчислення площі і розв’язування задач на відсотки та проблем, що пов’язані з ними, і їх розв’язання залежить від глибини знань людини.

Скоро ви закінчите школу, хтось із вас стане економістом, хтось  бухгалтером, менеджером, фермером, підприємцем і т.д., щодня доведеться розв’язувати задачі на відсотки, та якщо хтось і не буде мати жодної з цих професій, все одно, хоч інколи, але доведеться мати справу із відсотками. Я впевнена, що ті уроки, які були проведені з даної теми, не пройдуть безслідно, і ви на все життя запам’ятаєте основні типи і способи розв’язування таких задач.

І запам’ятайте:

 

Числа

правлять світом!  

Піфагор

 

 

Підсумок уроку.

Вчитель.

• На уроці ви добре працювали, продемонстрували знання, активність, добре мислили.

А тепер давайте оцінимо вашу роботу на уроці.

Що було вдалим і чому?

З якими труднощами ви зустрілися? Що допомогло подолати труднощі? Чого навчилися під час уроку?

Оцінювання учнів (підраховується кількість грошової одиниці «проценто», яку кожен учень набрав за урок).

Домашнє завдання.

Радіопередача «Роблю сам»

Самостійно вдома скласти задачі, які можна розв’язати:

а) використовуючи таблицю,

б) за допомогою формули складних процентів,

в) застосовуючи загальний вигляд формули складних процентів,

г) за допомогою формули простого відсотка.

Додаток.

Таблиця оцінювання учнів у проценто (заповнює бухгалтер).

№	П.І.учня	Відповіді на запитання журналістів (9 або менше)	Тестове завдання (12)	Усне виконання вправ (6)	Письмове виконання вправ (6)	Разом
1
…

 

Шкала переведення проценто в оцінку

Бали	0-5	6-9	10-11	12-15	16-19	20-23	24-27	28-29	30-31	32-33
Оцінка	3	4	5	6	7	8	9	10	11	12

Література

1.Бевз Г. П. Алгебра: підручник для 9 класу загальноосвіт. навч. закл. /

Г.П. Бевз, В.Г.Бевз.- К.: Зодіак-ЕКО, 2009..—288с.: іл.

2. МерзлякА.Г., Полонський Б.Б.,  ЯкірМ.С.   Збірник завдань для державної підсумкової атестації з математики: 9 кл.—Х. Гімназія,2016.

3. Методи розв’язування задач з математики: у 2-хкнигах– 4частинах.Книга 2.– Частина ІІІ, ІV: навчально-методичний посібник для учнів загальноосвітніх закладів, шкіл, ліцеїв і шімпазій з поглибленим вивченням математики та абітурієнтів /В.П.Лісовська, Т.О.Зінькевич, Н.С.Чепурна, Н.П.Щекань.–Камянець-Подільський: Аксіома,2010.–416с.