Урок "Відсоткові розрахунки" 9 клас

Урок – симпозіум у 9 класі з алгебри на тему:

«Відсоткові розрахунки. Формула складних відсотків»

Мета уроку: узагальнити і систематизувати знання, вміння і навики учнів розв'язувати задачі на відсотки, показати на прикладах практичну спрямованість математичних знань, забезпечити політехнічну підготовку і профорієнтацію учнів, сприяти формуванню економічної грамотності, моральних і ділових якостей учнів; розвивати пам'ять, логічне мислення; мовлення учнів, викликати інтерес до навчання; інтеграція та застосування знань на практиці; розвиток самостійності та пізнавальної діяльності

 

Вид уроку: нетрадиційний, урок-симпозіум

 Тип уроку:  урок формування і вдосконалення вмінь та навичок.

 Обладнання: роздатковий матеріал для груп, проектор, комп’ютер

Епіграф  уроку

Немає жодної галузі математики,

якою б абстрактною вона не була,щоби її

коли-небудь не виявилося  застосованою

для явищ дійсного світу

М. І. Лобачевський

Хід уроку

І. Повідомлення теми і мети уроку

Відеорепортаж

• Добридень! Говорить Городниця ТV. Сьогодні у примищенні школи відбувається незвичайна подія. З’їзд учених різних галузей науки, техніки і сільського господарства. Що привело їх сьогодні до нас.
• Представтися хто ви і чому ви завітали до нас?
• Ми представники хімічної промисловості , нам необхідна допомога математиків у вирішенні деяких проблем. Ми просимо допомоги математиків у розв’язанні задач  на суміші і сплави.
• А ви хто і на що сподіваєтеся?
•  Ми представники банківської сфери нам потрібно вирішити проблему нарахування відсотків клієнтам.
• А ми представники сільського господарства. Нам теж потрібна допомога математики.
• І ми представники кулінарії сподіваємося на вирішення наших проблем.

- Як бачимо гості все прибувають і прибувають і всі вони мають єдину мету. Вони сподіваються, що наука математика допоможе їм розвязати задачі практичного характеру, повязані із відсотками. Що ж слідкуймо за новинами. Дивімося, як математика служить іншим наукам, як допомагає їм. Адже Лобачевский сказав:

 Немає жодної галузі математики,

якою б абстрактною вона не була,щоби її

коли-небудь не виявилося  застосованою

для явищ дійсного світу.

• Залишайтеся з нами. З вами була  ваша Олена Шевчук.

 

Вчитель:

• Розпочинаємо роботу нашого математичного симпозіуму. Зустрічайте.

Представники банківської сфери.

Представники хімічної промисловості.

Представники сільського господарства,  кулінарії.

Представники Підприємницької діяльності

Істориків.

ІІ. Перевірка домашнього завдання

Шановні  члени математичного симпозіуму вітаємо вас у стінах нашого класу. Сподіваємося на плідну співпрацю і взаємодопомогу. Нас зібрали сюди задачі на відсоткові розрахунки. За допомогою сьогоднішнього уроку ми побачимо практичне застосування відсотків, покажемо як їх використовують у різних галузях.

Щоб настроїтися на розв’язування наших проблем пропоную розв’язати тести.

Тест з теми «Відсотки»
1) 1% від числа – це
а) десята частина числа; б) тисячна частина числа;
в) сота частина числа; г) друга частина числа.
2) Для того, щоб знайти k % від числа А, треба
а) число А поділити на 100;
б) число А поділити на k;
в) число А поділити на 100 і помножити на k;
г) число А поділити на k і помножити на 100.
3) Для того, щоб знайти невідоме число Х, якщо k% від нього дорівнює А,
треба
а) число А поділити на 100;
б) число А поділити на k;
в) число А поділити на 100 і помножити на k;
г) число А поділити на k і помножити на 100.
4) Для того, щоб знайти, скільки відсотків число А складає від N, треба
а) число N поділити на 100;
б) число А поділити на 100;
в) число А поділити на N;
г) число А поділити на N і помножити на 100%.
5) Висадили 300 зерен, з яких 270 зійшли. Який відсоток становлять зерна,
що не дали сходів?
а) 90% б) 10 % в) 27% г) 30%
6) На склад завезли 95 т капусти. 20% всієї капусти відправили в магазин.
Скільки тон капусти залишилось на складі?
а) 76т б) 25т в) 80т г) 19т
7) Із пшениці отримують 40% борошна. Скільки борошна отримують із 260т
пшениці?
а) 104% б) 130т в) 650т г) 640т
8) 8% шляху складають 48км. Чому дорівнює довжина всього шляху?
а) 504 км б) 600км в) 700км г) 240км
9) Яблука містять 12% цукру. Скільки цукру міститься в 30 ц яблук?
а) 3,6ц б) 3,4ц в) 3,2ц г) 2,4ц
10) При виготовленні пюре із слив 28% іде у відходи. Скільки треба взяти
слив, щоб отримати 28,8 т пюре?
а) 36т б) 42т в) 30т г) 40т
11) При виготовленні силосу ( їжа для рогатої худоби) втрачається 12%
закладеної зеленої маси. Скільки силосу буде отримано із 350т зеленої
маси?
а) 380т б) 312т в) 308т г) 310т
12) Сторони прямокутника 30см і 40см. Кожну із сторін збільшили на
20 %. На скільки відсотків збільшилась площа прямокутника?
а) 20% б) 40% в) 42% г) 44%

Правильні відповіді на екрані. Панове оцінюємо рівень наших досягнень.

Самооцінка.

ІІІ.  Актуалізація опорних знань

До доповіді запрошуємо істориків.

Процент (відсоток) - від латинського слова “pro centum” – сота частина

Слово «відсоток» походить від латинського pro centum, що буквально означає «за сотню» або «зі ста». Відсотками дуже зручно користуватися на практиці, так як вони виражають цілі частини чисел в одних і тих же сотих частках. Знак «%» походить, як вважають, від італійського слова cento (сто), яке в процентних розрахунках часто писалося скорочено cto. Існує й інша версія виникнення цього знака. Передбачається, що цей знак стався в результаті безглуздої помилки, вчиненої складачем. У 1685 році в Парижі була опублікована книга - керівництво по комерційній арифметиці, де помилково складач замість cto ввів %.

Вперше опублікував таблиці для розрахунку відсотків в 1584 році Симон Стевін - інженер з міста Брюгге (Нідерланди).

Відсотки застосовувалися тільки в торгових і грошових угодах. Потім область їх застосування розширилася, відсотки зустрічаються в господарських і фінансових розрахунках, статистиці, науці і техніці. Нині відсоток - це приватний вид десяткових дробів, сота частка цілого (прийнятого за одиницю).

Згадаймо основні типи задач на відсотки.

• Знаходження відсотків від числа.
• Знаходження числа за його відсотком
• Знаходження відсоткового відношення двох чисел
• Поняття складних відсотків
•      Як знаходимо відсотки від даного числа?
•       
•      Щоб знайти р % від даного числа а, достатньо це число поділити на 100 і помножити на число відсотків, тобто:
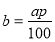
• де 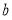— число, що дорівнює р % від числа 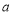. Або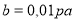 

 

Приклад 1

• Завод випускає 300 виробів за місяць. На скільки виробів за місяць збільшиться випуск продукції, якщо продуктивність праці збільшиться на 20 %?
• Розв'язання
• .
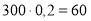• Відповідь. На 60 виробів.

 

 

• Як знайти число за його відсотками ?
•  

(Щоб знайти невідоме число , р % якого становить число , достатньо число помножити на 100 і одержаний добуток поділити на р,тобто:

)

• Приклад 2
• У результаті збільшення продуктивності праці на 15 % завод виготовляє 920 виробів за місяць. Скільки виробів протягом місяця виготовляв завод раніше?
• Розв'язання
• Оскільки продуктивність праці збільшилася на 15 %, то 920 виробів становлять 115 %. Задача зводиться до відшукання числа за відсотком:  920:1,15 = 800.
• Відповідь. 800 виробів.
•  
• Як розв’язуємо задачі на знаходження відсоткового відношення двох чисел?
•  

(Щоб знайти відсоткове відношення числа до числа а, достатньо знайти їх відношення і помножити на 100 %:

• )

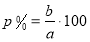Приклад 3

• Завод випускав 852 вироби за місяць. У результаті технічного переоснащення він став випускати 1136 виробів за місяць. На скільки відсотків збільшилася продуктивність праці?
• Розв'язання
• Випуск продукції збільшився на 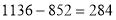(вироби).
• Отже, задача зводиться до відшукання відсоткового відношення чисел 284 і 852, тобто
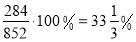
• Відповідь. Продуктивність праці збільшилася на 33- %.
•  

 

ІV. Розв’язування задач.

Прослухаймо доповіді представників банківської сфери

Банкіри

• Поняття складних відсотків найбільш поширене у нашій сфері
•  
• На практиці часто зустрічаються задачі, у яких доводиться обчислювати відсотки величин, одержаних у результаті нарахування відсотків. Це можна зробити за формулою:
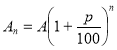
• де А — це вихідне число, на яке нараховуються відсотки р,п — кількість нарахувань.
• Ця формула називається формулою складних відсотків.

 

• Приклад 4
• Вкладник поклав у банк 200 000 гри під 7 % річних. Які відсоткові гроші він одержить через 5 років?
• Розв'язання.
• За умовою початкова сума поетапне змінюється. При цьому кожного разу її зміна становить певну кількість відсотків від значення, яке ця величина мала на попередньому етапі. Нехай 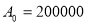грн — вихідне значення, яке змінюється на сталу кількість р % і п разів, де р =7; п= 5, тоді
• .
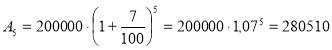• Відсоткові гроші: 280 510 - 200 000 = 80 510.
• Відповідь. 80 510 грн.

 

 

Пропонуємо вашій увазі розв’язати ось такі задачі. Їх результати стануть ще й відомими датами у біографії відомого українця, а хто він ми довідаємося розв’язавши їх, кожна задача - 4 бали

Задача 1.

Вкладник поклав у банк 665 грн під 7 % річних. Який прибуток він отримає через рік ?

Розв’язок розкаже скільки років прожила ця людина

Задача  2

Вкладник поклав до банку 1440грн під 8% річних. Скільки  грошей буде в нього на рахунку через 3 роки?

Розв’язок вкаже на рік народження даної людини.

Задача 3

Скільки грошей поклав вкладник до банку під 12% річних, якщо через 2 роки на його рахунку стало 2335 гривень?

Результат вкаже коли дана людина пішла із життя.

І так що ми одержали

• Дана людина прожила 47 років,
• Народилася у 1814р.
• Померла у 1861році.

Про кого розповідають нам ці числа? Так саме про Т.Г.Шевченка – відомого поета, художника,громадського діяча, патріота. Цього року ми відзначаємо 200-річчя з дня його народження. Вірші Шевченка впродовж століть залишаються актуальними. Його заповіти є незмінними для нас.

 

Вчитель

Запрошуємо до слова представників хімічної промисловості

 Основними в нашій науці задачі, де використовується поняття відсоткових розрахунків є задачі на суміші і сплави

При розв’язування цих задач доводиться користуватися поняттями «концентрація», процентний вміст», проба».

Будемо вважати, що всі розчини, суміші, сплави однорідні.

Процентною концентрацією речовини називається відношення маси розчиненої речовини до маси всього розчину, виражене у відсотках. , де m – маса розчину, q – маса розчиненої речовини.

При складанні рівняння обчислюється вміст якої-небудь однієї речовини в суміші, сплаві.

Вміст коштовних металів у сплавах виражається пробою. Пропонуємо вам задачу, яку ми розв’язали самостійно вдома.

Приклад 5.

У лабораторії є суміш, загальна маса якої на 3,3 кг більша від маси титану, що міститься у ній. Якщо добавити до неї 2 кг суміші з 25 % вмісту титану, одержимо суміш, у якій 20 % титану. Визначити початкову масу суміші і відсоток титану в ній.

Розв'язання

Нехай m кг – початкова маса суміші, х % – вміст у ній титану.

Тоді 0,01mx кг – маса титану в суміші.У 2 кг нової суміші маса титану дорівнює

2* 0,25 = 0,5 (кг).

Загальна маса титану при змішуванні сумішей становитиме (0,01mx+0,5) кг, а загальна маса змішаних сумішей (m+2) кг. Складаємо систему рівнянь:

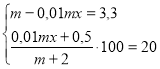
Розв’язавши систему маємо ,

Відповідь. 4 кг, 17,5 %.

Дорогі колеги пропонуємо вам  допомогти розв’язати нам такі задачі

Клас ділимо на 3 групи і розв’язуємо задачі. Кожна задача оцінюється у 4 бали

Задача 1

Обчислити масу і пробу сплаву срібла з міддю, знаючи, що при сплавленні його з 3 кг чистого срібла можна одержати сплав 900-ї проби, а при сплавленні його з 2 кг сплаву 900- ї проби — сплав 840-ї проби.

Розв'язання

Нехай сплав містить х кг срібла і у кг міді. При сплавленні цього сплаву з 3 кг чистого срібла маємо (х+3) кг – маса срібла, (х+у+3) кг – загальна маса сплаву. Відношення маси чистого металу до загальної маси сплаву – це проба, яка за умовою є 900-ю, що у частинах дорівнює 0,9. Тому

Аналогічно одержуємо друге рівняння:

Після спрощення рівнянь маємо систему:

   

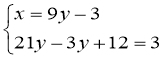
– маса сплаву.     – проба сплаву.

Відповідь. 3 кг 800-ї проби.

Задача 2

Скільки золота 600-ї та 900-ї проб потрібно сплавити, щоб одержати 350г золота 720-ї проби?

Розв'язання

Нагадаємо, що золото 600-ї проби – сплав, 1000 г якого містять 600 г чистого золота; золото 900-ї проби – сплав, 1000 г якого містять 900 г чистого золота.

Нехай першого сплаву взяли х г, другого – у г,тоді .

0,6х і 0,9у – вміст чистого золота у першому і другому сплавах відповідно. У 350 г нового сплаву міститься золота (г), тоді

Розв'язуємо систему:

Відповідь. 210 г золота 600-ї проби, 140 г золота 900-ї проби.

Задача 3

До розчину, що містить 40 кг солі, додали 200 кг води, після чого його концентрація зменшилася на 10 %. Скільки води містив початковий розчин і яка була концентрація?

Розв'язання

Нехай х кг води містить початковий розчин, тоді відсотковий вміст солі (концентрація) у ньому становить

кг – маса нового розчину, а – його концентрація, яка за умовою задачі менша на 10 % від концентрації початкового розчину. Отже, маємо рівняння:

   – не задовольняє умову задачі. Отже; початковий розчин містить 160 кг води. Знайдемо його концентрацію: 

Відповідь. 160 кг, 20 %.

Економіка                           

Відсоткові розрахунки використовуються у розв’язуванні задач економіки. Ще задачі на визначення рівня інфляції, нарахування податків,  підвищення і зниження цін на товар,  визначення рентабельності підприємств, тощо…

Пропонуємо вам задачі,  зв’язані з економічними розрахунками

Задача 1

У результаті інфляції у державі N ціни зросли на 300%. Визначте, на скільки відсотків потрібно знизити цін, щоб повернути їх до попереднього рівня.

Розв'язання

Нехай ціни у державі N були х одиниць, значить вони зросли на

одиниць і стали: () одиниць.

Знайдемо відсоткове відношення  чисел х і 4х, тобто

.

Тоді

Відповідь. На 75% потрібно знизити ціни.

Для  розминки вправа « Вірю не вірю»

Відповідають сигнальними картками так – червона, ні – зелена.

Кожна правильна відповідь 1 бал

1. Вклад збільшиться на 200%, якщо він потроїться?

                                                                  (так ).

2. Капітал збільшиться у 4 рази, якщо його збільшити на 300 %? (так).
3. Капітал зменшився у 4 рази ,то  він зменшився  на 75 відсотків? (ні)
4. На нараді акціонерів ВАТ “Білі береги” говорилося: “Дві третини інвестицій, що плануються, направлені у виробництво. Отже, на соціальну сферу залишається 30%”. Чи згоден ти з цим твердженням? (Ні).
5. Фірма “Веселка” платить рекламним агентам  5% від вартості замовлення. Треба  знайти замовлення на.40000грн  , щоб заробити 2тис грн.?(так )
6. У фірмі “Атланта” 60 співробітників. На прикінці місяця премію одержали 15% всіх співробітників. Це 19 чоловік одержали премію. (ні ).

 

Кулінарія

 

Задача 1

Житнє борошно дає 25% припічки. Скільки треба взяти борошна, щоб випекти 35 кг чорного хліба?

Розв'язання

Нехай, щоб випекти 35 кг чорного хліба потрібно взяти х кг житнього борошна. Тоді (кг) припічки. Маємо рівняння: звідки

Відповідь. Щоб випекти 35 кг чорного хліба, потрібно взяти 28 кг борошна.

Задача 2

Із свіжої малини виходить 15% сушеної . Скільки необхідно взяти свіжої малини, щоб отримати 6 кг сушеної?

Розв'язання

6 кг сушеної малини становлять 15%, отже знайдемо скільки кілограмів малини припадає на 1%  (кг), а вся свіжа малина – 100 %, тоді (кг)

Відповідь. 40 кг свіжої малини.

 

Сільське господарство

 

Задача 1

Від тривалого зберігання ячмінь втрачає за перший рік 3 % своєї маси, а за кожний наступний по 1 %. Скільки залишиться від 100 ц ячменю через 4 роки?

Розв'язання

(ц) – втрати ячменю за перший рік зберігання.

(ц) – маса ячменю після першого року зберігання.

Використаємо формулу складних відсотків.

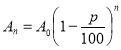
Оскільки ячмінь втрачає у масі, то у формулі знак «—». Де р = 1%, n=3, A₀=97 ц.

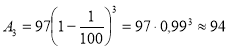
Отже, через 4 роки від 100 ц ячменю залишиться 94 ц.

Відповідь. 94 ц ячменю.

Задача 2

У першому бідоні є молоко, у якому масова частка жиру становить 2%, а в другому – молоко з масовою часткою жиру 5%. Скільки треба взяти молока з кожного бідона, щоб отримати 18 л молока, масова частка жиру в якому дорівнює 3%?

Розв'язання

Нехай з першого бідона взяли х л молока, а з другого – у л молока. В 18 л молока частка жиру дорівнює 3%, тобто (л) маємо рівняння

За умовою задачі отримаємо систему рівнянь:

Відповідь. 6 л і 12 л.

Підприємницька діяльність

 

Задача 1

Товар подешевшав на 25%. На скільки відсотків більше можна купити товару на ту саму суму грошей?

 

Розв'язання

Нехай товар коштував х грн., тоді після зниження ціни на 25 % став коштувати

грн. Тоді  

Відповідь. На більше можна купити товару.

 

Висновок

Знання про відсотки потрібні не лише математикам, оскільки відсотки мають тісний зв'язок з практичною діяльністю людини та з іншими науками.

Домашня робота

Розв’яжіть задачі.

1. В автопарку було 200 машин, 115 з яких – вантажівки. Скільки відсотків усіх машин автопарку є вантажівками? 2бали
2. Вкладник поклав до банку 10000 гривень під 14% річних. Скільки грошей буде на його рахунку через 2 роки? 4бали
3. Вартість деякого товару спочатку підвищили на 20%, а потім знизили на 20%. На скільки відсотків і як змінилась початкова ціна товару? 2бали
4. Скільки кілограмів 40% - го і скільки кілограмів 50% - го сплавів цинку треба взяти, щоб отримати 50кг 46% - го сплаву? 4бали

 

VІІ. Підсумок уроку. «Незакінчені речення»

1. «На сьогоднішньому уроці ми повторили…..»
2. «На сьогоднішньому уроці я зрозумів, що…..»
3. «На початку уроку я поставив перед собою мету. Ось як я її досягнув….»

У кожного на парті є листочки різного кольору, які відповідають вашим оцінкам. Прикріпіть їх на наше імпровізоване дерево знань. Якщо урок сподобався – вгорі, ні – внизу крони.

12-10 – зелений колір              6-4 – оранжевий колір

9-7 – жовтий колір                     3-1 червоний колір

         Використана література

1. Бабенко С. П. Алгебра. Розробки уроків. 9 клас. -  Харків: Ранок, 2009.
2. Гуськова Л.Г. Задачі та вправи з хімії. -  Москва : Вища школа, 1976.
3. Дзюбинська М.М. Зроби цікавим урок математики. -  Тернопіль : Мандрівець, 2009. – 88 с.
4. Картінська І. Й. Нестандартні уроки з математики. - Тернопіль, 2002.
5. Капіносов А. М. Тематичне оцінювання. Алгебра 9 клас.- Дніпропетровськ : Інновація, 2005. – 72 с.
6. Кравчук В. Алгебра: Підручник для 9 кл. / В. Кравчук, М. Підручна, Г.Янченко. – Тернопіль: Підручники і посібники, 2009. – 256 с.

 

7. Мерзляк А.Г. Збірник задач і контрольних робіт з алгебри для 9 кл. / А.Г.Мерзляк, В.Б.Полонський, Є.М.Рабінович, М.С.Якір. – Х.: Гімназія, 2009. – 128 с.
8.  Мерзляк А.Г. Математика : Підручник для 6 кл. / А.Г.Мерзляк, В.Б.Полонський, М.С.Якір. – Х. : Гімназія, 2006. – 304 с.

Відповіді до тестів.

1. в;    2. в;    3. г;  4. г;     5. б;    6.а;

  7. а;     8. б;    9.а; 10. г;    11. в;  12. г.

 

 

Тести	12б.
Задачі від банкірів	3б.
Задачі від хіміків	4б.
Вірю не вірю	6б.
Задачі на вибір	3б, 2б
домашня задача	6б.
Сума балів	34б.

 

 

Кількість набраних балів	Оцінка
34	12
33	11
32	10
31	9
30-28	8
27-25	7
26-24	6
23-19	5
18-16	4
15-12	3