Урок "Відстань між двома точками із заданими координатами" (з використанням методів розвитку критичного мислення)

                                                                          Урок  геометрії  (9клас)

Тема: Відстань між двома точками із заданими координатами

Геометрія: підруч. для 9 кл.  загальноосвіт.  навч.  закл. / О. С. Істер, -Київ: Генеза, 2017.

Навчальна складова мети уроку:  повторення основних понять декартової системи координат і координат точки на площині, дослідження можливості визначення відстані між двома точками через їх координати, виведення, обґрунтування відповідної формули та її застосування при розв′язуванні задач.

Розвивальна складова мети уроку: формування та вдосконалення навичок  критичного мислення; розвиток  пізнавальної, особистісної, самоосвітньої, соціальної, комунікативної компетенцій.

Виховна складова мети уроку: формування поведінкових компетенцій, навичок роботи в групі, парах; виховання активності, лаконічності, акуратності, толерантності.

Тип уроку: урок засвоєння нових знань.

Технічне обладнання та програмне забезпечення: презентація, індивідуальні картки, мультимедійна дошка, проектор.

 

Хід уроку

І. Психологічне  налаштування   учнів.

Учитель: Добрий день, друзі!  Я рада бачити вас усіх! У парах поверніться один до одного, з′єднайте долоні своїх рук, усміхніться  і обміняйтеся побажаннями: «Я щиро бажаю тобі ...».

ІІ.    Актуалізація  навчального досвіду учнів з теми, що вивчається.

ІІІ. Перевірка домашнього завдання.

Учитель: «Мало мати хороший розум, головне — правильно його використовувати» -  сказав великий  Рене Декарт. Сьогодні ми продовжуємо працювати з його безмежною системою координат.

Фронтальне опитування «Ромашка запитань»

    Задано точки А(-2;4),  С(0;2), В(-1;-7), М(-6;0), Д(4;-8),  К(2;5), Р(а;в),  Е(|с|+1; в),   L(m;3).

     Учні вибирають одну з пелюсток ромашки і формулюють для учнів класу запитання, використовуючи   задані точки.

      Наприклад.  «Чи належить точка С осі ОУ?», «Чому дорівнює відстань від точки В осі ОХ?», «При якій умові точка А є серединою відрізка КL?», « При якій умові точка Р належить бісектрисі другого координатного кута?». Учитель теж може поставити учням запитання. 

        Один учень у цей час працює біля дошки, відтворюючи хід розв»язання домашньої задачі .

Задача. За заданим малюнком знайти площу та периметр трикутника АВД, вважаючи, що кожна клітинка – квадрат зі стороною 1см.

Р о з в′ я з а н н я. У трикутнику АВД побудуємо висоту ВК. Тоді .

      Побудуємо на сторонах АВ та ВД як на гіпотенузах прямокутні трикутники з катетами 4см, 3см  та  4см, 4см.  Тоді за теоремою Піфагора:   АВ²=3²+4²=25,  ВД²=4²+4²=32.        Звідси    АВ=5см, ВД=

В і д п о в і д ь.

     Учень, який працював біля дошки, презентує розв′язок задачі. Після його відповіді з метою проміжного узагальнення  знань учнів з теми, що вивчається,  проектується складена на попередніх уроках концептуальна таблиця 1.

 

ПРЯМОКУТНА СИСТЕМА КООРДИНАТ
1.Означення	2 осі, ОХ ОУ, ОУ- вісь ординат, ОХ- вісь абсцис
2. Належність точок	A(0;у) належить осі ОУ A(х;0) належить осі ОХ
3.Відстань від точки до осей	А(х;у) до осі ОХ - |у|;   до осі ОУ - |х|;
4. Координати середини відрізка	, т.О-середина   АВ О (

ІV.  Мотивація навчальної діяльності.

V. Формулювання теми уроку.

Учитель: Пригадайте умову домашньої задачі №85(1). На яке запитання ви повинні були дати відповідь?

       Учні відповідають, що за заданими координатами чотирьох  точок вони встановлювали чи чотирикутник є паралелограмом.

Учитель: Пропоную вам додаткове запитання до  цієї задачі: А чи даний паралелограм АВСД є прямокутником? Що означає довести, що паралелограм - прямокутник?

       Учні вказують на необхідність виконання умови АС=ВД,  або ж і формулюють ознаку та означення прямокутника.

Учитель:  Чи можемо ми  знайти довжину діагоналей АС і ВД?

        Учні можуть дійти висновку, що не вміють у прямокутній системі координат знаходити відстань між двома точками.

Учитель: Сьогодні ми все ж таки дамо відповідь на поставлене мною запитання. Отже,  спробуйте сформулювати тему нашого уроку.

VІ. Вивчення нового матеріалу

Учитель: Чи знаходили ви відстань між двома точками без використання лінійки?

         Учні згадують формулу знаходження відстані на координатній прямій: відстань між двома точками на координатній прямій дорівнює модулю різниці їх координат.

Учитель: Оскільки осі Ох та Оу є координатними прямими, то це означає, що ми вміємо знаходити відстань АВ, якщо відрізок АВ лежить на одній із осей.

       Проектується таблиця 2.

Відстань між точками А і В	А(→   АВ=ǀ|=|
	А(→   АВ=ǀ|=|

 

Учитель: А чи можна знайти відстань між точками А і В за заданими їх координатами, якщо відрізок АВ паралельний одній із осей координат? 

        Учитель пропонує учням об′єднатися у пари та за готовими малюнками  знайти довжину відрізка АВ. 

    

 

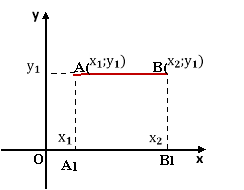
     Після обговорення отриманих результатів таблиця 2.  доповнюється новими записами.

                                                                                                          Таблиця 3.

Відстань між точками А і В	А(→    АВ=ǀ|
	А(→   АВ=ǀ|
	А(→    АВ=ǀ|
	А(→   АВ=ǀ|

 

Прийом  «Пазл». Кожному учневі пропонується на картці завдання на знаходження довжини відрізка (відрізок лежить на координатній осі або паралельний їй). Наприклад: «Знайти відстань між точками А(-2;4) і В(6;4)»,  «Знайти відстань між точками А(а;6+с) і В(а;с)» і т.д. Учні, які отримали однакові відповіді,  об′єднуються в одну групу. Формується чотири групи.

Робота у групах

Учитель: Як знайти відстань між точками А(, якщо відрізок АВ не лежить на координатних осях і непаралельний їм?

       Рене Декарт сказав: “Нащадки будуть вдячні  мені не тільки за те, що я сказав, але й за те, що не сказав, бо  цим самим дав їм можливість і задоволення здогадатися про це самостійно”. Тому  даю вам можливість самостійно у групах  опрацювати задачу 5(1) ст.23 підручника з відомими вам позначками («!», «?»,     «-«, «+») та заповнити схему виведення формули:

Прийоми «Інсерт» (читання з позначками) та «Кластер» (виділення змістових одиниць тексту).

      Після проведення підсумків роботи у групах та обговорення отриманих результатів пропонується узагальнений ланцюговий кластер:

 

 

Учитель: А чи справедлива дана формула для обчислення довжини відрізка, якщо він лежить на одній з осей координат або паралельний їй?

    Кожній групі пропонується розглянути один із чотирьох випадків таблиці 3.

    Учні роблять висновок, що виведена формула справедлива для будь-яких відрізків, незалежно від їх розташування.

      Повторно проектується концептуальна таблиця 1 з доповненим рядком:

 

5. Відстань між двома точками

АВ=

 

VІІ. Первинне закріплення вивченого матеріалу

Прийом «Вірю не вірю» з обгрунтуванням своєї відповіді

1. Якшо А(1;-2), В(6;5), то	3. Якшо А(-3;-2), К(1;-5), то
2. Якшо С(-1;-2), М(-4;5), то	4. Якшо Д(4;-12), В(0;5), то

 

Колективне розв′язання № 73  (один учень розв′язую біля дошки, решта – у зошитах).

№73(1)       ;

№73(2)      .

VІІІ. Формування нового навчального досвіду, умінь та навиків.

Учитель: Розв′яжемо задачу з домашньої роботи іншим способом, використавши навчальний матеріал сьогоднішнього уроку. Введемо прямокутну систему координат. Вважаючи, що одиничний відрзок – 1 клітинка, вкажіть, координати вершин трикутника та знайдіть його сторони й периметр.

               Учні записують: А(0;0),  В(3;4),  Д(7;0),     АД = 7

,            .

Учитель: Вважаючи, що довжина одиничного відрізка дорівнює 1см,  периметр даного трикутника дорівнюватиме  Такий метод розв′язання задач має назву «метод координат». Чи залежить, на вашу думку, відстань між двома точками від вибору системи координат?

                Учні висловлюють власні думки.                           

Кожній з груп пропонується за заданим малюнком знайти периметр трикутника АВД,  вважаючи, що одиничний відрізок  -1 клітинка.

              

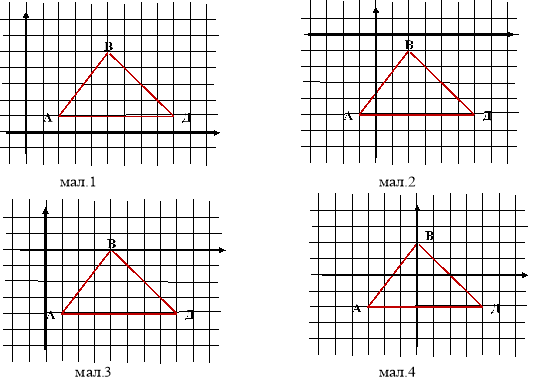
             З метою раціонального використання часу лідер групи повинен  розподілити ролі між учнями у процесі розв′язання задачі. Отримані результати вносяться у таблицю:

	І група мал. 1	ІІ група мал. 2	ІІІ група мал. 3	ІV група мал. 4
Координати вершин трикутника	А(… ;…) В(… ;…)  Д(… ;…)	А(… ;…) В(… ;…)  Д(… ;…)	А(… ;…) В(… ;…)  Д(… ;…)	А(… ;…) В(… ;…)  Д(… ;…)
Довжини сторін	АВ=	АВ=	АВ=	АВ=
	АД=	АД=	АД=	АД=
	ВД=	ВД=	ВД=	ВД=
Периметр трикутника

 

Учитель: Який висновок ви можете сформулювати?

         Учні формулюють висновок, що довжина відрізка не залежить від розміщення прямокутної системи координат.

Поєднання колективної й індивідуальної роботи учнів

Задача №90. Знайдіть довжину медіани АМ трикутника АВС, якщо  A(6; 0),  

                       В(–3; 4), С(7; 2).

Після обговорення шляхів розв»язання даної задачі 1 учень розв»язує її біля дошки, решта – у зошитах.

 

==5.

Відповідь. 5

       Двоє учнів  у цей час на бокових полях дошки за умовою цієї ж задачі обчислюють довжини медіан ВД та СК

.

Учитель: Знаючи координати точок М, К і Д, які елементи у цьому трикутнику ще можна знайти?

   Учні вказують, що можна знайти середні лінії.

Учитель: А чи можна встановити вид цього трикутника за сторонами?

  Учні роблять припущення, що оскільки АМ ≠ ВД ≠ СК, то трикутник  – різносторонній. 

Учитель: А як ще можна довести, що трикутник є різностороннім?

     Учні вказують, що потрібно знайти його сторони і порівняти.

Учитель: Нехай у прямокутній системі  знову задано три точки А, В, С з деякими координатами.  Як встановити чи трикутник АВС є рівнобедреним? прямокутним? 

           Учні зазвичай вказують тільки необхідні умови: рівність двох сторін, виконання співвідношення між сторонами трикутника: с²=а²+в², де с – найбільша сторона.

Учитель: Вірно, але це якщо в умові задачі сказано, що А, В, С -  вершини трикутника. А якщо ні?

           Учитель спонукає учнів дійти висновку, що потрібно перевірити виконання нерівності трикутника. 

Учитель: Пропоную вам розв′язати задачі такого типу.

       Учні у групах розв′язують задачі, знову ж розподіливши ролі між її членами:

І група - задача №79, ІІ і ІІІ група – задача №86 (вказати різні способи розв′язання),  група ІV – задача №100,

        Підводяться підсумки роботи у групах.

Задача №79.   А(–1; 2), B(0; 6), С(–5; 3) -вершини трикутника АВС. Доведіть,       

                        що трикутник АВС – рівнобедрений.

Р о з в′ я з а н н я.      ;

;.

    Оскільки АВ=АС, то за означенням рівнобедреного трикутника ∆АВС – рівнобедрений.

Задача №86. У трикутнику АВС   А(–4; 2), В(4; 7),  С(–2; 12). Знайдіть 

                     довжину  середню лінію, яка паралельна стороні АС.

Нехай КМ- середня лінія ∆АВС, КМ || АС.

  Тоді за означенням середньої лінії  ВК=КА, ВМ=МС.

     Отже,  .

Відповідь.

    Існує інший спосіб розв′язання задачі:

.

    Тоді за властивістю середньої лінії  КМ= .

    Якщо дві групи розв′язали задачу однаковим способом, то учитель пропонує  учням знайти й інший спосіб. Після цього учні вказують на раціональніший із них. 

Задача № 100.  Доведіть,  що  точки А(–1; –2),  В(3; 2) і  С(8; 7)  лежать  на   

                          одній прямій. Яка з точок лежить між двома іншими?

;
                                    ;

                                    .

      Оскільки АС = ВС + АВ, то точки А, В, С лежать на одній прямій і точка В лежить між точками А і С.

ІХ.  Підсумок уроку. Рефлексія.

Учитель: «Еврика» - крикнув Архімед, коли відкрив відомий вам закон. А що відкрили для себе ви на сьогоднішньому уроці?  Яким був ваш  емоційний стан під час уроку і яким він є зараз?

         Учні відповідають і повторно проектується доповнена концептуальна таблиця 1.

Учитель: Так чи є паралелограм АВСД у задачі №85(1)  прямокутником?

    Учні пропонують за вивченою на уроці формулою знайти його діагоналі.

    Учитель розподіляє завдання між учнями: дві групи знаходять діагональ  АС,  а дві інші – діагональ ВД.

        ;

       .

        Учні формулюють висновок, що оскільки АС≠ВД, то АВСД не є прямокутником.

Учитель: Задачі на встановлення виду чотитрикутника та знаходження його елементів, характеристик ми розглядатимемо на наступному уроці. А для цього необхідно повторити означення, ознаки відомих чотирикутників та закріпити вивчений матеріал на сьогодніщньому уроці під час виконання практичних задач.

        Учні записують домашнє завдання:

опрацювати теоретичний матеріал (ст.23 підручника), повторити навчальний матеріал за 8 клас ( означення, ознаки відомих чотирикутників), розв»язати задачі №70(1), 74, 80, 91, 101, 106 (з них 4 завдання на вибір).

Учитель: Дякую вам за те, що сьогодні зуміли «правильно використовувати» свій  розум, за те, що впродовж усього уроку ДУМАЛИ, навіть, і якщо помилялися. Бо як знову ж сказав Рене Декарт: «Я мислю — отже існую!».

        Підійдіть, будь-ласка,   до нашої символічної карти островів і зробіть свою позначку.

       Учні  чіпляють різнобарвні стікери біля одного з островів: «Радості», «Відкриття», «Інтересу», «Незадоволення», «Здивування», «Розчарувань».

 

                                                 Розробила: Жолобанюк О.Д., учитель математики

                                                 Борщівської загальноосвітньої школи І-ІІІ ст. №2

                                                Тернопільської області