Урок "Властивості арифметичного квадратного кореня"

Арифметика — це лічильна мудрість. Без цієї мудрості

 ні філософа, ні лікаря не може бути.

Л. П. Магницький

Тема уроку. Властивості арифметичного квадратного кореня.

Мета уроку.

Навчальна: формування вмінь  використовувати властивості арифметичного квадратного кореня при розв’язуванні завдань;

 Розвиваюча: інтелектуальний розвиток учнів, розвиток логічного мислення, пам’яті, уваги, інтуїції, уміння аналізувати, робити умовиводи за аналогією.

Виховна: виховання акуратності записів, чіткості й точності думки, працелюбства, наполегливості, алгоритмічної культури.

Тип уроку: УРОК ЗАСВОЄННЯ НОВИХ ЗНАНЬ
Методи і прийоми: математичний диктант, розгляд математичних софізмів, метод «Мікрофон».

Хід уроку

І.  Організація класу .

ІІ. Актуалізація і корекція опорних понять та уявлень.

Математичний диктант.

Учні записують тільки слова так , ні..

1. Числа -5 і 5 є квадратними коренями числа 25.(так)
2. Квадратний корінь з від’ємного числа є число від’ємне.(ні)
3. Квадратний корінь з числа а називають число квадрат якого дорівнює а.(так)
4. Квадратний корінь з числа -100 є число -10.(ні)
5. Арифметичний квадратний корінь з числа 0,64 є 0,08.(ні)
6. Арифметичний  квадратний корінь із числа 81 є числа 9 і -9(ні)
7. Арифметичним квадратним коренем з числа а називають від’ємне число, квадрат якого дорівнює а.(ні)
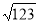8.  ()²= 123. (так)
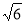9. (-)² =6. (так).
10. Вираз 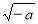має зміст лише при не додатних значеннях а (так)
11. Вираз 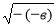має зміст лише при  не додатних значеннях в.(ні)
12. Вираз 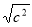має зміст при будь-яких значеннях с.(так)

Учні обмінюються зошитами і виконуємо разом оцінювання, даючи правильні відповіді на запитання. Аналізуються ті завдання де допущено найбільше помилок. Правильна відповідь +1 бал.

ІІІ. Повідомлення теми, мети і завдань уроку.

Отже, на попередніх уроках ми вивчили поняття квадратного кореня та арифметичного квадратного кореня, навчилися їх шукати. Та є ряд завдань, які виникають перед людьми, для розв’язання яких потрібно знати значно більше. Зокрема, властивості арифметичного квадратного кореня. Тож відкрийте зошити і запишіть тему уроку: «Властивості арифметичного квадратного кореня»

IV. Мотивація навчальної діяльності учнів.

Життя ставить перед нами щодня свої вимоги і  завдання. Досить часто потрібно розв’язувати завдання із використанням нових способів і  методів, які вчить нас математика. Бо саме ця наука найкраще вчить міркувати по новому, узагальнюючи й вдосконалюючи наші вміння. Логічні задачі із життя нерозривно зв’язані із завданнями математики. Є й досить багато підприємств, організацій, які для покращення умов людського існування відкривають нові можливості для людства, винаходять нові прилади і обладнання, винаходять нові технології для розвитку галузей медицини, освіти, промисловості, науки і техніки.. Ця робота зв’язана з великим об’ємом математичних обчислень де не обходиться без використання знаходжень арифметичних квадратних коренів.

А тепер уявіть ситуацію коли необхідно виконати наступні обчислення:

Для обчислень даних виразів необхідно скористатися властивостями які ми сьогодні будемо вивчати.
V. Сприймання нового матеріалу та його усвідомлення.

Отже, властивість 1. Для будь якого дійсного числа а виконується рівність .

Доведення випливає з рівності .

Які приклади , ми можемо розв’язати, використовуючи дані властивості?

Очікувана відповідь. Приклад 1, 5.

Учнів розв’язують, кажуть результати вчителю. Для слабших учнів робляться записи на дошці.

Властивість 2.Для будь якого дійсного числа а і натурального числа п виконується рівність

.

Використовуючи дану властивість ми з вами зможемо виконати приклади 4 і 8.(вчитель виконує на дошці з поясненням кожного кроку).

Властивість 3.Для будь-яких дійсних чисел а і b  таких, що а, виконується рівність

.

Розгляньте приклади9, 2 і 6.

В прикладі 9 обчислюємо окремо корінь із 100 та корінь із 3600 і шукаємо добуток результатів..

Використовуючи дану властивість ми можемо внести числа під один корінь в прикладі 2. Отримаємо  арифметичний корінь із 36 рівний 6. А в прикладі 6, внісши все під знак кореня,  число 34 запишемо як два множники 17 і 2.Отримаємо

Властивість 4 Для будь-яких дійсних чисел а і b  таких, що а, виконується рівність

Використовуючи дану властивість виконайте самостійно приклади10, 3 і 7.
VI. Узагальнення та систематизація набутих знань.

1)Усно №471, №479,№485.

2)Розглянемо математичний софізм:

1.Знайдіть де допущена помилка в моїх міркуваннях.

Я стверджую, що 4=5, бо   16-36=25-45,   16-36+20= 25-45+20,      (4-=    (5-, 4-, 4=5.

3)Письмово №473(непарні), №478(непарні),№482, №487.

VII. Підсумки уроку.

Метод «Мікрофон»

Дайте відповіді на запитання:

1. Що таке арифметичний квадратний корінь?

2. Чи існує арифметичний корінь з будь-якого числа?

3. Сформулюйте властивості арифметичного квадратного кореня?

4. Чи важливим є використання даних властивостей при виконанні обчислень?

5.Наведіть приклади 

VIII. Домашнє завдання.
Вивчити п 15 (теореми та доведення), запитання 1-5 (ст.118).

№472,№476,№480(усно)