Урок з алгебри в 8 класі з теми «Розв’язування вправ на застосування властивостей степеня з цілим показником»
Тема «Розв'язування вправ на застосування властивостей степеня з цілим показником»
Мета:
1) навчальна:узагальнити знання учнів з даної теми; повторити означення степеня з цілим показником та стандартного вигляду числа; навчити застосовувати властивості степеня з цілим показником до розв'язування вправ; повторити відомості про обернену пропорційність як функцію,побудову її графіка, дослідження властивостей оберненої пропорційності;
2) розвиваюча: сприяти формуванню та розвитку в учнів інтелектуальних і творчих здібностей, увагу, пам'ять, вміння слухати товариша; розвивати математичну мову у процесі повторення та узагальнення матеріалу теми та при перетворенні виразів і знаходженні числового значення; вдосконалювати обчислювальні навички школярів, достатні для вільного їх використання у вивченні математики і суміжних предметів, а також у процесі розгляду різноманітних практичних застосувань математичних знань;
3) виховна: виховувати інтерес до математики, старанність i працьовитість.
Тип уроку:формування вмінь та навичок.
Наочність та обладнання: конспект уроку, ноутбук, проектор, дидактичний матеріал, підручник.
Урок № 27 Алгебра, 8-А клас
Тема «Розв’язування вправ на застосування властивостей степеня з цілим показником»
Мета:
- навчальна:узагальнити знання учнів з даної теми; повторити означення степеня з цілим показником та стандартного вигляду числа; навчити застосовувати властивості степеня з цілим показником до розв’язування вправ; повторити відомості про обернену пропорційність як функцію,побудову її графіка, дослідження властивостей оберненої пропорційності;
- розвиваюча: сприяти формуванню та розвитку в учнів інтелектуальних і творчих здібностей, увагу, пам'ять, вміння слухати товариша; розвивати математичну мову у процесі повторення та узагальнення матеріалу теми та при перетворенні виразів і знаходженні числового значення; вдосконалювати обчислювальні навички школярів, достатні для вільного їх використання у вивченні математики і суміжних предметів, а також у процесі розгляду різноманітних практичних застосувань математичних знань;
- виховна: виховувати інтерес до математики, старанність i працьовитість.
Тип уроку:формування вмінь та навичок.
Наочність та обладнання: конспект уроку, ноутбук, проектор, дидактичний матеріал, підручник.
Хід уроку
- Організаційний етап. Оголошення теми та мети уроку.(1хв.)
Доброго дня, я рада вас бачити! Я хочу почати урок з таких слів
«Нехай хто-небудь спробує викреслити з математики степеня, і він побачить, що без них далеко не заїдеш». (М. В. Ломоносов)
Ці слова ми візьмемо за девіз нашого уроку, на якому ми будемо узагальнювати та закріплювати знання з теми «Функція у = ![]() , де к ≠ 0» та «Степінь з цілим показником», покажемо зв'язок даної теми з іншими науками та сферами діяльності. І головне завдання нашого уроку – закріпити вміння перетворювати та обчислювати вирази, що містять степені з цілим показником, щоб добре підготуватися до контрольної роботи.
, де к ≠ 0» та «Степінь з цілим показником», покажемо зв'язок даної теми з іншими науками та сферами діяльності. І головне завдання нашого уроку – закріпити вміння перетворювати та обчислювати вирази, що містять степені з цілим показником, щоб добре підготуватися до контрольної роботи.
- Перевірка домашнього завдання. (5 хв.)
1. Обчисліть значення виразу: а) (-2)-3 ∙ (-5)0; б) 3-5 : (3-6 : 3-2).
2. Спростіть вираз: а) (6а-2b-3)2; б) (2a )-2 ∙ 8 a 3.
3. Побудуйте графік функції ![]() . Користуючись побудованим графіком, знайдіть корені рівняння
. Користуючись побудованим графіком, знайдіть корені рівняння ![]() = х + 2;
= х + 2;
- Актуалізація опорних знань та вмінь. (15 хв.)
- Вправа « Асоціативний кущ»
Питання до класу: Які поняття у вас асоціюються з функцією « Обернена пропорційність»?
А зараз прослухаємо звіт творчої групи учнів про виконану пошукову роботу на тему «Застосування графіка оберненої пропорційності і інших сферах діяльності»
Розглянемо прояви оберненої пропорційності у явищах природи та галузях людської діяльності. Цим ми ще раз підтвердимо слова Г. Галілея: «Природа формулює свої закони мовою математики».
- Обернена пропорційність у біології:
У біології можна знайти багато прикладів обернено пропорційних залежностей: Наприклад, чисельність особин певного виду на деякій території i кількість корму, розміри тварин та їхня рухливість (наприклад, порівняємо ящірку i варана, слона та мишку); діаметр кровоносних судин і тиск крові (із звуженням судин тиск крові збільшується).
2. Обернена пропорційність у фізиці:
1) Залежність тиску від площі поверхні
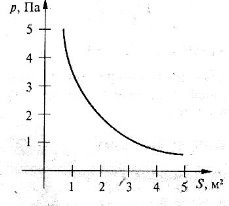 Ця залежність описується графіком p =
Ця залежність описується графіком p = ![]()
Тиск, який чинить тіло на деяку поверхню, обернено пропорційний до площі цієї поверхні.
За графіком бачимо, що із збільшенням площі поверхнізменшується тиск на неї, i навпаки.
Наприклад, людині важко йти по пухкому снігу, вона провалюється на кожному кроці. Але на лижах можна йти по снігу, майже не провалюючись у нього. Сила, з якою людина діє на сніг, в обох випадках однакова, проте різна площа поверхні на яку тисне людина на лижах i без них.
3) Залежність між швидкістю і часом
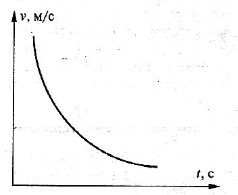
Певну відстань із більшою швидкістю можна проїхати за менший час, за умови зменшення швидкості їхати доведеться довше. Отже, швидкість i час обернено пропорційні величини.
3.Обернена пропорційність в економіці
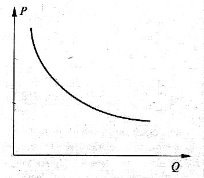
В економіці прикладом оберненої пропорційності є закон попиту: якщо ціна якогось товару підвищується i при цьому решта умов залишається незмінними, попитом буде користуватися менша кількість цього товару.
- Інтерактивна вправа «Математичний переполох»
-

-
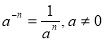
-
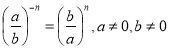
-
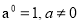
-
am
 an=am+n
an=am+n
- am:an=am-n
- (am)n=amn
- b = a·10n, 1≤ a <10
- (ab)n=anbn
-
(
 )n=
)n=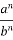 .
.
- Інтерактивна вправа « Знайди помилку»
-
a-6
 a9=a-6+9=a-3
a9=a-6+9=a-3
- a7:a-3=a7+(-3)=a4
-
(2a4
 b-2)-3=2a-12
b-2)-3=2a-12 b6
b6
-
95
 9-7=97-5=92=81
9-7=97-5=92=81
-
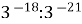 =
=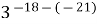 =3-39
=3-39
-
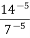 =(
=(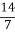 )-5=2-5 =
)-5=2-5 = 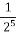 =
= 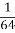 .
.
-
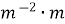 =
=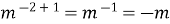
-
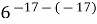 =
= 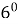 =0
=0
- 35400=3,54∙105
- 0,00248=24,8∙10-3
- Формування вмінь і навичок (20 хв.)
- Робота з підручником № 293 с. 66 (Мерзляк А.Г., Полонський В.Б., Якір М.С.)
Знову звертаємось за допомогою до творчої групи. Учасники творчої групи також з’ясовували, які науки крім математики працюють з числами, записаними в стандартному вигляді.
- Робота в парах
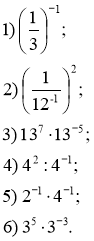
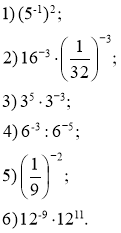

3. *Додатково. Знайдіть значення виразу:
1) ![]() ; (
; (![]() =8=
=8=![]() =, 2-9
=, 2-9![]() =
= ![]() )
)
2) ![]() ; (
; (![]() =
=![]() , 9=
, 9=![]() .
. ![]() =
=![]() :
:![]() =
=![]() =
=![]() =
=![]() =9)
=9)
3) 100-2 :1000-5![]() 0,016; (100-2 :1000-5
0,016; (100-2 :1000-5![]() 0,016=(102)-2 :
0,016=(102)-2 :![]() =
= ![]() =
=![]() =
=![]() =
=![]() =0,1
=0,1
VI. Підсумки уроку. Виставлення оцінок (3 хв.)
Демонстрація кластера « Степінь з цілим показником»

VII. Домашнє завдання. (1 хв.)
Повторити п.8-10, № 281, 294, 338*
Робота в парах
I ряд II ряд III ряд
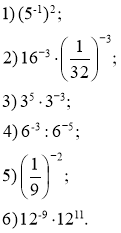

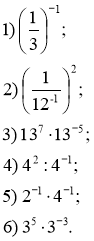
|
1 ряд |
|||||
|
0,04 |
0,125 |
9 |
125 |
81 |
144 |
|
2 ряд |
|||||
|
0,25 |
25 |
144 |
9 |
27 |
144 |
|
3 ряд |
|||||
|
3 |
144 |
169 |
64 |
0,125 |
9 |
3. *Додатково. Знайдіть значення виразу:
1) ![]() ; 2)
; 2) ![]() ; 3) 100-2 :1000-5
; 3) 100-2 :1000-5![]() 0,016;
0,016;


про публікацію авторської розробки
Додати розробку
