Лінійні та квадратні рівняння з параметрами.Навчальний посібник

 

 

 

 

 

 

 

 

 

 

 

(Навчальний посібник)

 

 

                                                                                    

                  

                                                                                    

Рекомендовано до використання в освітньому процесі на засіданні методичного об’єднання вчителів математики, фізики та інформатики (Протокол №3 від 14.01.2020)

 

 

Автор: Олійник В.О. – вчитель математики Полонської загальноосвітньої школи І-ІІІ ступенів №3

 

 

Рецензент:

• Грицак О.Є. – голова методичного об’єднання вчителів математики, фізики та інформатики Полонської загальноосвітньої школи  І-ІІІ ст.№3

 

 

 

 

 

 

 

 

 

 

В роботі дано визначення рівняння з параметрами. Висвітлено алгоритм розв’язування лінійних та квадратних рівнянь з параметрами. Розглянуто різні випадки розміщення коренів в квадратному рівнянні з параметрами. Описано на прикладах графічний спосіб розв’язування рівнянь, що містить параметр.

Такі задачі найбільш відображають рівень математичного та логічного мислення, формують початкові навички дослідницької діяльності та математичну культуру.

Ця тема досить актуальна, тому що задачі такого типу зустрічаються в завданнях високого рівня на уроках алгебри, олімпіадних завданнях з математики, у завданнях для державної підсумкової атестації та ЗНО з математики.

Матеріали даної роботи можуть бути використані на уроках математики, у проведені спецкурсів, факультативів, у написанні курсових та дипломних робіт з математики.

ЗМІСТ
Вступ	4
РОЗДІЛ 1. Найпростіші рівняння з параметрами	5
1.1. Означення рівняння з параметрами	5
1.2. Лінійні рівняння з параметрами	6
РОЗДІЛ 2. Квадратні рівняння з параметрами	8
2.1. Алгоритм розв’язування квадратних рівнянь з                        параметрами	8
2.2. Дослідження значення коренів квадратного рівняння	9
2.3. Співвідношення між коренями квадратного тричлена	12
2.4. Розміщення коренів квадратного тричлена відносно                        чисел	13
2.5. Розміщення коренів квадратного тричлена відносно                        інтервала	16
РОЗДІЛ 3. Графічне розв’язування рівнянь з параметрами	20
Висновки	23
Використана література	24

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ВСТУП

Однією із складних тем шкільного курсу  математики є розв’язування задач з параметрами. Потрібно вміти не тільки вміти розв’язувати рівняння за певним алгоритмом, але й вміти дослідити їхні розв’язки. Саме   розв’язування задач з параметрами значною мірою розвиває абстрактне мислення , спонукає до пошукової діяльності, формує навички аналізу – важливі для математичного розвитку особистості, якості, що застосовуються під час розв’язування задач з фізики, інформатики, економіки тощо.

Шкільною програмою не передбачено достатньо часу для набуття навичок розв’язування таких задач.

Саме такі задачі найбільш відображають рівень математичного та логічного мислення, формують початкові навички дослідницької діяльності та математичну культуру.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

РОЗДІЛ 1

Найпростіші рівняння з параметрами

 

1.        Означення рівняння з параметрами

 

          Для розв’язування задач у техніці і математиці досить часто доводиться    складати і розв’язувати рівняння. При цьому, нерідко, в ці рівняння, крім невідомих величин, входять також деякі інші змінні величини, що мають назву параметри.

          Параметр як фіксоване, але невідоме число, має ніби двоїсту природу. По-перше, передбачувана визначеність дає можливість «спілкуватися» з параметром як з числом, а по-друге – ступінь свободи спілкування обмежується його невизначеністю.

          Так, ділення на вираз, що містить параметр, добування коренів парного степеня з подібних виразів вимагають попередніх досліджень. Як правило, результати цих досліджень впливають і на їх розв’язування, і на відповідь.

Рівнянням з параметрами  називаємо рівняння виду ( х, а₁ , а₂ , … а_n ) = =0 , де х – шукане невідоме , а₁ , а₂ , … а_n – змінні параметри.

Значення шуканого невідомого х залежить від значення параметрів.

Значення параметрів а₁ , а₂ , … а_n при яких вираз ( х, а₁ , а₂ , … а_n ) має зміст при деяких значеннях х, називаються допустимими. Множину всіх допустимих систем значень параметрів рівняння ( х, а₁ , а₂ , … а_n ) = 0 називають областю змінних параметрів цього рівняння.

Для кожної допустимої системи значень параметрів рівняння                            ( х, а₁ , а₂ , … а_n ) = 0 має  певну множину розв’язків. Розв’язати рівняння з параметрами означає знайти всі розв’язки цього рівняння для кожної допустимої системи значень параметрів.

Щоб розв’язати рівняння  ( х, а₁ , а₂ , … а_n ) = 0 з невідомим х і параметрами  а₁ , а₂ , … а_n , треба:

1.               визначити область допустимих значень систем параметрів а₁ , а₂ , … а_n ;
2.               розв’язати рівняння відносно х і подати невідоме х у вигляді функції  

 х = g (, а₁ , а₂ , … а_n ) від параметрів;

3.               з’ясувати, при яких допустимих системах значень параметрів значення функції  х = g (, а₁ , а₂ , … а_n ) є розв’язками даного рівняння;
4.               розглянути рівняння  ( х, а₁ , а₂ , … а_n ) = 0, при таких допустимих системах значень параметрів, при яких його не можна розв’язати відносно х; з’ясувати, чи має рівняння при цих значеннях  параметрів розв’язки,  якщо має, то які.

 

2.        Лінійні рівняння з параметрами

 

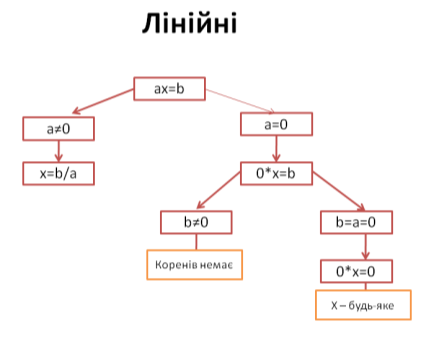
Рівняння виду ax+b=0, де х – невідоме, a,b – параметри називають лінійним рівнянням з параметрами.

Дослідимо його:

якщо a ≠ 0, то рівняння має єдиний розв’язок: х=- ;

якщо a = 0, b=0, то рівняння має вигляд: 0 × х = 0, звідки  х – будь-яке число;

якщо a = 0, b≠0, то рівняння має вигляд: 0 × х = - b, що неможливо. Рівняння не має розв’язків.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Приклад 1. Розв’язати рівняння а²х=а(х+2)-2.

Розв’язання:

               а²х=а(х+2)-2;    а²х=ах+2а -2   а²х-ах=2а -2; ах(а-1)=2(а-1);

а) якщо а=1, то маємо 0 × х = 0, х – будь-яке число;

б) якщо а≠1, то маємо х= :

в) якщо а=0,то  маємо    0 × х=2,    рівняння коренів немає;

г) якщо а≠0, то х =.

Відповідь: якщо а=1, х – будь-яке число;

  якщо а≠1 і  а≠0, то маємо х=;

          якщо а=0, то рівняння коренів немає.

 

Приклад 2. Знайти всі цілі корені рівняння ах = а + 5х, які кратні 3       

(а – будь-яке ціле число, що не дорівнює 5).

Розв’язання:

х (а – 5) = а

 Оскільки а ≠ 5 , то х = . За умовою  корені повинні бути кратні 3 , тобто =3k,  а = 3k (а – 5),  a= ,  де k є Z.

 Відповідь: х = для a=

  

Приклад 3. Визначити , для яких значень параметра а рівняння ( х-1)(а-2)=1 матиме розв’язок, що належить інтервалу (1;2)

Розв’язання:

Для а ≠ 2 маємо х – 1 = ;   х = 1 + ;    х = .

За умовою 1 < < 2 , тому перейдемо до системи:

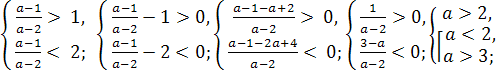  a >3.

Відповідь: х = для a >3.

 

Приклад  4. Розв’язати рівняння .                                                   

         Розв’язання:

Допустимі значення параметрів а≠0,  b≠0 , тоді x(a+b)=abc.

1. Якщо a = - b, с=0, то маємо рівняння : 0×x =0, x – будь-яке число.
2. Якщо a = - b, с≠0, то дістанемо рівняння : 0×x= -а²с, яке немає коренів.
3. Якщо a ≠ - b, то .

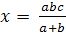Відповідь: якщо a = - b, с=0, то x – будь-яке число;

             якщо a = - b, с≠0, то немає коренів;

             якщо a ≠ - b, то .

 

 

 

 

 

РОЗДІЛ 2

Квадратні рівняння з параметрами

 

1.        Алгоритм розв’язування квадратних рівнянь з параметрами

 

 Рівняння виду ax²+bx+c=0, де х – шукане невідоме,  a, b, c, - параметри, a≠0, називається квадратним рівнянням з параметрами. Якщо a = 0, то рівняння перетворюється на лінійне і набирає вигляду: bx+c=0. Якщо a≠0,  то для рівняння ax²+bx+c=0   має D=b² – 4ac. Якщо

1. D>0, то рівняння має 2 дійсних корені:;
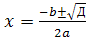2. D=0, то рівняння має один єдиний корінь: ;
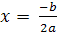3. D<0, то рівняння немає дійсних коренів.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Приклад 1. Розв’язати рівняння: 3( 2а – 1) x²-2(а + 1) x + 1= 0.

Розв’язання:

1. Якщо а= , то маємо: -2(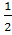 + 1) x+1=0;  -3x+1=0;  .
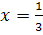2. Якщо а≠, то дане рівняння є квадратним. Знайдемо дискримінант :

D = 4(а + 1)² - 12(2а – 1) = 4(а² - 4а + 4) = 4(а - 2)² ,  D ≥ 0.

1. D>0, а≠2, то маємо корені: 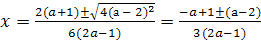,  звідси  x₁=,  x₂=.
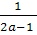2. D=0 , а=2, дане рівняння набуває вигляду:

9х²-6х+1=0;  (3х - 1)² =0;  .

Відповідь: якщо а= ,  а=2 , то ;

                  якщо  а≠, а≠2 , то  x₁=,  x₂=.

 

Приклад 2. Розв’язати рівняння: ( а ² + а – 2) x² + 2(а ²- 1) x + а ²= 0.

 

Розв’язання:

1. Якщо а ² + а – 2= 0, то а = 1 та а = -2

               а) а = -2, то маємо рівняння 6х + 4 = 0;  х = -

               б) а = 1, то 0 • х + 1 = 0, 0 • х = - 1

Рівняння не має розв’язків.

2. Якщо а ² + а – 2 ≠ 0, тобто а ≠ 1, а ≠ - 2, то знайдемо дискримінант рівняння:

= (а ²- 1) - а ²(а ²+а-2)= а ⁴- 2 а ²+1- а ⁴- а ³+2 а ²=1- а ³

а) D>0,  1- а ³>0, а ³<1, а<1, то рівняння має два розв’язки:

 

 

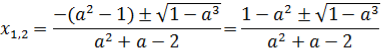
б) D=0,  1- а ³=0, а ³=1, а=1, то рівняння маємо таке рівняння:

    0•х²+0•х+ а ²=0, де х є Ø.

в ) D<0,  1- а ³<0,  а>1, то рівняння не має розв’язків.

Відповідь: якщо а≥1,  то розв’язків немає;

         якщо а=-2, то х=-

                

        якщо а<1, а ≠-2, то .

    

 2.2. Дослідження значення коренів квадратного рівняння

При розв’язуванні квадратних рівнянь з параметром, в яких потрібно дослідити значення коренів, необхідно знати такі теореми:

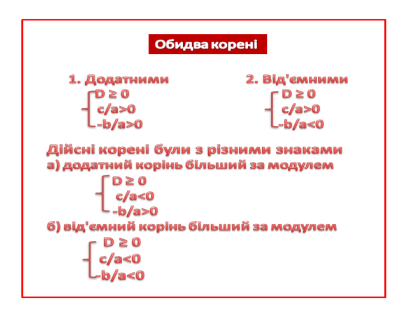
Теорема 1. Для того, щоб корені квадратного тричлена були дійсними і мали однакові знаки, необхідно і достатньо виконання таких умов:
 

 

 

 

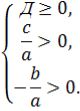При цьому обидва корені будуть додатними, якщо додатково виконується умова

х₁+х₂=->0, тобто
 

 

 

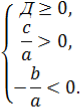Обидва корені будуть від’ємними, якщо х₁+х₂=-<0, тобто
 

 

 

 

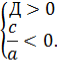Теорема 2. Для того, щоб корені квадратного тричлена були дійсними і мали різні знаки, необхідно і достатньо виконання таких умов:
 

 

 

При цьому додатний корінь більший за модулем, якщо х₁+х₂=->0, тобто

 

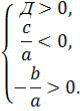
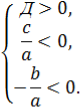
  Від’ємний корінь більший за модулем, якщо
 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Приклад 1. Знайти всі значення а, для яких корені рівняння

                      (а – 1)х²+2ах+а+3=0 додатні.

                                       Розв’язання.

1. Для а=1 умова задачі не виконується, бо 2х=-4; х=-2.
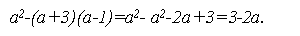2. Для а≠1. Обчислимо дискримінант:

 

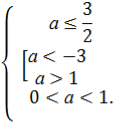
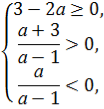Для того, щоб рівняння мало додатні корені, мають виконуватися умови:

 

 

 

 

Система несумісна, отже ні для яких значень а корені додатними не будуть.

Відповідь: Додатних значень а не має.

 

Приклад 2. Для яких значень а рівняння (а+5)х²+(2а-3)х+а-10=0

           має два від’ємні корені?

                                          Розв’язання

З умови задачі випливає, що а≠-5. Знайдемо дискримінант.

Д=(2а-3)²-4(а+5)(а-10)=4а²-12а+9-4(а²-5а-50)=4а²-12а+9-4а²+20а+200=8а+209.

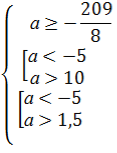
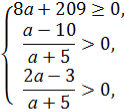
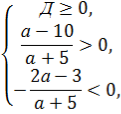Для того, щоб рівняння мало від’ємні корені, необхідно, щоб виконувалися умови:

 

 

 

 

 

 

                     

Отже, а є [                         - 5) U (10; + ∞)

 

Відповідь: а є [                   - 5) U (10; + ∞)

 

 

 

 

\

2.3. Співвідношення між коренями квадратного рівняння з параметрами

 

 Завдання на співвідношення між коренями квадратного рівняння з параметрами зручно розв’язувати не виписуючи значення коренів через дискримінант, а використовуючи обернену теорему Вієта, яка «працює» лише у випадку, коли корені квадратного рівняння дійсно існують, тобто коли дискримінант невід’ємний.

Якщо Д>0, то за теоремою Вієта:

 

 

При необхідності можна скористатись співвідношенням

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 Приклад 1. Не розв’язуючи рівняння х²- (2а +1)х+а²+2=0 , знайти для якого значення а один з його коренів у 2 рази більший за другий.

Розв’язання:

Знайдемо дискримінант: D=(2а +1)² - 4 а² – 8= 4а² + 4а +1 - 4 а² – 8= 4а -7.

Рівняння матиме два корені, якщо D>0, тобто 4а -7>0 , а > .

За умовою х₁ = 2 х₂ . За теоремою, оберненою до теореми Вієта, маємо: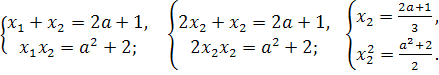

Отже,   ;

 8 + 8а+2-9-18 =0 ;   - 8а+16 = 0 ;    (а-4)²=0 ;   а=4.

Відповідь : а=4.

 

Приклад 2. При якому значенні параметра m сума квадратів коренів рівняння    х ²+ (2 - m)х – m-3 =0 найменша?

Розв’язання:

При умові D=(2 - m)²+4(m+3)≥0 маємо:

Тоді х₁²+ х₂²= ()²-2= (m-2)²+2(m+3)= m² - 4m + 4 + 2m + 6 =             = m² - 2m+10= (m-1)²+9  , приймає найменше значення при m = 1.

При m = 1 корені існують , бо D=(2-1)² + 4(1+3)= 17 >0.

Відповідь: m = 1.

 

Приклад 3 Знайти таке значення с, для якого корені рівняння                  х ²- 2+с=0 задовільняють умову

Розв’язання:

Знайдемо дискримінант: D=4-4с.

Рівняння має 2 корені , якщо D>0;   4-4с>0, тобто с<1.

За теоремою, оберненою до теореми Вієта:

За умовою задачі корені рівняння повинні задовольняти умову                   ;    7() -4=47;   -11=33; =-3.

Тоді =2-(-3)=5 , а підставивши значення у друге рівняння системи, одержимо: с=(-3)×5= -15.

Відповідь: с = -15.

 

2.4. Розміщення коренів квадратного тричлена відносно числа

 

Теорема 1. Для того, щоб обидва корені квадратного тричлена були менші за число М (М є R) ( тобто лежали на числовій прямій лівіше , ніж М ) необхідно і достатньо виконання таких умов:

для а>0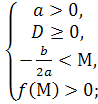  ,      а для а0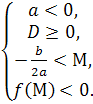

які можна записати у вигляді однієї системи: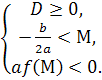

 

 

 

 

 

 

 

 

 

 

 

 

 

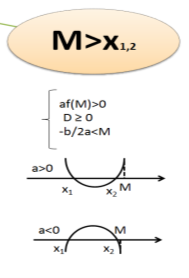
Теорема 2. Для того, щоб обидва корені квадратного тричлена були більшими за число М ( тобто лежали правіше, ніж М ), необхідно і достатньо виконання таких умов:

 для а>0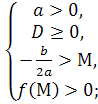        а для а0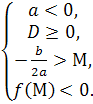

які можна записати у вигляді однієї системи: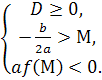

 

 

 

 

 

 

 

 

 

 

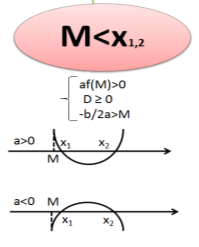
Теорема 3. Для того, щоб один з коренів квадратного тричлена був менший за число М, а другий більший за М ( тобто М лежить між коренями) , необхідно і достатньо виконання таких двох умов:

для а>0 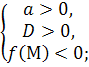   а для а0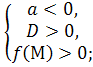

які виконуються також і тоді , коли .

 

 

 

 

 

 

 

 

 

 

 

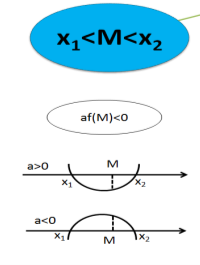
Приклад 1. При яких значеннях один з коренів рівняння             (а²+а+1)х²+(2а-3)х-а²-5=0 менший за 1 , а другий більший за 1 ?

Розв’язання:

За умовою задачі 1 лежить між коренями рівняння, тому виконується така умова:  (а²+а+1) f (1)<0, оскільки а²+а+1>0 при a є R, то а²+а+1+2а-3- а²-5<0,   3а-7<0,  а < .

Відповідь: при а є ( -∞; 2 ).

 

Приклад 2. Для яких значень k корені рівняння х² +(2k – 4)x+2k – 1=0, більші за 1.

Розв’язання:

Більший коефіцієнт рівняння додатний. Тому для того, щоб корені рівняння були більші за 1, треба , щоб виконувалися умови:

 

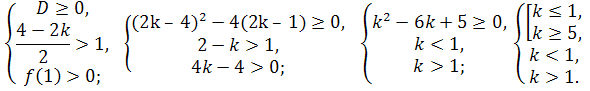
Система несумісна, тому значень при яких корені рівняння були більші за 1 не існує.

Відповідь: таких значень немає.

 

2.5.  Розміщення коренів квадратного тричлена відносно інтервалу

 

Теорема 1. Для того , щоб обидва корені квадратного тричлена були більшими за число М, але меншими , ніж число N  (M<N) ( тобто лежали між числа М і N, необхідно  і достатньо виконання таких умов:

 для а>0 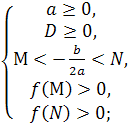,       а для а0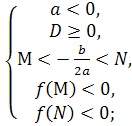

які можна записати також у вигляді однієї системи :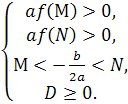

 

 

 

 

 

 

 

 

 

 

 

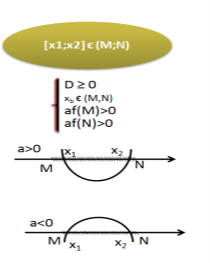
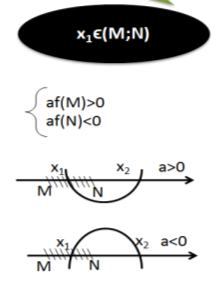
Теорема 2. Для того , щоб тільки більший корінь квадратного тричлена лежав між числами М і N (M<N) , необхідно і достатньо виконання таких двох умов:

для а>0 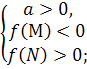,       а для а0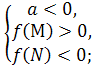

які можна записати також у вигляді однієї системи:

 

 

 

 

 

 

 

 

 

 

 

 

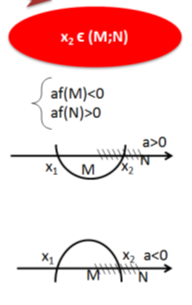
Теорема 3. Для того, щоб тільки менший корінь квадратного тричлена лежав між М і N (M<N), необхідно і достатньо виконання таких двох умов:

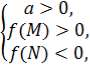              для а>0                                                            для а<0
 

 

які можна записати також у вигляді однієї системи:

 

 

 

 

 

 

 

 

 

 

 

 

 

Теорема 4. Для того , щоб один з коренів квадратного тричлена був менший за М , а другий більший за (M<N) ( тобто відрізок MN повністю знаходився між коренями), необхідно і достатньо виконання таких двох умов:

для а>0 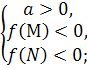       а для а0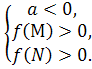

які можна записати також у вигляді однієї системи:

 

 

 

 

 

 

 

 

 

 

 

 

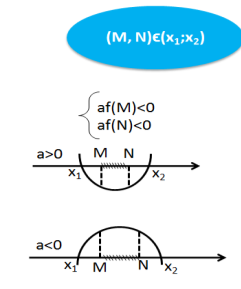
Теорема 5. Між двома коренями одного тричлена f(x) знаходиться тільки один корінь другого тричлена g(x) тоді і тільки тоді, коли g(x₁)• g(x₂)<0, де x₁ і x₂ корені f(x).

 

Приклад 1. При яких а корені рівняння 2х²-(2а – 5)х + а – 3 = 0 розташовані між числами 0 і 1 ?

Розв’язання:

 f(x) = 2x² – (2a-5)x + a -3.

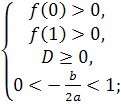
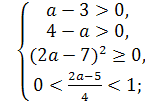
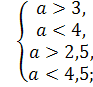                 a є ( 3; 4 ).

Відповідь: a є ( 3; 4 ).

 

Приклад 2. При яких значеннях а один із коренів квадратного рівняння

Розв’язання:

    f(x) = ax² – (3a-2)x + a -2. За умовою задачі a ≠ 0. Тоді маємо:

      ;         a є ( 0; ).

  Відповідь: a є ( 0; ).

 

Приклад 3. При яких значеннях a корені і рівняння

задовольняють умову  ?

         Розв’язання:

Нехай   f(x) = . Оскільки то вітки параболи   f(x) напрямлені вгору. Складемо і розв’яжемо таку систему нерівностей:

     

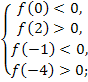
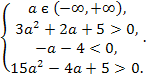
Відповідь: a >-4

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

РОЗДІЛ 3

Графічне розв’язування рівнянь з параметрами

 

Із шкільного курсу математики, нам відомо, що графічний спосіб, зазвичай, не дає можливість точно знайти корені рівнянь, але за допомогою графічної інтерпретації можна визначити найраціональніший спосіб знаходження кількості коренів рівнянь.

Поєднання графічного та аналітичного способів дасть змогу отримати правильний результат.

Розв’язувати рівняння з параметрами графічним способом зручно за таким алгоритмом:

1. знаходимо область допустимих значень рівняння.
2. виражаємо а як функцію від х.
3. у прямокутній системі координат будуємо графік функції a=f(x) для тих значень х, які входять в область допустимих значень даного рівняння.
4. Знаходимо точки перетину прямої а=с, де с є (-∞;+∞) з графіком функції a=f(x). Якщо пряма а=с перетинає графік a=f(x), то знаходимо абсциси точок перетину. Для цього досить розв’язати рівняння a=f(x) відносно х.
5. Записуємо відповідь.

 

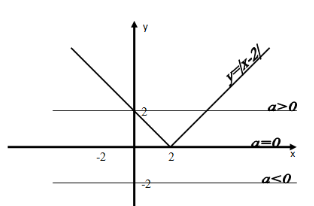Приклад 1. Скільки коренів має рівняння |x-2|=a залежно від параметра?

 

В системі координат (х; у) будуємо графік функцій у=|x-2| та у=a.

З побудови бачимо:

1. Якщо a<0, то розв’язків немає.
2. Якщо a=0, то 1 розв’язок х=2.
3. Якщо a>0, то 2 розв’язки.

 

 

 

Приклад 2. Скільки коренів має рівняння ||x|-2|=a залежно від параметра а?

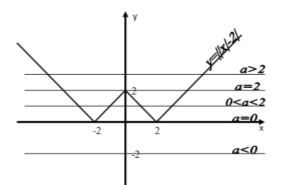
Будуємо графіки функцій у=||x|-2| та у=a.

З побудови видно:

1. Якщо a<0, то розв’язків немає.
2. Якщо a=0, то 2 розв’язки.
3. Якщо 0<a<2, то 4 розв’язки.
4.  Якщо a=2, то 3 розв’язки.
5. Якщо a>2, то 2 розв’язки.

 

Приклад 3. Скільки коренів має рівняння |х²-3|x|-4|=a залежно від параметра а?

Будуємо графіки функції

у=|х²-3|x|-4| та у=а у системі координат (х;у).

З побудови бачимо

1. Якщо a<0, то розв’язків немає.
2. Якщо a=0 і а=6,25, а>6,25, то 2 розв’язки (Якщо а=0, х=4, х=- 4).
3. Якщо 0<a<4, то 4 розв’язки.
4.  Якщо a=4, то 5 розв’язків.
5. Якщо 4<a<6,25, то 6 розв’язків.

 

Приклад 4. Розв’язати рівняння (х+1)|x-1|-a=0.

 Нагадаємо, що корені рівняння - це абсциси точок перетину графіків функцій у=f(x) і y=φ(x). Тому будуємо графіки функцій у=(х+1)|x-1| і у=a.

 Перший графік будуємо методом інтервалів, а другий графік – це пряма, паралельна осі абсцис. Перша функція має вигляд у=1-х² для х<1 і

у= х²-1 для х≥1.

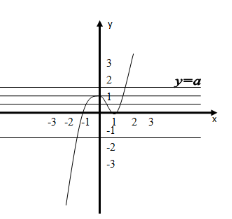Проведемо дослідження за графіком:

а<0, тоді пряма у=а перетне графік функцій у=1-х² в одній точці. Знайдемо абсцису цієї точки: 1-х²=а, х²=1-а, х=-;

а=0, точок перетину дві: х₁=-1; х₂=1;

0<а<1, точок перетину три: 1-х²=а,

х₁=-; х₂=; х²-1=а, х₃=;

а=1, тоді х₁=0, х₂==;

а>1, тоді х²-1=а, х=.

Відповідь.

х=-, якщо а є (-∞;0);

х_1,2=±1, якщо а=0;

х_1,2=±, х₃=, якщо 0<а<1;

х₁=0, х₂=, якщо а=1;

х=, якщо а є (1;+∞).

 

Приклад 5. Для яких значень параметра а рівняння (а+2х-х²)(а+|x-1|-1)=0  має рівно три розв’язки?  

Розв’язання :

 Дане рівняння рівносильне сукупності двох рівнянь:                                                          х²-2х =а,    і   1- |x-1| = a

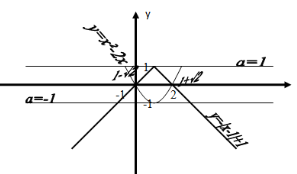  Побудуємо  графіки функцій y=х²-2х та y=-|x-1|+1

 З малюнка бачимо, що початкове рівняння має рівно три розв’язки, коли а= -1 (х=-1,  х=1, х=3)  або а= 1

 (,  х=1, , де  , та      корені рівняння    х²-2х =1)  

Відповідь: а= -1, а= 1.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ВИСНОВОК

 

Теоретичне вивчення явищ, процесів, застосування інформаційних технологій      приводять до розгляду загальних випадків існування залежностей між змінними, тобто до рівнянь, що містять параметри.

Отже, у даному посібнику я розглянула лінійні та квадратні рівняння з параметрами. Визначила, що параметр - це стала величина, але на даний момент є невідомою. Кожен тип рівнянь з параметрами має свій алгоритм розв’язування. Основними методами розв’язування є:

1. Аналітичний - це спосіб так званого прямого розв’язування, що повторює стандартні процедури знаходження відповіді в завданнях .
2. Графічний, коли при розв’язуванні розглядаються графіки  в координатній площині і визначається кількість розв’язків та їхні значення.                                                                   

Метою написання даного посібника  було поглибити знання і уміння по розв’язуванню рівнянь з параметрами, в яких використовується алгоритм розв’язування квадратного рівняння та властивості квадратичної функції.

Такі задачі найбільш відображають рівень математичного та логічного мислення, формують початкові навички дослідницької діяльності та математичну культуру.

Посібник  буде корисним  для учнів 8-11 класів загальноосвітніх шкіл, ліцеїв та гімназій як  для ознайомлення так і для  застосування набутих знань.                                   Учням знання по цій темі допоможуть скласти  зовнішнє незалежне оцінювання  з математики.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ВИКОРИСТАНА ЛІТЕРАТУРА

1. Апостолова Г.В., Ясінський В.В. Перші зустрічі з параметрами. – К., 2008.- 272с.
2. Вишенський В.О., Перестук М.О. Задачі з математики .- К., 1985. – 264 с.
3. Горнштейн П.І., Полонський В.Б., Якір М.С. Задачі з параметрами – К., 2004. – 254 с.
4. Коваленко В.Г., Кривошеєв В.Я., Старосєльцева О.В. Алгебра 9 клас. – Київ «Освіта», 1998. – 290с.
5. Кравчук О. Рівняння з параметрами . Газета «Математика» - № 13(361), квітень 2006- 17-24 с.
6. Кукарєкіна Т.М. Про підготовку випускників до вступних екзаменів у ВНЗ. Газета «Математика» - №23-24(275-276), червень 2004 -16-37с.
7. Лікоть В.В. Задачі з параметрами. – К., 2003- 258 с.
8. Нелін Є.П. Алгебра і початки аналізу. Підручник для 10 класу загальноосвітніх навчальних закладів. Профільний рівень. – Х.: Гімназія, 2010.-416с.
9. Репета В.К., Клешня Н.О. Задачі з параметрами – К., 2002- 264с.
10.  Рибачек. Л. Застосування властивостей квадратичної функції під час розв’язування рівнянь. Науково-методичний журнал «Математика в школах України»-№17-18(65-66)2004-25-28с.
11.  Рубан Е.А. Розв’язування рівнянь , систем рівнянь та нерівностей з параметрами.  Газета «Математика» - №24(228), черевень 2003.- 6-24с.
12. Сарана О.А. Ясінський В.В. Конкурсні задачі підвищеної складності з математики. К-.2005- 272 с.
13.  Ястребинецький Г.А. Рівняння й нерівності , що містять параметри. –К. 2004-258 с.