Урок "Властивості степеня з цілим показником"
Мета уроку:
- засвоєння учнями означення степеня з цілим від'ємним показником та його властивостей;
- формування вмінь та навичок застосовувати означення і властивості степеня з цілим показником для обчислення значень виразів та перетворення виразів із змінними;
- продовжити роботу з формування вмінь самостійно працювати з навчальною літературою та складати конспект;
- розвиток навичок усного підрахунку, логічного мислення, вмінь порівнювати, аналізувати і робити висновки, працювати в групі.
Тип уроку: урок засвоєння нових знань
АЛГЕБРА 8 КЛАС
СТЕПІНЬ З ЦІЛИМ ПОКАЗНИКОМ І ЙОГО
ВЛАСТИВОСТІ
(урок з використанням мультимедійної дошки)
Учитель: Холодних И.Н.
Тема уроку. Степінь з цілим показником і його властивості
Мета уроку:
- засвоєння учнями означення степеня з цілим від’ємним показником та його властивостей;
- формування вмінь та навичок застосовувати означення і властивості степеня з цілим показником для обчислення значень виразів та перетворення виразів із змінними;
- продовжити роботу з формування вмінь самостійно працювати з навчальною літературою та складати конспект;
- розвиток навичок усного підрахунку, логічного мислення, вмінь порівнювати, аналізувати і робити висновки, працювати в групі.
Тип уроку: урок засвоєння нових знань
Наочність та обладнання: підручник. Алгебра, 8 клас. Г. П. Бевз, В. Г. Бевз; збірник завдань і контрольних робіт з алгебри для 8 класу. Мерзляк А.Г., Полонский В. Б., Рабинович Е.М., Якир М. С.; конспект; роздавальний матеріал ("Скарбничка", диференційовані картки, картки з самостійною роботою)
Хід уроку
I. Організаційний етап (1 хвилина)
II. Перевірка домашнього завдання
Перевіряється наявність домашнього завдання впродовж уроку.
III. Актуалізація опорних знань (7 хвилин)
Диференційована робота на місцях (4-6 учнів)
 1. Одночасна Двоє учнів записують на дошці властивості робота степеня з натуральним показником
1. Одночасна Двоє учнів записують на дошці властивості робота степеня з натуральним показником
Фронтальне опитування за планом
План фронтального опитування
1) ![]() Означення степеня з натуральним показником.
Означення степеня з натуральним показником.
2) Множення степенів з однаковими основами.
3) Ділення степенів з однаковими основами.
4) Піднесення степеня до степеня. Слайд №1 5) Піднесення дробу до степеня.
6) Піднесення добутку до степеня.
7) Означення цілого числа.
8) Означення натурального числа.
Завдання для диференційованої роботи на місцях:
Картка високого рівня Картка основного рівня
|
1) a2 ∙ a3 2) a6 :a2 3) (a5)3 4) (a2)3 ∙ (a4)2 |
Обчисліть Спростити вираз
1) 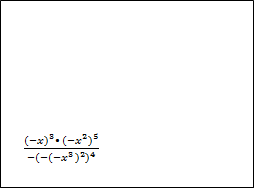 (-1)n • (-1)n • (-1)n • (-1)n Спростити вираз
(-1)n • (-1)n • (-1)n • (-1)n Спростити вираз
2) x3n – 1 : x3n – 2
3)
Після проведення фронтального опитування перевірити і прокоментувати властивості степеня з натуральним показником. Учні здають картки, перевірка впродовж уроку.
 33; (-5)2; 110;
33; (-5)2; 110;
2) Спростіть вираз:
a3 • a0 5 • 52 x : x a : a
Таким чином, наших знань про степінь замало. Розв’язання проблеми є одночасно й мотивацією і метою навчальної діяльності.
IV. Повідомлення теми, мети, епіграфа, структури уроку (2 хвилини). – слайд №3
Учитель: сьогодні накопичувальна система оцінки за урок (дидактична гра "Скарбничка"), кожен вид діяльності учнів на уроці оцінюється окремо.
Учні записують своє прізвище в "Скарбничку" .
Учитель: оцініть свою роботу на етапі актуалізації опорних знань.
Учні самостійно оцінюють свою роботу .
Учитель: "Хто заробив 1 бал"? Підніміть руку.
Слайд №4
|
«Скарбничка» _____________________________________ Прізвище, ім'я
|
V. Робота з підручником за планом, усна робота по складанню конспекта (8 хвилин)
План роботи за підручником (параграф 10)
1. ![]() Означення степеня з цілим показником.
Означення степеня з цілим показником.
2. Приклади застосування означення степеня з цілим показником.
3. Означення степеня з цілим показником для основи ![]() . Слайд №5
. Слайд №5
4. Приклади застосування означення степеня з цілим показником для основи ![]() .
.
5. Властивості степеня з цілим показником.
Учні знаходять у підручнику відповіді на питання. Аналізують властивості степеня з цілим від’ємним показником, порівнюнюють з властивостями степеня з натуральним показником, розглядають приклади застосування степеня з цілим від’ємним показником.
Скласти конспект вдома за зразком.
Конспект (зразок) – слайд №6
|
1. Означення степеня з цілим показником
Якщо a ≠ 0; n – натуральне число, то a-n = 2. Приклади: 1) 3-2 =
3. Означення степеня з цілим показником для основи
Якщо
4. Приклади:
3) 4) 0,7-2 =
5. Властивості степеня з цілим показником 1) am • an= am+n; 2) am : an= am-n; 3) (am)n= amn; 4) (ab)n= anbn; 5) 6) Если a ≠ 0, n ≠ 0, то a0 = 1, 0n = 0; 7) 00 – не имеет смысла. |
VI. Формування вмінь та навичок (13 хвилин)
1) Повернутися до завдання
![]() Подайте числа у вигляді степеня з основою 2: , , , .
Подайте числа у вигляді степеня з основою 2: , , , .
2) Розв’язання вправ біля дошки з коментуванням (гра «Ланцюжок» - беруть участь усі учні), охочі можуть працювати самостійно й заробляти бали.
Обов'язкове завдання за підручником: №458, №459
за збірником: №197 (1, 2, 3, 6, 7, 9)
№200 (5, 6, 10)
№201 (1, 2, 3)
Додаткове завдання за збірником: №201 (6) 1б
№200 (13) 1б
№200 (15) 1б
1. Обов’язкове завдання:
- за підручником:
№458. Замініть степінь з цілим від’ємним показником дробом:
а) 2–3 б) 3–2 в) 77–1
г) b–3 д) (xy) –3 e) (m – n) –2
№459. Замініть дріб степенем з цілим від’ємним показником:
![]()
![]()
![]() а) б) в)
а) б) в)
г) д) e)
- за збірником:
№197. Обчисліть:
1) 12–2 2) 3–4 3) (–2)–6
6) ![]() 7)
7) ![]() 9)
9) ![]()
№200. Подайте вираз у вигляді степеня або добутку степенів :
5) a9 : a –3 6) a –4 : a –12 10) (a3) –7 ∙ (a –4)–5 : (a –5)8
№201. Знайти значення виразу:
1) 75 ∙ 7–7 2) 10–12 ∙ 1015 3) 5–12 : 5–16
Додаткове завдання за збірником:
№201. Знайти значення виразу: 6) ![]()
№200. Подайте вираз у вигляді степеня або добутку степенів:
13) (a 2 b –3)–3 ∙ (a –4 b 9) 6 15) ![]()
Учитель перевіряє та коментує роботу учнів біля дошки та самостійну роботу в зошитах.
Після виконання обов’язкових завданнь учні самостійно оцінюють свою роботу на цьому етапі.
Учитель: «Хто заробив 2 бали? Підніміть руку».
«Хто заробив 1 бал? Підніміть руку».
«Хто не отримав оцінки з цього виду роботи? Підніміть руку».
VII. Самостійна робота (4 хвилини) (Первинний контроль. Перевірити рівень засвоєння учнями означення та властивостей степенів з цілим показником)
Слайд №7
|
I варіант _____________ |
|
II варіант ____________ |
|
№1. Заповнити пропущене |
|
№1. Заповнити пропущене |
|
1) 9-2 = 2) |
|
1) 2-3 = 2) |
|
3) 4) (-3)-4 = 5) a15 • a-4 = a… 0,5б |
|
3) 4) (-2)-5 = 5) b10 • b-6 = b… 0,5б |
|
6) (m-5)-6 = m… 0,5б
|
|
6) (c-4)-3 = c… 0,5б |
|
№2. Обчисліть |
|
№2. Обчисліть |
|
1) 5-2 = 1б |
|
1) 3-2 = 1б |
|
2) 45 : 46 = 1б |
|
2) 89 : 810 = 1б |
VIII. Групова робота - взаємоперевірка самостійної роботи за зразком (3 хвилини) Виставляння балів за самостійну роботу.
Слайд №8
|
I вариант |
|
II вариант |
|
№1. Заполнити пропущене |
|
№1. Заполнити пропущене |
|
1) 92 0,5б |
|
1) 23 0,5б |
|
2) -3 0,5б |
|
2) -4 0,5б |
|
3) 3 0,5б |
|
3) 2 0,5б |
|
4) |
|
4) |
|
5) 9 0,5б |
|
5) 4 0,5б |
|
6) 30 0,5б |
|
6) 12 0,5б |
|
№2. Обчисліть 1) 5-2 = 2) 45 : 46 = |
|
№2. Обчисліть 1) 3-2 = 2) 89 : 810 = |
IX. Підведення підсумків уроку (5 хвилин)
1. Що нового дізналися на уроці? (Існує степінь з цілим показником)
2. Які властивості мають степені з цілими показниками?
(Перерахувати)
3. Сформулювати алгоритм обчислення степеня з цілим від’ємним показником.
4. Виставити бали за активну роботу на уроці, за розв’язання додаткових завдань.
5. Заповнити і здати "Скарбничку", картку з самостійною роботою.
X. Домашнє завдання (2 хвилини) – слайд №9
1) Параграф 10, написати і вивчити конспект.
2) Розв’язати за підручником: №460 (в, г), №461, №463.
3) Підготуватися до математичного диктанту, фронтального опитування.
Відповіді
1. Картка високого рівня
1) 1
2) x
3) ![]()
2. Картка основного рівня
1) додають
2) віднімають
3) множать, залишають
4) множник
5) множать
1. Обов’язкове завдання:
- за підручником:
№458. Замініть степінь з цілим від’ємним показником дробом:
![]()
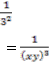 а) 2–3 = б) 3–2 = в) 77–1 =
а) 2–3 = б) 3–2 = в) 77–1 = ![]()
г) b–3 = д) (xy) –3 e) (m – n) –2 = ![]()
№459. Замініть дріб степенем з цілим від’ємним показником:
![]()
![]()
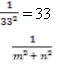 а) = 5-1 б) = 7-3 в) -2
а) = 5-1 б) = 7-3 в) -2
г) = (ab)-1 д) = x-9 e) = (m2 + n2)-1 - за збірником:
№197. Обчисліть:
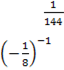
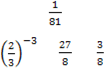
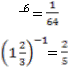 1) 12–2 = 2) 3–4 = 3) (–2)
1) 12–2 = 2) 3–4 = 3) (–2)
6) = -8 7) = = 3 9)
№200. Подайте вираз у вигляді степеня або добутку степенів :
5) a9 : a –3 = a6 6) a –4 : a –12 = a8 10) (a3) –7 ∙ (a –4)–5 : (a –5)8 = a39
№201. Знайти значення виразу:
1) 75 ∙ 7–7 = ![]() 2) 10–12 ∙ 1015 = 1000 3) 5–12 : 5–16 = 625
2) 10–12 ∙ 1015 = 1000 3) 5–12 : 5–16 = 625
Додаткове завдання за збірником:
№201. Знайти значення виразу: 6) ![]() = 1
= 1
№200. Подайте вираз у вигляді степеня або добутку степенів:
13) (a 2 b –3)–3 ∙ (a –4 b 9) 6 = a-30 b63 15) ![]()


про публікацію авторської розробки
Додати розробку
