Урок "Властивості та графік логарифмічної функції"
ТЕМА: Властивості та графік логарифмічної функції.
МЕТА: Ввести поняття логарифмічної функції, формувати вміння будувати графік логарифмічної функції, з’ясувати властивості логарифмічної функції. Виховувати наполегливість у досягненні мети, акуратність. Розвивати увагу, пам’ять, спостережливість, уміння робити висновки, спираючись на відомі факти.
Структура уроку
1. Перевірка домашнього завдання.
2. Актуалізація опорних знань.
3. Мотивація навчання.
4. Властивості та графік логарифмічної функції.
5. Розв’язування вправ.
6. Домашнє завдання.
7. Підсумок уроку.
Хід уроку
1. Перевірка домашнього завдання
Перевірка виконання деяких вправ домашньої роботи (Декілька студентів працюють біля дошки).
Фронтальне опитування інших студентів з теорії :
1. Що називається логарифмом?
2. Які види логарифмів ви знаєте?
3. Назвіть властивості логарифмів.
2. Актуалізація опорних знань
Математичний диктант
|
І варіант |
ІІ варіант |
|
1. Обчислити: 𝑙𝑜𝑔381; 𝑙𝑜𝑔7343; 𝑙𝑛𝑒; 𝑙𝑔1000; 𝑙𝑔0,001; 𝑙𝑜𝑔136. 6 |
1. Обчислити: 𝑙𝑜𝑔464; 𝑙𝑜𝑔9729; 𝑙𝑛1; 𝑙𝑔10000; 𝑙𝑔0,01; 𝑙𝑜𝑔149. 7 |
|
2. Обчислити: 3𝑙𝑜𝑔327 𝑙𝑜𝑔432 + 𝑙𝑜𝑔42; 𝑙𝑜𝑔3108 − 𝑙𝑜𝑔34; 𝑙𝑜𝑔552; 𝑙𝑜𝑔2(8 ∙ 128). |
2. Обчислити: 4𝑙𝑜𝑔4256; 𝑙𝑜𝑔432 + 𝑙𝑜𝑔48; 𝑙𝑜𝑔336 − 𝑙𝑜𝑔34; 𝑙𝑜𝑔514; 𝑙𝑜𝑔5(25 ∙ 125). |
|
4. Записати показникову рівність у вигляді логарифмічної: |
4. Записати показникову рівність у вигляді логарифмічної: |
|
36 = 729; 104 = 10000
|
45 = 1024 10−3 = 0,001
|
|
5. Записати логарифмічну рівність у вигляді показникової: |
5. Записати логарифмічну рівність у вигляді показникової: |
|
𝑙𝑜𝑔381 = 4; 𝑙𝑔0,01 = −2 |
𝑙𝑜𝑔5125 = 3; 𝑙𝑔100000 = 5 |
Фронтальне опитування
1. Яку функцію називають оборотною?
2. Як можна задати функцію, обернену до даної?
3. Сформулювати основні властивості взаємно обернених функцій.
4. Назвати властивості показникової функції.
5. Зобразити схематично у різних системах координат графіки показникових функцій при основі a > 1 і 0 < a < 1.
3. Мотивація навчання
Вам уже знайоме ім’я математика Ейлера. Виклавши деякі властивості показникової функції, він помітив, що, маючи залежність 𝑦 = 𝑎𝑧, можна розглянути показник z як функцію y, яку й називають логарифмічною функцією з основою a. Сьогодні ми приступимо до вивчення саме цієї функції.
4. Властивості та графік логарифмічної функції
Функцію, задану формулою 𝑦 = 𝑙𝑜𝑔𝑎𝑥, де 𝑎 > 0і 𝑎 ≠ 1, називаютьлогарифмічною.
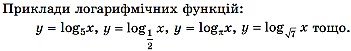
Логарифмічна функція за своїм означенням є оберненою до функції 𝑦 = 𝑎𝑥. А графіки двох взаємно обернених функцій симетричні відносно прямої 𝑦 = 𝑥. Таким чином, графіки показникової функції 𝑦 = 𝑎𝑥 і логарифмічної функції 𝑦 = 𝑙𝑜𝑔𝑎𝑥, що мають однакові основи а, симетричні відносно прямої 𝑦 = 𝑥.
Побудуємо графіки функцій 𝑦 = 𝑙𝑜𝑔𝑎𝑥, де 𝑎 > 1 і 𝑦 = 𝑙𝑜𝑔𝑎𝑥, де 0 < 𝑎 < 1, у тих системах координат, де побудовано графіки відповідних показникових функцій.
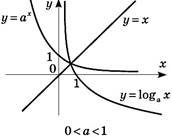
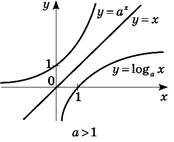
Властивості логарифмічної функції описуються студентами за графіком, одночасно заповнюється таблиця.
|
№ з/п |
Функція 𝑦 = log𝑎 𝑥 |
|
|
0 < 𝑎 < 1 |
𝑎 > 1 |
|
|
1 |
D(y) = (0; ∞) |
D(y) = (0; ∞) |
|
2 |
E(y) = R |
E(y) = R |
|
3 |
Нулі функції: у=0 при х=1. |
Нулі функції: у=0 при х=1. |
|
4 |
Монотонність: спадає |
Монотонність: зростає |
|
5 |
|
|
|
6 |
|
|
5. Розв’язування вправ
Підручник: Істер О.С. Математика (алгебра і початки аналізу та геометрія, рівень стандарту): підруч. для 11-го кл. закл. заг. сер. освіти / О.С. Істер – Київ: Генеза, 2018. – 384 с.: іл.
Розв’язуємо номери: 5.1 (усно), 5.3, 5.5, 5.7, 5.11, 5.13, 5.15, 5.31, 5.37.

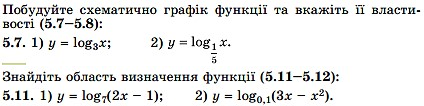
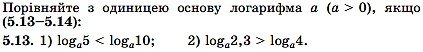
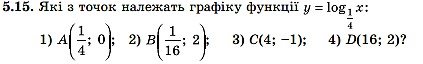
![]()
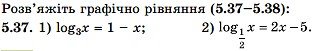
6. Домашнє завдання
Номери – 5.2, 5.4, 5.12, 5.14, 5.16, 5.32.
7. Підсумок уроку
Викладач відповідає на питання студентів. Нагадує основні задачі, які було розглянуто на занятті.


про публікацію авторської розробки
Додати розробку