Урок "Вписані чотирикутники. Описані чотирикутники"
Пропонується розробка уроку геометрії для 8-го класу "Вписані чотирикутники. Описані чотирикутники". Містить теоретичний матеріал та підбірку практичних завдань.
Урок математики з теми:
«Вписані чотирикутники. Описані чотирикутники»
Урок: геометрії
Клас: 8
Тема: «Вписані чотирикутники. Описані чотирикутники»
Мета: працювати над засвоєнням учнями змісту понять: чотирикутник, вписаний у коло; чотирикутник описаний навколо кола; розглянути зміст теорем про вписаний та описаний чотирикутник та схеми їх доведення; розвивати логічне і абстрактне мислення; сприяти вихованню культури мови і спілкування.
Тип уроку: урок засвоєння знань, умінь та навичок.
Наочність та обладнання: схема вписаний і описаний многокутники.
Формування вміння:
- відтворювати вивчені твердження;
- виконувати рисунки за описом;
- використовувати вивчені теореми піл час розв'язування задач на чотирикутники.
- Організаційний етап.
- Перевірка домашнього завдання.
Бесіда за готовими рисунками на розуміння учнями обґрунтування основних етапів розв'язання
задач.
- Формування мети і завдань уроку.
(Схема-логіка побудови курсів геометрії в 7-му та 8-му класах)
За схемою визначити місце сьогоднішнього уроку, сформулювати основну мету уроку - вивчення питань про спосіб визначення поняття чотирикутника, вписаного в коло та описаного навколо кола; з'ясування можливостей вписати чотирикутник у коло або описати чотирикутник навколо кола та необхідних й достатніх умов, за яких це можна зробити.
IV. Актуалізація опорних знань.
Виконання усних вправ за готовими рисунками.
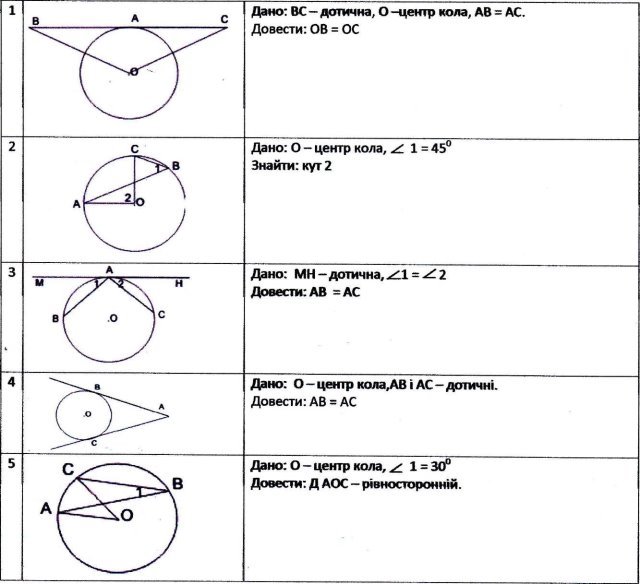
V. Засвоєння нових знань (евристична бесіда)
План.
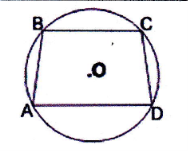
- Означення чотирикутника вписаного в коло.
- Теорема про вписаний чотирикутник.
- Наслідки з теореми про вписаний чотирикутник.
- Означення описаного чотирикутника.
- Теорема про описаний чотирикутник.
- Наслідки з теореми про описаний чотирикутник.
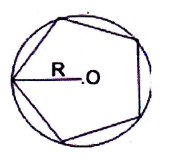
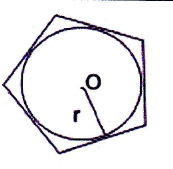
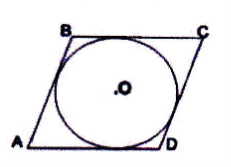
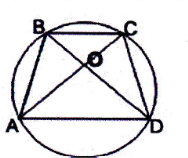
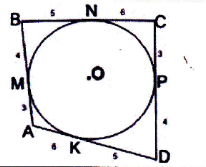
![]() Тільки у випадку, коли всі вершини (сторони) чотирикутника лежать на колі (дотикаються до кола), даний чотирикутник буде називатися вписаним у коло (описаним навколо кола).
Тільки у випадку, коли всі вершини (сторони) чотирикутника лежать на колі (дотикаються до кола), даний чотирикутник буде називатися вписаним у коло (описаним навколо кола).
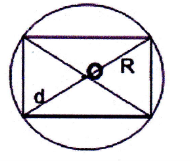
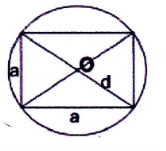
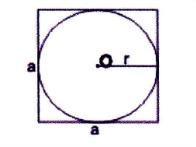
- Вершини чотирикутника, вписаного в коло, рівновіддалені від центра кола; відрізок, що з'єднує центр кола з будь якою вершиною, є радіусом кола.
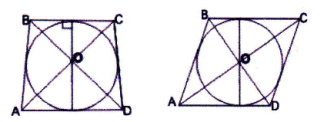
- Для чотирикутника, описаного навколо кола, рівновіддаленими від центра кола будуть сторони, тобто перпендикуляр, проведений із центра кола, вписаного в чотирикутник, до сторони чотирикутнику, і е радіусом цього кола.
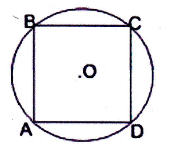
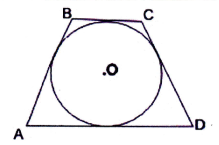
Завдання. На якому із наведених рисунків зображено чотирикутник АВСО: а) вписаним у коло; б) описаним навколо кола?
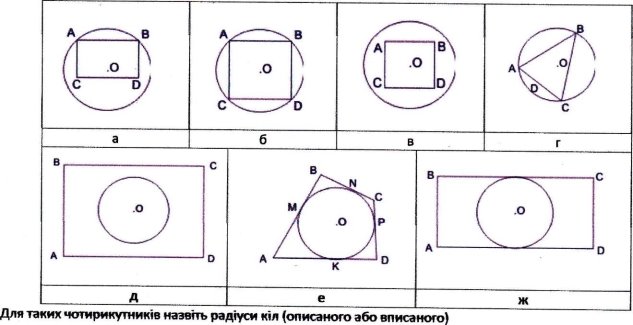
Виконання усних вправ.
245.У який прямокутник можна вписати коло? Навколо якого ромба можна описати коло?
246.Чи можна описати коло навколо чотирикутника, який має лише один прямий кут?
Опорні задачі.
255. Центр кола, описаного навколо прямокутника, є точкою перетину його діагоналей. Доведіть.
265. а) Центр кола, вписаного в ромб, є точкою перетину його діагоналей. Доведіть.
б) Радіус кола, вписаного в трапецію, дорівнює половині її висоти. Доведіть. Укладання опорного конспекту.
Робота в групах з узагальненням досягнень всіх груп над питанням про положення центра вписаного (описаного кола та співвідношення між елементами (сторонами, висотами) чотирикутників та радіусом вписаного (описаного) кола.
Вписаний і описаний многокутники
(вписане і описане коло).
|
|
|
|
Вписаний – усі вершини лежать на колі |
Sопис = Де Р – периметр, r – радіус вписаного кола |
Вписаний та описаний чотирикутники.
|
|
|
|
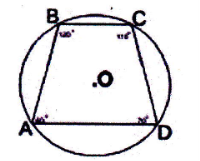
∠А + ∠С=180° ∠В + ∠D=180° І навпаки: якщо сума протилежних кутів Чотирикутника дорівньє 180, то навколо нього можна описати коло. |
∠AB + ∠CD=DC+AD (суми довжин протилежних сторін рівні) І навпаки: якщо суми протилежних сторін випуклого чотирикутника рівні, то в нього можна вписати коло. |
Трикутник
|
|
то він прямокутник.
|
Трапеція і ромб
|
|
|
|
Якщо ABCD – вписана трапеція, то AB=CD |
dвпис.кола = h O- точка перетину бісектрис внутрішніх кутів ∠AOB = ∠COD = 90° |
Квадрат
|
|
|
|
|
|
VI. Формування первинних умінь. Виконання усних вправ.
- Чи можна описати коло навколо прямокутної трапеції?
- У трапеції три сторони рівні. Чи можна в таку трапецію вписати коло? Чи можна навколо такої трапеції описати коло?
Виконання письмових вправ.(Робота в групах)
- Визначте, чи можна описати коло навколо чотирикутника ABC D, якщо кути А, В, С, D дорівнюють відповідно: а) 90°, 90°, 20°, 160°;
б) 5°, 120°, 175°, 60°.
- 2. Знайдіть невідомі куги:
а) вписаного чотирикутника, якщо два з них дорівнюють 46° і 125°;
б) вписаної трапеції, якщо один із них дорівнює 80°;
в) вписаного чотирикутника, діагоналі якого точкою перетину діляться навпіл.
- Знайдіть периметр:
а) описаного чотирикутника, три послідовні сторони якого дорівнюють 7 см, 9 см і 8
см;
б) описаної трапеції, бічні сторони якої дорівнюють 3 см і 11 см.
- Рівнобедрена трапеція описана навколо кола. Знайдіть середню лінію трапеції, якщо її бічна сторона дорівнює 7 см.
- Діагональ ромба, що виходить з вершини кута 60°, дорівнює 24 см. Знайдіть радіус кола вписаного в ромб.
VII. Підсумки уроку.
Злови помилку.
|
1.
|
2. AB = 5 см, BC = 5,5 см.
|
|
|
4.
|
VIII. Домашнє завдання.
§8, домашня самостійна робота.
-
 У трикутнику ABC точки М і N- середини сторін АВ і ВС відповідно. Периметр трикутника ABC дорівнює 22 см. Знайдіть периметр трикутника MBN.
У трикутнику ABC точки М і N- середини сторін АВ і ВС відповідно. Периметр трикутника ABC дорівнює 22 см. Знайдіть периметр трикутника MBN.
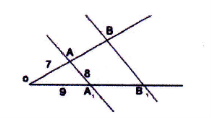
- На рисунку
∠АВВ1 + ∠А1АВ= 180°.
Знайдіть периметр
чотирикутника ABВ1А1.
- Знайдіть кути рівнобедреного трикутника, основа якого стягує п'яту частину дуги описаного кола. Розгляньте всі можливі випадки.


про публікацію авторської розробки
Додати розробку