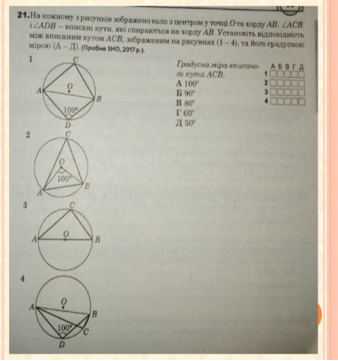
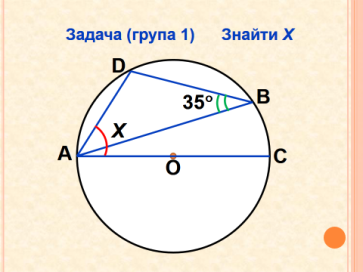
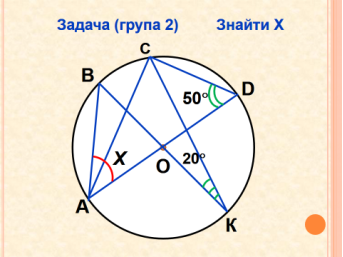
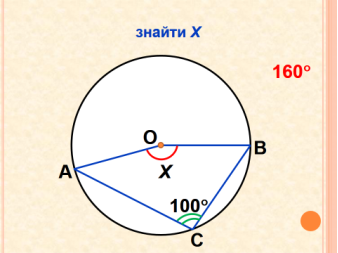
Урок "Вписані і центральні кути"

Тема уроку: Центральні та вписані кути. Розв’язування задач.

Мета уроку:

•         навчальна  (формування предметних компетентностей):  сформувати вміння застосовувати означення вписаних і центральних кутів, теорему про вписаний кут і наслідки з неї до розв’язування задач; знаходити на готовому рисунку вивчені поняття; виконувати правильні зображення вивчених понять заданим описом; розв'язувати задачі із використанням вивчених тверджень на обчислення градусної міри вписаних та центральних кутів; перевірити результати засвоєння учнями цих вмінь;
•         розвивальна (формування ключових компетентностей): розвивати математичну мову, уяву, логічне мислення, вміння аналізувати, порівнювати розвивати прагнення до самостійного, творчого підходу при розв'язанні нестандартних завдань, вміння узагальнювати й конкретизувати властивості вивчених об’єктів і застосовувати  їх  до розв’язування задач, сприяти розвитку вміння критично мислити, висловлювати і доводити свою думку, слухати і чути інших, оцінювати, аргументувати та змінювати думку на основі доказів, ухвалювати аргументовані рішення в життєвих ситуаціях, співпрацювати в команді, виділяти та виконувати власну роль у командній роботі.
•    виховна (соціальна та громадянська компетентності): виховувати культуру спілкування, любов до предмета, виховувати графічну культуру, культуру усного математичного  мовлення. 

Тип уроку: урок застосування знань, умінь і навичок

Методи і прийоми: словесний (бесіда, робота з підручником), наочний (спостереження, демонстрація),  практичний (креслення геометричних фігур), елементи пошуково-проблемного,  усний рахунок (розв’язування задач за готовими рисунками), міжпредметні зв’язки, «практичність теорії», «емоційний термометр» (рефлексія), «приваблива мета», «взаємоперевірка» , «лови помилку», гра – « так» - «ні».

Форми роботи: індивідуальна, групова, робота в парах, колективна.

Обладнання: підручник, презентація, роздатковий матеріал, креслярські інструменти.

Дата проведення: 12.11.20

Клас : 8 – А

Вчитель: Тринчук О.Л.

ХІД УРОКУ

І. Організаційний етап.

  Доброго дня! Я бачу розумні оченята, які прагнуть пізнавати нове. Рада всіх бачити! І з задоволенням проведу урок геометрії для вас. А щоб урок був цікавим і результативним, пропоную провести його під девізом:

Не просто слухати, а чути.

Не просто дивитися, а бачити.

Не просто відповідати, а міркувати.

Дружно і плідно працювати…

II. Актуалізація опорних знань і вмінь.

Діти, перед вами лежать листи самооцінювання, які ви будете заповнювати напротязі уроку і потім здасте мені для виставлення оцінок.

1. Перевірка домашнього завдання, заданого за підручником.  (Відповіді на слайді. Взаємоперевірка).

2. Фронтальне опитування. П-П-П ( Робота в парах: учні повторюють означення, теореми – проговорюють один одному – відповідають на запитання). Запитання на слайді.

1. Який кут називають вписаним?

2. Який кут називають центральним?

3. Чому дорівнює градусна міра дуги кола?

4. Властивості вписаного кута?

5. Наслідки з теореми про вписаний кут?

ІІІ. Мотивація навчальної діяльності. Формулювання теми,  мети уроку,

Ви знаєте, що будь - які знання набувають для того, щоб застосовувати їх на практиці. (Проблемна ситуація). Уявіть собі, що вам потрібно знайти центр круга, виготовленого із паперу (учні згинаючи круг, знаходять центр). Уявіть собі,  що вам потрібно знайти центр круга, виготовленого із фанери, або – центр круга на площині. Як бути? У вас є косинець. Як користуючись косинцем, знайти центр круга?

Відповідь: Потрібно скористатися одним із наслідків з теореми про вписаний кут. Оскільки центром описаного навколо прямокутного трикутника, є середина гіпотенузи, то можна цей косинець двічі вписати в круг і знайти точку перетину найбільших сторін, тобто гіпотенуз.

Сьогодні на уроці ми продовжимо працювати над темою центральні та вписані кути. Будемо застосовувати означення вписаних і центральних кутів, теорему про вписаний кут і наслідки з неї до розв’язування задач. Мета уроку – навчитися визначати вписані і центральні кути та застосовувати їх властивості при розв’язуванні задач.

ІV.  Застосування знань. Удосконалення вмінь.

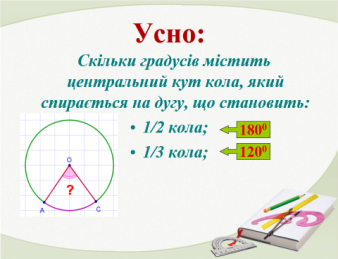
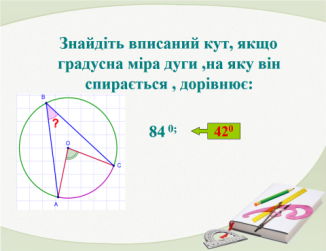
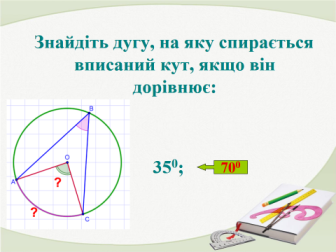
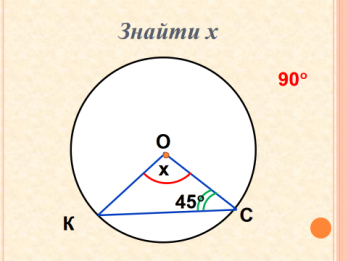
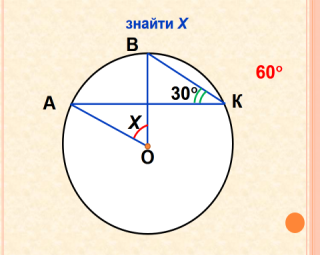
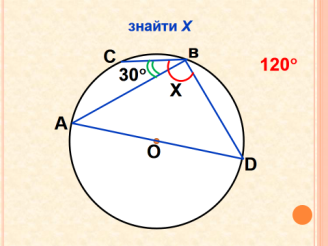
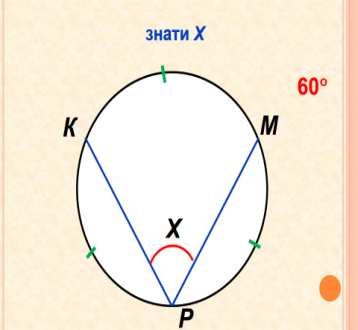
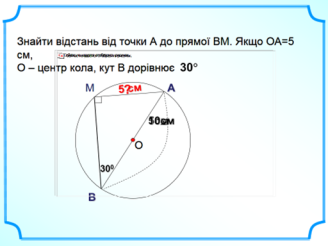
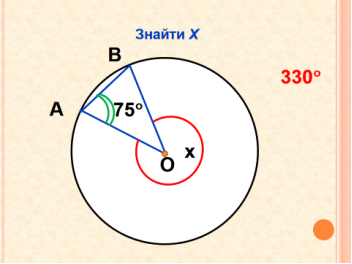
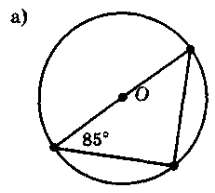
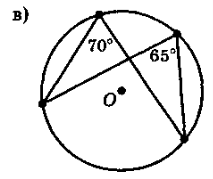
1. Розв’язування задач за готовими рисунками ( усний рахунок, колективна робота).   Слайди 17-26

2. Робота в групах (письмово; задачі на готових ватманах, учні розв’язують, а потім представник демонструє розв’язання, )

 V. Підбиття підсумків уроку .

1. Знайдіть помилки на рисунках («лови помилку»)

Графічний диктант. Вписані та центральні кути. «Так, чи ні?»

1. Центральним кутом у колі називається кут з вершиною на колі?  (ні)
2. Градусна міра дуги кола – це градусна міра відповідного центрального кута? (так)
3. Градусна міра півкола становить 180°?  (так )
4. Градусна міра дуги всього кола 270°?  (ні)
5. Вписаний кут – кут з вершиною на колі, сторони перетинають коло? (так)
6. Вписаний кут вимірюється дугою, що на неї спирається ?  (ні)
7. Вписаний кут дорівнює половині центрального кута, що спирається на одну і ту ж дугу ?  (так)
8. Вписані кути , що спираються на одну й ту ж дугу, рівні?   (так)
9. Вписаний кут, що спирається на півколо, розгорнутий?   (так)
10. Якщо дуга менша за півколо, то вписаний кут гострий?    (так)
11. Якщо дуга більша за півколо, то вписаний кут тупий?  (так)
12. Центральний кут 120°, то вписаний кут, що спираються на відповідну дугу, 100°? (так)

VI. Рефлексія

Оберіть смайлик, що відповідає вашому настрою.

VIІ. Домашнє завдання

Повторити  п. 11  №  11.8; №  11.11.

Творче завдання: скласти задачі за готовими малюнками.  Всі задачі, які ви склали ви повинні уміти розв’язувати.