Урок з алгебри у 9 класі на тему"Узагальнення та систематизація вивченого про квадратичну функцію."
Тема: Узагальнення та систематизація вивченого про квадратичну функцію.
Мета: Повторити вивчене про квадратичну функцію, її використання при розв’язуванні нерівностей, вправ з використанням графіків.
Тип уроку: урок узагальнення і систематизації.
Обладнання: комп’ютерна презентація, роздатковий матеріал.
Хід уроку
І. Організаційна частина.
1) Організація класу;
2) Оголошення епіграфа уроку:
„Знати – це означає насамперед
уміти користуватися знаннями”
В. О. Сухомлинський
ІІ. Мотивація навчальної діяльності, повідомлення теми, мети і завдань уроку.
ІІІ. Актуалізація опорних знань.
а) Фронтальна бесіда з метою виявлення рівня теоретичних знань.
Яка функція називається квадратичною?
Що є графіком квадратичної функції?
З чого складається парабола?
Як може розміщуватися парабола?
За якою формулою обчислюється вершина параболи?
При використанні яких властивостей потрібна вершина, її координати?
Де функція набуває додатніх, від’ємних значень?
Що таке нулі функції?
Де використовують нулі функції?
б) Математична розминка (усні вправи з використанням таблиці з графіками функцій).
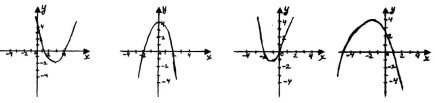
1. Графіки яких функцій схематично зображені на малюнках? Поясни чому.
2. Вказати проміжки зростання і спадання функцій на даних малюнках.
3. Вказати області значень функцій.
4. Де функція набуває додатних значень, від’ємних значень?
в) Перевірка домашнього завдання, вправами аналогічними до домашніх:
1 уч. Побудувати графіки функцій за допомогою шаблона
y=-2(х+4)2
y=2х2+2
(виконати самостійно)
2 уч. Знайти нулі функції y=6х2-7х+2
(виконати самостійно)
(D=1, x1=
, х2=
).
3 уч. Знайти область значень і проміжки зростання і спадання функції (працює з класом) y=-х2+6х+5
(вершина: m=3, n=14, (3;14))
IV. Тренувальні вправи.
Робота з таблицями сторінка 109.
1) №3 (е) розв’язати нерівність
3х(2х-1)<2х2-10х+2 (х є (-2; 
))
2) № 6 (б) Знайти область визначення функції
у=
(D (у): х є [(-1; 1) u (1; 2)]
3) Самостійна робота(завдання по рядах, ”Хто швидше? ”).
1 ряд: нулі функції y=3х2+4х-7
(D=100; х1=1; х2= -2
)
2 ряд: область значення функції y=х2-10х+1
((5;-24); Е (у): у є (-24; ∞)).
3 ряд: проміжки зростання і спадання функції y=-2х2+8х-1
((2; 7), зрост. (-∞; 2), спад (2; +∞))
Індивідуальне завдання найслабшим учням:
Знайти нулі функції y=х2-6х+8
(виконання за зразком y=х2-10х+9)
V. Хвилина відпочинку.
Приклади застосування квадратичної функції (два учні самостійно готували інформацію).
1) Застосування на уроках фізики – формула шляху рівноприскореного руху
S=
+v0t+b; S=
.
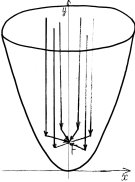
2) Застосування в техніці – фігури параболоїда, отриманого з обертання параболи навколо осі Y.
Якщо параболу обернути навколо осі ординат, то утвориться чаша. Щоб вона не була нескінченою, відріжемо частину її площиною, перпендикулярною до осі ординат. Утвориться фігура, яку називають параболоїдом. Якщо тепер зробити внутрішню поверхню параболоїда дзеркальною і направити потік світла у напрямі осі ординат, то всі промені світла зберуться в одній точці, яку називають фокусом. А якщо у фокусі поставити джерело світла, то одержимо звичайну фару або ліхтарик.
VI. Підсумок уроку.
Відповіді на запитання вчителя з використанням кросворду.
1.Залежність однієї змінної від другої називається . . . функція.
2. Значення х, при яких функція перетворюється в нуль,називається . . . нуль функції.
3.Функція виду y=ax2+bx+c називається . . . квадратична.
4. Якщо більшому значенню аргументу відповідає менше значення функції, то функція . . . спадна.
5. Множина всіх значень Y називається . . . областю значень.
6. Графіком квадратичної функції є . . . парабола.
7. Незалежна змінна функції називається . . . аргумент.
8. Основний елемент графіка квадратичної функції . . . вершина.
9. Від коефіцієнта а залежить розміщення . . . вітки.
10. Фігуру, яку отримують в результаті обертання параболи навколо осі Y, називають . . . параболоїд.
VII. Домашнє завдання.
Підготуватись до тематичного оцінювання.
про публікацію авторської розробки
Додати розробку