Геометрія 10 клас

Розділ. КООРДИНАТИ І ВЕКТОРИ.

Тема: Кут між векторами

(Матеріали для проведення уроку з геометрії 10 клас, на основі підручника Математика 10 клас автор Бевз)

 

1.     Скалярний добуток векторів

                Скалярним добутком векторів                         ⃗                     називають число 𝑥₁𝑥₂ +

𝑦₁𝑦₂ + 𝑧₁𝑧₂.

Приклад 1. Знайти скалярний добуток векторів 𝑎⃗(−4; 1; 3)та 𝑏⃗⃗(2; 6; 5).

.

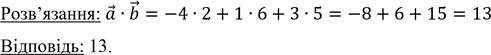2.     Кут між векторами

Кутом між двома ненульовими векторами називається кут між нарямами цих векторів.

Кутом між двома ненульовими векторами, що не мають спільного початку називають кут між векторами, що дорівнюють даним і мають спільний початок.

     ⃗𝒂⃗⃗

 

                                                                                                                                    

                                                                 ⃗𝒃⃗⃗

Кут між співнапрямленими векторами дорівнює нулю,

           

                              𝑎⃗

                                              𝑏⃗⃗

кут між протилежно напрямленими векторами дорівнює 180°.  𝑎⃗      180°                   𝑏⃗^⃗

       

1. Теорема про скалярний добуток векторів.

Скалярним добутком двох ненульових векторів називається число, яке дорівнює добутку числових значень довжин цих векторів і косинус кута між векторами:

.

 

Наслідок 1. Якщо вектори перпендикулярні, то їх скалярний добуток дорівнює нулю.

Наслідок 2. Якщо скалярний добуток векторів дорівнює нулю, то вони перпендикулярні.

Якщо з двох векторів хоча б один нульовий, то їх скалярний добуток дорівнює нулю.

Кут 𝜑між ненульовими векторами 𝑎⃗ = (𝑥₁; 𝑦₁; 𝑧₁), 𝑏⃗⃗ = (𝑥₂; 𝑦₂; 𝑧₂) можна визначити за формулою

 

𝑥1𝑥2 + 𝑦1𝑦2 + 𝑧1𝑧2 cos 𝜑 =

√𝑥12 + 𝑦12 + 𝑧12 ∙ √𝑥2 + 𝑦2 + 𝑧2

                                                                                                                                             2           2            2

№1356

а)  ⃗𝑎⃗⃗⃗ ∙ 𝑏⃗⃗ = 1 ∙ (−8) + 2 ∙ 2 + (−3) ∙ 4 = −8 + 4 − 12 = −16

б)  ⃗𝑚⃗⃗⃗⃗ ∙ 𝑛⃗⃗ = (−2) ∙ 2 + (−3) ∙ 3 + 2 ∙ 0,5 = −4 − 9 + 1 = −12

в)  ⃗𝑝⃗⃗⃗ ∙ 𝑘⃗⃗ = (−3) ∙ (−2) + (−7) ∙ 10 + 1 ∙ (−6) = 6 − 70 − 6 = −70

г)  ⃗𝑐⃗⃗ ∙ 𝑑⃗ = 4 ∙ 2 + (−2) ∙ 3 + 3 ∙ (−10) = 8 − 6 − 30 = −28

 

№1359

а)  Спочатку знайдемо косинус кута між векторами за формолою:

 

 

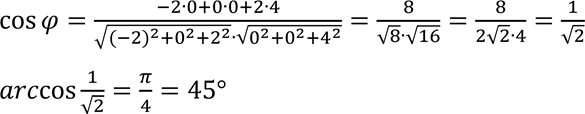
Відповідь:

б)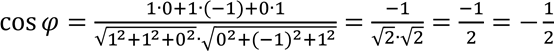 

 

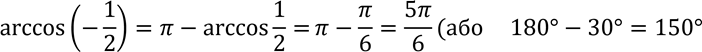
Відповідь:

в)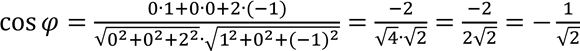 

 

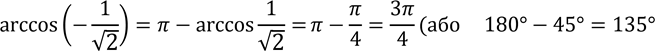
Відповідь:

г) 

 

Відповідь:

Домашнє завдання:  §37 вивчити основні поняття та формули Виконайте № 1358