Урок з геометрії 7 клас "Коло. Круг"

Урок 37

Коло. Круг

Мета:

навчальна: домогтися засвоєння означень кола, круга та їх елементів; сформувати вміння знаходити ці елементи на рисунку та виконувати рисунок за поданим описом, використовувати означення кола та його елементів під час розв’язування задач;

розвивальна: формувати вміння грамотно формулювати власні думки; розвивати увагу, пам’ять;

виховна: виховувати наполегливість у досягненні мети, старанність, уважність.

Тип уроку: засвоєння нових знань і вмінь.

Обладнання: набір демонстраційних креслярських інструментів, конспект 19.

Хід уроку

І. Організаційний етап

Учитель перевіряє готовність учнів до уроку, налаштовує їх на роботу.

ІІ. Перевірка домашнього завдання

Учитель збирає зошити з виконаним аналізом контрольної роботи, відповідає на можливі запитання учнів.

ІІІ. Формулювання мети і завдань уроку

Із метою створення мотивації навчальної діяльності учнів можна звернутися до попереднього досвіду учнів, а саме: нагадати їм про те, що ознайомлення з геометричними фігурами відбулося в учнів досить давно (ще в початковій школі). Серед фігур, відомих учням ще з початкової школи, окремо стоїть одна, несхожа на інші фігури — це коло. Можна запропонувати учням побудувати коло і сформулювати його означення. Напевно, із першим завданням учні впораються, а з формулюванням означення виникнуть складнощі.

Отже, завдання на урок: вивчити означення кола та його елементів, навчитися використовувати ці означення для знаходження елементів кола на рисунку, зображення елементів кола та для розв’язування задач.

ІV. Актуалізація опорних знань

Виконання усних вправ

1. Довжина відрізка AB дорівнює 10 см. Яка відстань між точками A і B?

2. Дано точку O. Скільки відрізків довжиною 10 см можна відкласти від точки O:

1) на промені OA;

2) на прямій OA;

3) на площині?

3. На відрізку AB позначено точку O таку, що AO=BO. Виразіть довжину AB через AO.

V. Засвоєння знань

План вивчення нового матеріалу

1. Означення кола; властивість точок кола.

2. Означення круга; властивість точок круга.

3. Елементи кола.

4. Співвідношення між відрізками в колі.

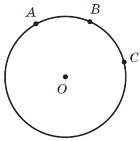
Оскільки з поняттям кола та його елементів учні ознайомлені з попередніх класів, то розпочати вивчення нового матеріалу можна з повторення, а саме: запропонувати учням за рис. 1 назвати:

1) центр кола;

2) радіуси кола;

3) хорди кола;

4) діаметри кола.

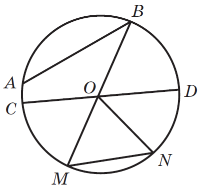
Рис. 1

Після цього вчитель сам або із залученням учнів формулює означення кола, його центра, радіуса, хорди і діаметра. При цьому необхідно звернути увагу учнів на декілька важливих моментів:

• в одному і тому самому колі можна провести безліч радіусів, діаметрів і хорд;
• усі радіуси одного і того самого кола — рівні відрізки;
• центр кола рівновіддалений від усіх його точок. Отже, якщо точка знаходиться від центра на відстані, що не дорівнює радіусу, то вона не належить колу;
• діаметр — це найбільша хорда;
• центр кола можна розглядати як точку перетину його діаметрів.

Пояснюючи новий матеріал, бажано використовувати конспект .

Коло та його елементи
1. Означення Колом називають геометричну фігуру, яка складається з усіх точок площини, рівновіддалених від даної точки. Ця точка називається   центром кола. Точки O, A, B, C належать площині, A, B, C — рівновіддалені від точки O, тому точки A, B, C належать колу з центром у точці O радіуса R=OA=OB=OC=...
2. Елементи	O — центр кола; OA=OB=OC=R — радіуси кола (точки A, B і C лежать на колі); AB — хорда (точки A, B лежать на колі); BC=d — діаметр (BC — хорда, що проходить через центр). BC=d=2R

Радіусом називається відрізок, який сполучає будь-яку точку кола з його центром.

Хордою називається відрізок, який сполучає будь-які дві точки кола.

Діаметром називається хорда, що проходить через центр кола.

Будь-які дві точки поділяють його на частини, які називаються дугами.

VІ. Формування вмінь

Виконання усних вправ

1. Радіус кола дорівнює 9 см. Чому дорівнює діаметр цього кола?

2. Діаметр кола дорівнює 17 см. Чому дорівнює радіус?

3. На рис. 1 ∠MON =70°. Знайдіть решту кутів трикутника MON.

4. У колі з центром O проведена хорда AB, що дорівнює радіусу кола. Обчисліть кути трикутника AOB.

5. Коло з центром у точці O має радіус 10 см. Де знаходиться точка M, якщо:

1) OM<10 см; 2) OM=10 см; 3) OM>10 см?

Виконання письмових вправ

1. Побудуйте коло з центром O радіусом 3 см.

1) Проведіть у цьому колі радіус, діаметр і хорду, яка не є діаметром. Який із цих відрізків не проходить через центр кола?

2) Виділіть на рисунку відрізок, довжина якого дорівнює 6 см.

3) Позначте всередині кола точку, яка не збігається з точкою O. Скільки радіусів, діаметрів, хорд можна провести через позначену точку?

2. Знайдіть діаметр кола, якщо він на 8 см більший, ніж радіус цього кола.

3. Відрізки AC і BD — діаметри кола з центром O.

1) Доведіть рівність трикутників AOB і COD.

2) Знайдіть периметр трикутника COD, якщо

AC=14 см, AB=8 см.

4. З однієї точки кола проведено діаметр і хорду, яка дорівнює радіусу кола. Знайдіть кут між ними.

5. На рис. 2 відрізки AB і CD — рівні хорди кола з центром O. Доведіть рівність кутів AOC і BOD.

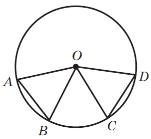
Рис. 2

Робота з підручником Геоматрія 7 клас Бурда М.І., Тарасенкова Н.А., 2015 р.

§17, №588, №592, №594, №595, №605.

VІІ. Підсумки уроку

Виконання усних вправ

1. Наводячи приклади хорд, учень сказав: «Прикладами хорд кола є діаметри і радіуси». Чи правильно це?

2. Чи може хорда бути втричі більшою за радіус того ж самого кола?

3. На колі позначено точку. Скільки діаметрів і скільки хорд можна провести через цю точку?

4. Продовжимо всі радіуси кола на одну й ту саму довжину (у бік, протилежний до центра). Яку лінію утворять їх кінці? Відповідь поясніть.

VІІІ. Домашнє завдання

Повторити теоретичний матеріал за відповідним параграфом підручника.

Дати відповіді на запитання:

1. Дано коло радіуса R із центром O і точку A. Порівняйте R із довжиною відрізка OA, якщо точка A:

1) лежить на цьому колі;

2) лежить усередині круга, обмеженого поданим колом;

3) не належить кругу, обмеженому поданим колом.

2. Скільки спільних точок із колом має:

1) промінь, початком якого є центр кола;

2) пряма, що проходить через центр кола?

3. Точка перетину двох діаметрів кола сполучена з точкою кола. Яку довжину має отриманий відрізок, якщо діаметр кола дорівнює d?

4. Дві хорди кола мають спільний кінець. Чи можуть обидві вони бути діаметрами?

Розв’язати задачі.

1. Діаметр кола дорівнює 11 см. Знайдіть радіус кола.

2. Відрізки OA і OB — радіуси кола з центром O, причому

∠AOB =60°.

Знайдіть периметр трикутника AOB, якщо

AB=5 см.

3. O — центр кола (рис. 1). Доведіть, що AD||BC, AD=BC.

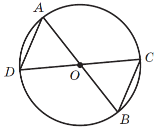
Рис. 1

Підручник: №593, №596, №603