Урок з геометрії для учнів 11-го класу з професійним спрямуванням, рівень стандарт "Площа бічної та повної поверхні конуса"

 

Білозерський професійний гірничий ліцей

 

 

 

 

 

 

 

 

 

 

Методична розробка уроку

«Площа бічної та повної поверхні конуса»

 

 

 

 

Розробив викладач:

Суббота Олена Олександрівна

 

 

 

 

 

 

м. Білозерське 2018

Зміст

 

1. Вступ    3
2. Основна частина   4
3. Використані джерела  12
4. Додатки  13

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Вступ

 

Однією з проблем, з якою зустрічаються викладачі професійно-технічних навчальних закладів, є відсутність інтересу учнів до навчання, зокрема до вивчення геометрії. Завдання викладача полягає в тому, щоб зацікавити учня, прищепити йому інтерес до вивчення предмету. Одним із дієвих засобів зацікавлення учнів математикою, зокрема геометрією, є проведення уроків з використанням елементів з професійним спрямуванням. Такі уроки вимагають від викладача спеціальної підготовки, але дають можливість показати тісний зв’язок математики з обраною професією.

Урок засвоєння нових знань і вмінь з теми «Площа бічної та повної поверхні конуса» розроблений для учнів 3 курсу з професії «Слюсар із складання металоконструкцій; електрогазозварник», які навчаються за підручником Г.П. Бевз, В.Г. Бевз «Математика» 11 клас. Рівень стандарту, та  спрямований на формування професійних компетенцій учнів.

Під час підготовки до уроку мною було залучено групу учнів до творчої співпраці. З метою повторення теоретичного матеріалу для подальшого застосування при вивченні нової теми їм було запропоновано творче завдання – виготовити модель конуса та розробити презентацію з теми «Конус».

Поняття площі поверхні вводиться з опорою на просторове уявлення учнів, а потім формується строге визначення. Практична направленість уроку визначається значною кількістю задач з професійним спрямуванням.

На даному уроці мною використовуються різні методи і форми інтерактивного навчання та самостійної роботи учнів. Використання новітніх технологій дозволяє проводити пояснення нового матеріалу за допомогою мультимедійного проектора. Застосування презентацій майже на всіх етапах уроку дозволяє зробити урок більш насиченим і продуктивним, активізувати пізнавальну діяльність учнів, підвищити наочність навчального матеріалу, моделювати геометричні об'єкти, скоротити час на побудову креслень до задач. Використання задач за готовими рисунками також заощаджує багато часу.

Під час уроку учням пропонується інтерактивна вправа «Мозковий штурм». Це змушує їх аналізувати, порівнювати, спостерігати, узагальнювати, робити висновки. Запропоновані на уроці задачі не є типовими, які розв'язуються за зразком. Це сприяє активізації розумової діяльності учнів.

 

Площа поверхні конуса

Тема: Геометричні тіла. Об’єми та площі поверхонь геометричних тіл.

Тема уроку: Площа бічної та повної поверхні конуса.

Мета уроку: навчальна: сформувати поняття площі бічної та повної поверхні конуса; ознайомити учнів із формулами для знаходження площ бічної та повної поверхні конуса, зрізаного конуса; сформувати вміння застосовувати набуті знання на практиці;

розвиваюча: розвивати просторове уявлення, логічне мислення, пам'ять, вміння аналізувати та вільно висловлювати свої думки, розширювати світогляд учнів;

виховна: виховувати графічну культуру, старанність, інтерес до вивчення математики.

Тип уроку: урок засвоєння нових знань і вмінь.

Міжпредметні зв’язки: фізика, технічне креслення, спецтехнологія складання металевих конструкцій, виробниче навчання.

Методи навчання: інтерактивні, проблемно-пошукові, практичні, словесні, наочні.

Обладнання і наочність: модель конуса, розгортка конуса, мультимедійна презентація «Конус», «Площа поверхні конуса», мультимедійний проектор, роздатковий матеріал, опорна схема «Конус»

План уроку:

 

№ з\п	Назва етапу уроку	Час, хв.	Методи та прийоми
1.	Організаційний момент	1	Ігрова розминка
2.	Перевірка домашнього завдання	2	Самоперевірка
3.	Актуалізація опорних знань і вмінь	10	Мультимедійна презентація
4.	Мотивація навчальної діяльності	2	Звернення до класу Створення проблемної ситуації
5.	Вивчення нового матеріалу	15	Пояснення викладача Мультимедійна презентація
6.	Засвоєння нових знань і вмінь	12	«Мозковий штурм»
7.	Підсумок уроку	2	Технологія «Мікрофон»
8.	Домашнє завдання	1

Хід уроку

 

І. Організаційний етап

• Перевірка обліку учнів.
• Повідомлення теми та мети уроку. (Додаток  Д, слайд 1,2)
• Ігрова розминка «Мій настрій»

(Додаток  Д, слайд 3)

Щоб налаштувати учнів на успішну роботу, створити сприятливу психологічну атмосферу та оцінити готовність до роботи, викладач пропонує учням передати свій настрій оплесками: гарний настрій – це гучні оплески, поганий – слабкі.

 

ІІ. Перевірка домашнього завдання

• Самоперевірка

Перевірку правильності виконання домашнього завдання викладач проводить по записам на дошці, зробленим до початку уроку. Учні усно коментують хід розв’язування задач.

ІІІ. Актуалізація опорних знань і вмінь

Для вивчення нової теми треба повторити відомості про конус. Це ми можемо зробити за допомогою мультимедійної презентації, яку підготували ваші одногрупники

1. Перегляд мультимедійної презентації «Конус» ( Додаток А)
2. Математичний диктант ( Додаток Б)
3. Робота в парах

Розв’язування задач на знаходження елементів конуса за готовими рисунками

• Учні, які сидять разом за однією партою отримують картки із завданнями ( Додаток В) і опорні схеми з теоретичним матеріалом ( Додаток Г)
• Два учня розв’язують дані задачі на закритих дошках (для подальшої перевірки)

 

ІV. Мотивація навчальної діяльності

У вашій професії без математики не обійтися. На уроках спецтехнології та виробничого навчання вам часто доводиться вирішувати математичні завдання.

Створюється проблемна ситуація. (Нагадуємо що таке пожежний щит)

(Додаток  Д, слайд 5)

Задача. 

Цех металоконструкцій ПАО «НКМЗ» отримав заказ на виготовлення конусних відер діаметром 28см і висотою 39см для оформлення пожежних щитів. У наявності є листи заліза розміром  2 м × 1,5 м. Скільки можна виготовити конусних відер з одного такого листа заліза ?

Відповідь можна дати дуже швидко, якщо знати формулу, з якою ви ознайомитеся на уроці.

Учні записують тему уроку

V. Вивчення нового матеріалу викладач проводить за допомогою комп’ютерної презентації. (Додаток  Д )

Бічну поверхню конуса, як і бічну поверхню циліндра, можна розгорнути на площину, розрізавши її по твірній. (Демонструється геометрична фігура конуса)

(Додаток  Д, слайд 6-7)

            

 

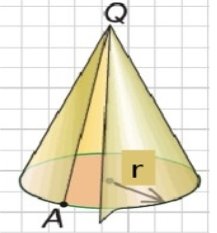
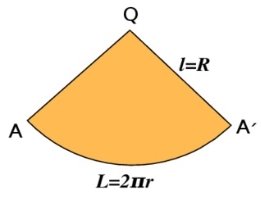
Рисунок 1. Розгортка бічної поверхні конуса

Що є розгорткою бічної поверхні конуса? (Круговий сектор, демонструється модель розгортки бічної поверхні  конуса)

Розгорткою бічної поверхні конуса є круговий сектор. Його радіус дорівнює твірній конуса, а довжина дуги сектора дорівнює довжині кола  основи конуса. Площею бічної поверхні конуса будемо вважати площу її розгортки.

(Додаток  Д, слайд 8)

Виразимо площу бічної поверхні конуса S_б.п. через його твірну ℓ і радіус основи R.

      Площа бічної поверхні конуса дорівнює добутку половини довжини кола основи на твірну.

Якщо довжина кола основи дорівнює: С = 2πR, то

S_б.п. = πRℓ

Основою конуса є круг, тому площа основи конуса дорівнює:

S_осн. = πR²

(Додаток  Д, слайд 9)

     Площею повної поверхні конуса називається сума площ бічної

поверхні й основи конуса. Для обчислення площі повної поверхні конуса S_к одержуємо формулу:      S_п.п. = S_б.п.+ S_осн 

S_п.п. = πRℓ + πR²

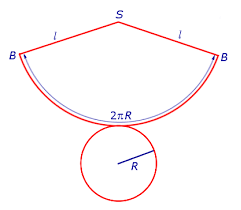
Рисунок 2. Розгортка повної поверхні конуса

(Додаток  Д, слайд 10)

     Площа поверхні зрізаного конуса:

S_б.п. = πℓ(R + r)

S_п.п. = πℓ(R + r) + πR² + πr ²

де R і r – радіуси основ зрізаного конуса, ℓ - твірна зрізаного конуса

 

(Додаток  Д, слайд 11)

Повертаємося до практичної задачі, розглянутої на початку уроку, яка зводиться до знаходження площі бічної поверхні конуса.

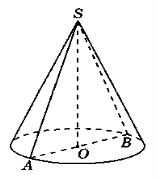Розв’язання:

 

 

 

 

 

 

АВ = d = 28 см, отже ОА = R = 14 см,  SO = H = 39 см.

Із трикутника SOA ( SOA = 90°) отримаємо за теоремою Піфагора:

ℓ = SA =

ℓ = =

Відомо, що тоді 

Площу листа можна обчислити за формулою площі прямокутника:

S_листа =  отже

S_листа = 200 · 150 = 30000 см².

 

Який висновок ми зможемо зробити? Скільки можна зробити відер?

       Відповідь: 16 відер.

IV. Засвоєння нових знань і вмінь

• Розвязування задач усно (Додаток  Д, слайд 12)

Обчисліть площу бічної поверхні конуса

• Розвязування задачі практичного змісту

Інтерактивна вправа «Мозковий штурм»

Цей прийом полягає у колективній творчій роботі з розв’язання певної складної проблеми. Всіх учнів об’єднує спільна робота над пошуком істини.

Після презентації умови задачі, яку необхідно розв’язати (умова задачі записана на мультимедійному екрані) викладач пропонує всім висловити ідеї, коментарі, шляхи розв’язання. Усі пропозиції записуються на дошці в порядку їх оголошення без зауважень, коментарів чи запитань. Необхідно заохочувати всіх до висування якомога більшої кількості ідей. У класі можна повісити плакат, або оформити слайд презентації.

(Додаток  Д, слайд 13-14)

 

 

 

 

 

На закінчення обговорюються й оцінюються запропоновані ідеї. Учень біля дошки виконує скорочений запис задачі, розв’язує її.

 

Задача.

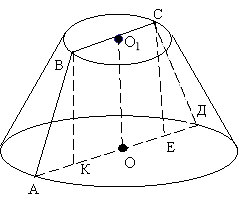
До витяжної труби над котлом потрібно приладнати ковпак у формі зрізаного конуса, розміри якого (у метрах) надані на кресленні (Рисунок 3.) Скільки квадратних метрів листового заліза потрібно для його виготовлення? (Обрізки не беруться до уваги.)

                                   

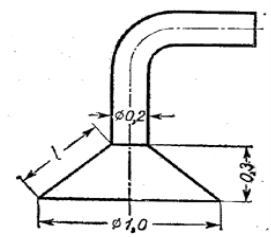
Рисунок 3. Витяжна труба

Розв’язання:

 

 

 

 

ВС = D₁ = 20 см, отже ВО₁ = R₁ = 10 см,

АД = D₂ = 100 см, отже АО = R₂ = 50 см,  H = ОО₁ = 30 см.

АВО₁О – трапеція (за означенням)

Із прямокутника КВО₁О:  ВО₁ = КО = 10см,  ВК = О₁О = 30см,

АК = 50 – 10 = 40 см.

Із трикутника AВК ( АКВ = 90°) отримаємо за теоремою Піфагора:

ℓ = AВ =

ℓ = =

Відомо, що   тоді

9420см² = 0,942м² 1м²

Який висновок ми можемо зробити? Скільки квадратних метрів листового

заліза потрібно для виготовлення ковпака?

       Відповідь: 1м².

 

V. Підсумок уроку. Оцінювання учнів.

Підсумок уроку викладач проводить за технологією «Мікрофон»

Викладач ставить запитання до учнів. Учням запропоновано певний предмет, що виконуватиме роль мікрофона. Діти передають його один одному, по черзі беручи слово. Відповідає тільки той, у кого є уявний мікрофон.

(Додаток  Д, слайд 15-16)

Питання до учнів:

1. Який з рисунків є розгорткою конуса?
2. З чого складається бічна поверхня конуса? Як позначається?
3. За якою формулою можна обчислити бічну поверхню конуса?
4. З чого складається повна поверхня конуса? Як позначається?
5. За якою формулою можна обчислити повну поверхню конуса?
6. За якою формулою можна обчислити бічну поверхню зрізаного конуса?
7. За якою формулою можна обчислити повну поверхню зрізаного конуса?

 

(Додаток  Д, слайд 17-18)

VІ. Домашнє завдання

Розділ 6, §32, контрольні питання (ст.246); вивчити формули; задача № 1043.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Використані джерела:

1. Бевз Г.П., Бевз В.Г.  Математика: 11 кл. : підручник для загальноосвітніх навч. Закл.: рівень стандарту. – К.: Генеза, 2011. – 320с.
2. Інтерактивні технології на уроках математики / Уклад. І.С.Маркова. Х.: Вид.група «Основа», 2008. – 126с.
3. Корнієнко Т.Л. Математика: 11 кл. Рівень стандарту: Розробки уроків. – Х.: Видавництво «Ранок», 2012. – 368с.
4. Роганин А.Н., Геометрия. 11 класс: Планы-конспекты уроков. – Харьков: Веста: Издательство «Ранок», 2004. – 256с.
5. Рыбкин Н. Сборник задач по геометрии. Часть ІІ. Стереометрия. 9 – 10 класс средней школы. – М.: Гос. Учебно-педагогическое издательство министерства просвещения, 1961. – 88с.
6. Сухарева  Л.С. Завдання для усної роботи, математичні диктанти та тести. Геометрія. 10-11 кл. – Х.: Вид.група «Основа», 2008. – 126с.
7. П’ятницька Н.В. Площі поверхонь тіл обертання. Урок геометрії в 11 класі.  Журнал «Математика в школах України» № 3 (447) – Січень 2015
8. Картинки с сайта  https://images.google.com/

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ДОДАТОК   Б

 

Тест на встановлення відповідностей

Зіставте формули з відповідними поняттями

1	V = πR2·H	А	Довжина кола
2	c2 = a2 + b2	Б	Радіус круга
3	C = 2πR	В	Площа круга
4	d = 2R	Г	Теорема Піфагора
5	S = πR2	Д	Об’єм конуса
6	R = d	Е	Діаметр круга

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ДОДАТОК   В

КАРТКА №1

Самостійна робота

Тема: «Конус»

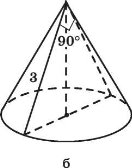
За готовими рисунками знайдіть елементи конуса.

 

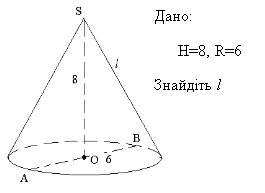
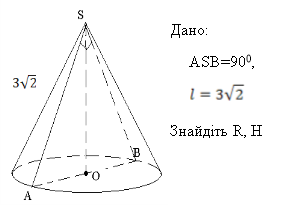1.

 

 

 

 

 

 

 

 

КАРТКА №2

Самостійна робота

Тема: «Конус»

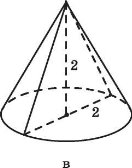
За готовими рисунками знайдіть елементи конуса.

 

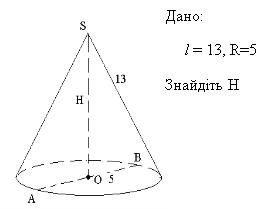
1.

 

 

 

 

 

 

ДОДАТОК   Г

Конус 

 

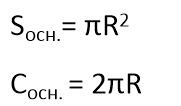
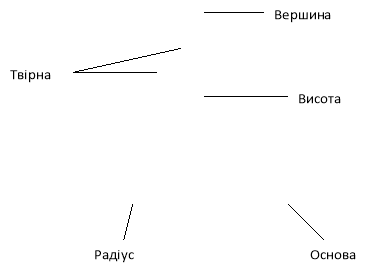
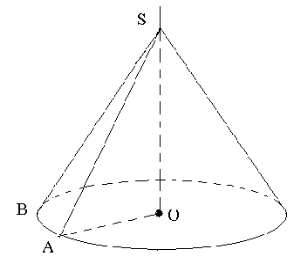
Переріз конуса площинами

 

 

 

 

 

 

 

 

 

 

 

 

 

 

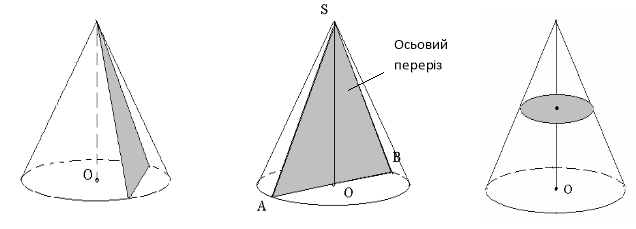
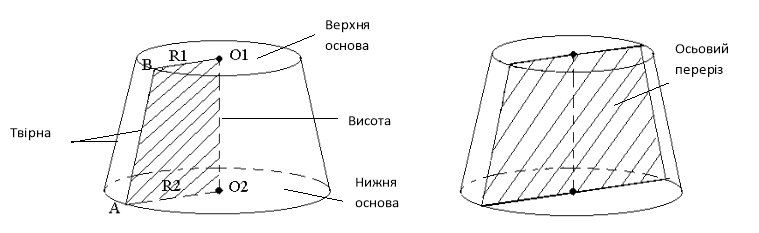Зрізаний конус