Урок з геометрії для учнів 11 класу на тему "Правильні многогранники"

УРОК НА ТЕМУ: «ПРАВИЛЬНІ МНОГОГРАННИКИ»

 

Бокало Г.В., викладач математики ВПУ №29 м.Львова

 

 Тема уроку: Правильні многогранники.

 Мета уроку:

Навчальна: Формувати поняття правильного многогранника, розглянути кожен з п’яти видів правильних многогранників, вдосконалювати навички розв’язування задач.

Розвиваюча: Розвивати творчу активність учнів, просторову уяву, пам’ять, розвивати логічне мислення, уміння аналізувати.

Виховна: Виховувати свідоме ставлення до навчання, цілеспрямованість, працелюбність, виховувати культуру праці.

Тип уроку: комбінований.

Методи проведення уроку: робота в групах, бесіда, розповідь.

Міжпредметні зв’язки: Біологія, історія, хімія, архітектура, художня культура.

Обладнання: Комп’ютер, мультимедійна презентація, моделі правильних многогранників, роздатковий матеріал.

Література:

1. Г. П. Бевз, В. Г. Бевз. Математика: 11 кл.: підруч. для загальноосвіт. навч. закл.: рівень стандарту. -  К.: Генеза, 2011р.
2. Т. Л. Корнієнко, В. І. Фіготіна. Математика. 11 клас. Академічний рівень: Розробки уроків. – Х: Видавництво «Ранок», 2014 р.
3. О. М. Роганін. Геометрія. 11 клас: Плани-конспекти уроків.- Х., 2010р.
4. О. О. Старова. Геометрія. 11 клас, рівень стандарту. - Х., 2017 р.
5. Інтернет джерела: https://uk.wikipedia.org/wiki/

Епіграф уроку:

Правильних многогранників надзвичайно мало, але цей дуже скромний за кількістю загін зумів пробитися у найбільші глибини різних наук.

Льюїс Керрол

Хід уроку

I. Організаційний момент

Привітання, перевірка присутності учнів, готовності їх до уроку.

“Від того настрою, з яким ви вступаєте в день, або в якусь справу, залежать ваші успіхи, а можливо, і невдачі”. Конфуцій

 Я бажаю вам розпочати урок з гарним настроєм і отримати від нього задоволення і гарні результати.

 

II. Актуалізація опорних знань учнів

“Як приємно дізнатися, що ти чогось навчився”                                       Мольєр

На домашнє завдання вам було повторити все про призми та піраміди. А оскільки ви поділені на дві команди, то кожна команда вибере питання, на які буде відповідати.

На столі лежать 2 набори питань, учасник від кожної команди вибирає один з них. Кожній команді дається 3-4 хв на відповіді. Закінчується час, зупиняються відповіді.

 

Набори питань для команд:

1-ій набір питань:

Означення призми. Правильна призма це… Пряма призма це … Який многокутник може лежати в основі призми? Поверхня призми складається … Бічна поверхня призми складається … Властивості основ призми. Які між собою бічні ребра прямої призми?

 

2-ий набір питань:

Означення піраміди. Правильна піраміда це… Пряма піраміда це … Поверхня піраміди складається … Який многокутник може лежати в основі піраміди? Бічна поверхня піраміди складається … Висотою піраміди називається … Яка піраміда називається n-кутною?

 

III. Мотивація навчальної діяльності

Геометрія являє собою могутній інструмент пізнання світу.

Тема сьогоднішнього уроку “Правильні многогранники”.

Існує всього 5 правильних багатогранників. Назва кожного правильного многогранника походить від грецької назви кількості його граней і слова “грань”. Правильні многогранники мають багату історію, яка пов’язана з таким знаменитими ученими старовини, як Піфагор, Платон, Евклід, Архімед, Кеплер.

 

 

Піфагор	Платон		Евклід
Архімед		Кеплер

 

В античній філософії першоосновою буття вважали 4 стихії: вогонь, земля, повітря і вода. Древньогрецький філософ Платон надавав атомам цих “стихій” форму тетраедра, куба, октаедра та ікосаедра. Форму додекаедра Платон надавав усьому Всесвіту.

Жодне геометричне тіло не має такої довершеності та краси, як правильні многогранники. Сьогодні на уроці ми ознайомимося з поняттям правильних многогранників, їх видами та елементами. Знайдемо правильні многогранники у природі, історії, архітектурі, мистецтві.

 

IV. Сприймання й усвідомлення нового навчального матеріалу

Означення: Правильним називається опуклий многогранник, у якого всі грані – рівні правильні многокутники й у кожній вершині сходиться однакове число ребер.

Оскільки існує п’ять видів правильних многогранників і кожен з них має певну кількість граней, вершин, ребер, то я вам роздаю таблички, які ви будете заповнювати протягом пояснення.

 

Назва	К-сть граней (Г)	К-сть вершин (В)	К-сть ребер (Р)	К-сть вершин і граней (Г + В)
Тетраедр
Куб
Октаедр
Ікосаедр
Додекаедр

 

Види правильних опуклих многогранників: правильний тетраедр, куб, октаедр, додекаедр, ікосаедр.

 

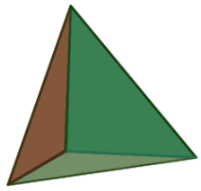
1. Правильний тетраедр

Означення: Правильним тетраедром називається многогранник, у якого всі грані правильні трикутники і в кожній вершині сходиться по 3 ребра. Тетраедр має такі елементи: Вершин – 4 Ребер – 6 Граней – 4 Висота тетраедра – довжина перпендикуляра опущеного з вершини на площину.

 

У фізичному світі тетраедр зустрічається у:

крижаних кристалах

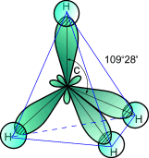
молекулах метану

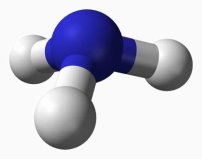
молекулах аміаку

 

Тетраедр в архітектурі:

У Новому Орлеані розроблено “Будівлю місто”, висота якої 365 метрів, вона включає в себе 20 000 квартир, загальна площа 2 040 000 м кв. Будівля використовує екологічні енергоносії – енергію вітру, води і сонця. Крім квартир, в тетраедрі розташовані комерційні організації, 3 готелі, культурні об’єкти, школа, лікарня.

Враховуючи місце, під яке створювався проект, його дуже важлива особливість – здатність триматися на плаву.

 

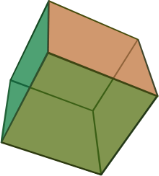
2. Куб або гексаедр

Означення: Правильним гексаедром називається многогранник у якого всі грані – квадрати і в кожній вершині сходиться по 3 ребра. Куб має такі елементи: Вершин – 8 Ребер – 12 Граней – 6 Висота гексаедра – це довжина ребра.

Куб в архітектурі:

Архітектура в Ніцці -  “Кубічна Голова”.

 

От що буває від великого розуму. Хоча, голова корисна – оскільки в ній розміщена адміністрація міської бібліотеки.

 

У фізичному світі куб зустрічається у:

кристалах кухарської солі,

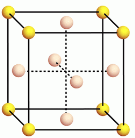
кристалічних решітках таких металів:

алюміній,

 золото, срібло, залізо, цинк.

 

За образним виразом Піфагора “сіль була народжена найшляхетнішими батьками – сонцем і морем”.

Україна має великі та унікальні за якістю поклади сировини для кухонної солі, за хімічною чистотою їх можна вважати найкращими у світі. Основні запаси: Прикарпаття, Донбас, Закарпаття, а також у Криму. Високоякісні кам’яні солі є важливою складовою експорту України. Тисячоліття тому сіль була настільки дорогою, що через неї влаштовували війни. Зараз сіль є найдешевшою з усіх видів харчових добавок.

 

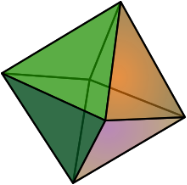
3. Октаедр

Означення:Правильним октаедром називається многогранник, у якого всі грані – правильні трикутники і в кожній вершині сходиться 4 ребра.  Октаедр має такі елементи: Вершин – 6 Ребер – 12 Граней – 8

 У формі октаедра кристалізуються

мідь

алмаз

срібло

 

Алмаз – це дорогоцінний кристал і є найтвердішим з речовин. У промислові алмази, завдяки їх надзвичайній твердості, використовують для шліфування, свердління і різання, буріння твердих гірських порід, обробки твердих металів та інших сплавів тощо.

Огранені ювелірні алмази називають діамантами. За останніми дослідженнями в Україні виявлені дві перспективні ділянки щодо знаходження алмазоносних кімберлітів, які розташовані на Донеччині і Рівненщині.

 

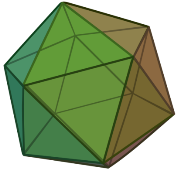
4. Ікосаедр Означення: Правильним ікосаедром називається многогранник, у якого всі грані – правильні трикутники і в кожній вершині сходиться 5 ребер.  Ікосаедр має такі елементи: Вершин - 12 Ребер – 30 Граней – 20

 

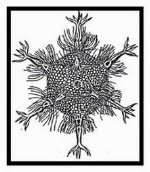
Більшість феодарій живуть на морській глибині і служать здобиччю коралових рибок. Але проста тварина намагається себе захистити: з 12 вершин

виходять 12 порожнистих голок. На кінцях знаходяться зубці, що роблять голку ефективною при захисті. З усіх многогранників з такою ж кількістю граней саме ікосаедр має найбільший об’єм і найменшу площу. Ця властивість дозволяє морському організму долати тиск води.
	Феодарії
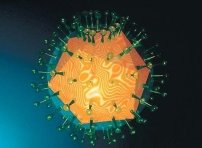
Вірус герпесу		Винятковістю ікосаедра скористалися віруси. Вірус не може бути абсолютно круглим, як вважалося раніше. Вірус у формі ікосаедра досягає максимальної економії генетичної інформації.

 

5. Додекаедр

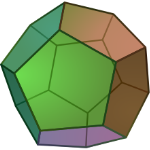
Означення: Правильним додекаедром називається многогранник, у якого всі грані – правильні п’ятикутники і в кожній вершині сходиться 3 ребра. Додекаедр має такі елементи: Вершин – 20 Ребер – 30 Граней – 12

 

Деякі з правильних тіл зустрічаються у вигляді кристалів, інші у вигляді вірусів, чи найпростіших мікроорганізмів.

Вірус поліомієліту має форму додекаедра. Він може жити і розмножуватися тільки в клітинах людини і приматів. Заразитись поліомієлітом можна тільки від людей. Віруси передаються через переносників (кліщі).

Додекаедр та ікосаедр є параметрами ДНК, по якій побудоване усе життя.

Молекули ДНК є кубом, що обертається. При повороті куба на 72 градуси  виходить ікосаедр, який складає пару додекаедру.

Молекула ДНК

Кристал піриту – природна модель додекаедра.

 

На картині Сальвадор Далі “Таємна Вечеря”, Ісус Христос і 12 Його учнів знаходяться у модерністському інтер’єрі зі скляними стінами. Апостоли, нахиливши голови, стоять на колінах навколо стола. Сальвадор Далі створив цю картину за математичними принципами. Відчувається вплив Леонардо да Вінчі: всесвіт – це додекаедр.

 

Сальвадор Далі “Таємна Вечеря”

 

V. Осмислення, узагальнення і систематизація знань

Назва	К-сть граней (Г)	К-сть вершин (В)	К-сть ребер (Р)	К-сть вершин і граней (Г + В)
Тетраедр	4	4	6	8
Куб	6	8	12	14
Октаедр	8	6	12	14
Ікосаедр	20	12	30	32
Додекаедр	12	20	30	32

 

Евристична бесіда:

•    Чи не помічаєте ви якоїсь закономірності?
•    Запишемо її так: Г + В = Р + 2.

Так ми отримали формулу, яка була відкрита швейцарським математиком Леонардом Ейлером у 1752 році.

Це теорема про співвідношення між числами граней, ребер і вершин.

 

Запитання до учнів:

• Який многогранник називається правильним?
• Скільки існує видів правильних многогранників?
• Чи існує піраміда, яка є правильним многогранником?
• Чи існує призма, яка є правильним многогранником?

 

Розв’язування задач:

1. У тетраедра площа однієї грані 4 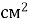. Знайти площу всього тетраедра.
2. Скільки потрібно дроту, щоб виготовити куб, ребро якого дорівнює 20 см?
3. Знайти периметр однієї грані октаедра, якщо його ребро дорівнює 5 см?
4. Площа однієї грані гексаедра дорівнює 144 см². Знайдіть діагональ цього многогранника.

 

VI. Підсумок уроку

Правильні многогранники існували на землі задовго до появи на ній людини. Але тільки геометри побачили в них порядок і систему задовго до того, як фізики проникли в таємницю будови речовини.

Судячи з цього правильні многогранники будуть відігравати все важливішу роль у різних галузях знань, адже ці фігури внутрішньо зв’язані з природними явищами.

Як говорив Платон, із усіх відомих тіл вони найпрекрасніші, при чому кожен многогранник прекрасний по-своєму. Мабуть, це той випадок, коли краса та істина – єдине ціле.

 

VIІ. Домашнє завдання

Г. П. Бевз, В. Г. Бевз. Математика: 11 кл.: підруч. для загальноосвіт. навч. закл.: рівень стандарту. -  К.: Генеза, 2011р.

§ 30 ст. 230-236, № 976, 978, 980.