«Метод координат на плоскости и в пространстве»

 

 

ПОДГОТОВКА и КОНСПЕКТ

 

 

интегрированного комбинированного урока

(математика-информатика)

в 9 и 11 классах

 

 

«Метод координат на плоскости и в пространстве»

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Учитель  Щербань Татьяна Ивановна

 

 

Предмет: математика – информатика

 

Тема: «Метод проектов на плоскости и в пространстве»

 

Продолжительность: 2 урока по 45 минут

 

 

Технологии:

 

Факторы, которые необходимо учитывать при проектировании уроков с использованием ИКТ:

Во-первых, проводится детальный анализ ресурсов с позиций принципа генерализации информации, прогнозируется эффективность использования данного ресурса при проведении различного рода занятий, определяется методика их проведения и проектируются основные виды деятельности с данными ресурсами в учебном процессе.

Приветствие. Проверка наличия обучающихся. Подготовка к работе.

 

1. Мотивация учения школьников и сообщение темы и цели урока

Почему мы проводим такой урок? Уже вторую четверть обучающиеся 9-х и 11-х классов на уроках геометрии изучают одну тему. И мы решили воспользоваться представившейся возможностью показать вам, что изучение математики в школе основано наряду с другими принципами (научность, доступность, наглядность и т.д.) на принципе концентризма. Если изобразить уровень знаний обучающихся 9-х классов окружностью, то концентрическая окружность большего радиуса будет изображать уровень одиннадцатиклассников. Но, учитывая, что процесс обучения непрерывный, нагляднее было бы процесс познания изобразить в виде спирали.

Так как мы возвращаемся часто к тем же вопросам, что изучали раньше, но на более высоком уровне.

Мы решили не упустить и другую возможность. Раз уж собрали вас вместе, то попросили одиннадцатиклассников принять зачёт по решению задач по данной теме у девятиклассников.

Обобщая на сегодняшнем уроке метод координат, мы будем говорить о его достоинствах, универсальности, исключительности.

И, естественно, отдадим дань уважения гениальному автору этого метода.

Итак, записываем тему урока «Метод координат на плоскости и в пространстве»

 

2. Актуализация ранее полученных знаний

 

3.1. Обучающимся задаются вопросы:

• Что такое метод координат?
• Как называются числа, с помощью которых определяется положение точки?
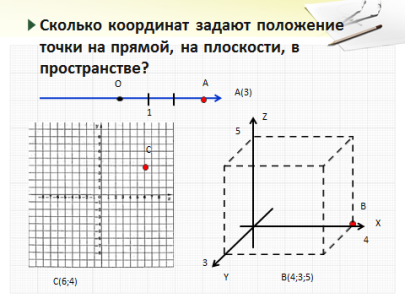
• Сколько координат задают положение точки на прямой, на плоскости, в пространстве?

 

 

Слайд № 2.

 

Слайд № 3.

 

 

 

 

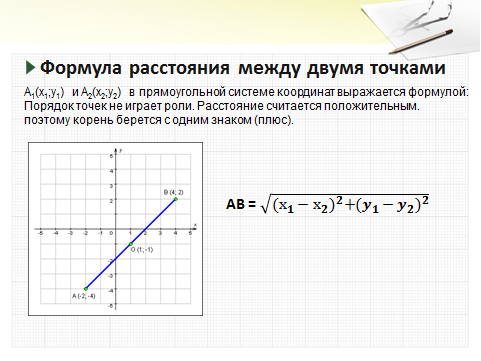
3.2. Существует небольшой набор формул, используемый при решении задач, доказательстве теорем.

 

 Слайд № 4.

 

 

 

 

Слайд № 5.

 

 

 

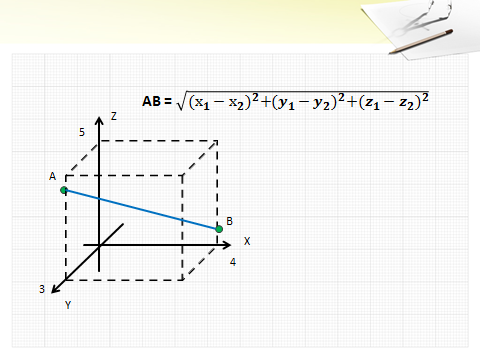
Слайд№ 6.

 

 

3. Решение задач.
   1.  Задача. Уравнения линий поверхностей.

9 класс:

• Написать уравнение окружности ((x – a)² + (y – b)² = r², где  (a;b) – центр окружности, r – радиус).
• Что задаёт уравнение x² +y² = 1 на плоскости? (окружность).
• Написать уравнение прямой в общем виде и уравнение прямой, проходящей через точки A(x₁,y₁) и B(x₂,y₂). (ax + by + c = 0,  (x – x₁)/(x₁ – x₂) = (y – y₁)/(y₁ – y₂)).

 

11 класс:

• Написать уравнение сферы ((x – x₀)² + (y – y₀)² + (z – z₀)² = r² , где (x_0; y_0; z₀) – центр сферы, r – радиус)
• Что задаёт уравнение x² +y² = 1 в пространстве? (цилиндрическую поверхность – прямой круговой цилиндр).
• Написать уравнение плоскости (ax + by + cz + d = 0)

 

 

 

 Слайд № 7.

 

 

 

2.  Задача. Задание линии или поверхности уравнением.

9 класс:

• x² + y² – 2x – 4y – 20 = 0 ((x - 1)² + (y – 2)² = 25 - окружность).

 

11 класс:

• x² + y² + z² – 2x – 4y – 27 ((x – 1)² + (y – 2)² + z² = 32 – сфера).

 

Слайд № 8.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Слайд № 9.

Динамическая пауза.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3.  Геометрические построения в САПР КОМПАС.

 

В случае затруднения выполнения задания можно воспользоваться электронным файлом помощи!

 

9 класс: Из точки М(-7;3) провести касательную к окружности x² + y² – 2x – 4y – 20 = 0.

 

 

 

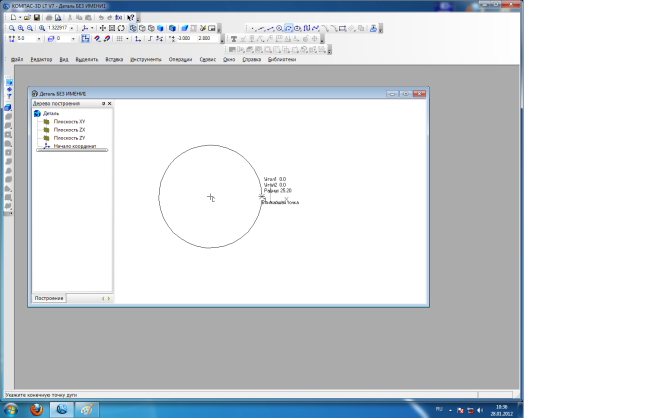
11 класс: Из точки М(-7;3;-4) провести касательную к сфере x² + y² + z² – 2x – 4y – 27 = 0.

 

Слайд № 10.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

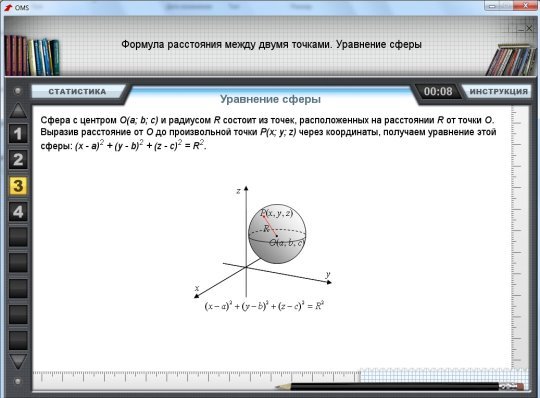
Слайд № 11.

4.  Задача. Уравнение касательной.

9 класс:

• Из точки М(-7;3) проведена касательная к окружности x² + y² – 2x – 4y – 20 = 0. Найти расстояние от точки М до точки касания.
• Сколько касательных к окружности можно провести через точку М?

 

11 класс:

• Из точки М(-7;3;-4) проведена касательная к сфере x² + y² + z² – 2x – 4y – 27 = 0. Найти расстояние от точки М до точки касания.
• Можно использовать этот чертёж в стереометрии?

 

 

УРОК II

 

1. Организационный момент.
2. Электронный тест «Декарт»
3. О достоинствах метода:

• Основная идея метода заключается в том, что геометрические объекты (точки, прямые, кривые, …) исследуются с помощью соответствующих им алгебраических объектов (уравнений, неравенств, систем уравнений, …). Таким образом, переводя геометрические понятия на язык координат, мы вместо геометрических задач рассматриваем алгебраические.

Проиллюстрируем на простом и хорошо знакомом примере этот процесс.

 

Вопрос к классу: Сколько общих точек могут иметь прямая и окружность? Ответ хорошо известен. Однако обосновать его чисто геометрическими средствами не так уж просто (особенно для случая пересечения). Использование метода координат упрощает дело, сводя его к исследованию числа решения системы. Рассмотрим частный случай: единичная окружность с центром О и прямой y = a.

 

                x² + y² = 1                   x² + a = 1                   x² = 1 – a

                y = a                             y = a                          y = a

 

                        Уравнение может иметь единственный корень, два корня и не иметь корней.

 

• Любой случай расположения прямой и окружности можно свести к частному, если выбрать подходящим образом систему координат. Возьмём центр окружности за начало координат, радиус – за единичный отрезок, а ось OY направим перпендикулярно прямой. Получим такие же уравнения.

Ещё одно достоинство метода координат: свобода выбора системы координат позволяет при решении рассматривать наиболее простые случаи.

 

С этим встретимся сейчас при доказательстве теоремы.

 

 

 

4. Доказательство теоремы.

 

Теорема: Сумма квадратов диагоналей равна сумме квадратов всех его сторон.

 

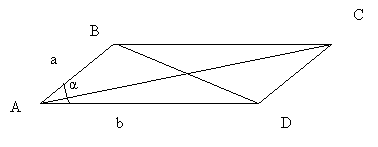
9 класс:

 

 

 

 

 

 

 

             BD² = a² + b² – 2abcosα

             AC² = a² + b² – 2abcos(180° - α) = a² + b² + 2abcosα

             BD² = a² + b² – 2abcosα + a² + b² + 2abcosα = 2a² + 2b²

 

11 класс:

 

 

 

 

 

 

 

 

AC² = (acosα + b – 0)² + (asinα – 0)² = a²cos²α + 2abcosα + b² + a²sin²α = a² + b² + 2abcosα

BD² = (acosα – b)² + (asinα – 0)² = a²cos²α – 2abcosα + b² + a²sin²α = a² + b² + 2abcosα

AC² + BD² = 2a² + 2b²

 

Какой метод понравился больше? Обучающиеся делают вывод об универсальности метода координат.

4. Выступление обучающегося с опорой на мультимедийную презентацию «Рене Декарт».

 

 

 

 

 

 

 

 

 

5. Применение метода в алгебре.

 

 

Задача. Найти наибольшее и наименьшее значение функции.

 

9 класс: f(x) = 3sinx + 4cosx

Рассмотрим векторы и {sinx;cosx}, тогда .

Известно: - || *| * ||

|

 

11 класс: f(x;y) = 6sinxcosy + 2sinxsiny + 3cosx

Рассмотрим векторы и |

|

Слайд 12.

Зрительная гимнастика.

 

6. Проверка усвоенных на уроке знаний (выходной контроль): зачёт (работа в парах – 11-классники принимают зачёт у 9-классников)
7. Подведение итогов (рефлексия). Выставление отметок по совокупности за работу на уроке.

 

Обучающиеся отправляют оценочные листы по локальной сети на сервер учителя.

Отметки выставляются в Dnevnik.ru

 

8. Сообщение домашнего задания.

Слайд № 14

 

• обязательное:

9 класс: Найти наибольшее и наименьшее значение функции

11 класс: Найти наибольшее и наименьшее значение функции

• дополнительное: Ознакомиться с другими система координат – косоугольная, координаты на окружности, полярные координаты, координаты на сфере.
• творческое: Создать мультимедийную презентацию об использовании формулы расстояния в науке и технике.
• опережающее: Вывести формулу расстояния между двумя точками в косоугольной системе координат.