Урок з геометрії на тему: «ТЕОРЕМА ПІФАГОРА», 8 клас
Розглянути різні способи доведення теореми Піфагора та вивчити біографію давньогрецького вченого, розвивати пізнавальний інтерес та інтерес до наукового пошуку.
тема: Теорема ПІФАГОР А
мета: розглянути різні способи доведення теореми Піфагора та вивчити біографію давньогрецького вченого, розвивати пізнавальний інтерес та інтерес до наукового пошуку
тип уроку: УРОК-СЕМІНАР З ЕЛЕМЕНТАМИ НАУКОВОГО ПОШУКУ
обладнання: плакати з малюнками до теорем.
словник незнайомих термінів: Рівновеликі фігури - фігури, які мають однакові площі;
План і хід уроку
І. Організаційний момент
ІІ. Піфагор. Сторінки життя
(Вступне слово вчителя)
Сьогоднішній урок ми присвятимо теоремі Піфагора. І сама теорема, і давньогрецький філософ Піфагор займають особливу нішу в історії математики. Важко знайти людину, яка б не знала знамениту теорему Піфагора. Навіть ті, хто в своєму житті після школи назавжди розпрощався з математикою, зберігають у своїй пам'яті цю теорему.
Про життя Піфагора майже не збереглося відомостей. Є підстави вважати, що він народився близько 580 - 500 р. до н.е. на острові Самос.
У молоді роки Піфагор виїхав до Єгипту вивчати науки і пробув там майже 22 роки. Під час завоювання Єгипту Персією, його захопили в полон і вивезли до Вавилону, де він прожив близько 12 років. У Вавилоні Піфагор вивчав, крім математики, астрологію й астрономію.
Здобувши широкі знання в галузі природничих наук ( у тому числі й математичних), Піфагор повернувся на о.Самос, де мав намір створити свою школу. Але в своєму рідному місті Піфагор не знайшов однодумців і переселився до м. Кротона, де організував гурток, який пізніше дістав назву Піфагорійської школи. Організація піфагорійців була таємною, одночасно і філософською школою, і політичною партією, і релігійним братством.
Наукові, насамперед математичні, дослідження Піфагора і його школи були органічно пов'язані з філософією. Так, числам натурального ряду вони надавали надприродного, містичного значення, тому математика в їх філософському трактуванні мала таємничий характер, недоступний, на їх думку, для звичайних людей.
Піфагор першим з грецьких математиків того часу знайшов пропорції і найпростіші прогресії.
Піфагорійці розрізняли три види пропорцій: арифметичну, геометричну і гармонічну.
Учні в школі Піфагора розрізняли такі види чисел: числа добрі - непарні числа, числа злі - парні числа, числа досконалі, що дорівнюють сумі своїх дільників ( наприклад, 6=1+2+3), числа дружні - такі, з яких кожне дорівнює сумі дільників другого, але без самого числа.
Можна припустити, що найпростіший з трикутників, так званий єгипетський, зі сторонами 3, 4, 5 став відомим Піфагору після подорожі країнами Сходу. (Єгипет, Вавилон). Вважають, що Піфагор знайшов доведення теореми для знаходження сторін такого трикутника, яке можна подати формулою
х ![]() + у
+ у![]() =z
=z![]()
Відкриття цієї теореми, яку історики приписують самому Піфагору, мало вирішальний вплив на подальший розвиток античної математики, бо привело встановлення існування несумісних відрізків у геометрії та ірраціональних чисел в алгебрі.
Піфагорійці знали, що сума внутрішніх кутів трикутника дорівнює 180°, що на площині можна розмістити 4 квадрати, 6 правильних трикутників, 3 правильні шестикутники, що мають спільну вершину і не накладаються один на одного.
За свідченням істориків, піфагорійці вміли будувати 5 видів правильних многокутників (тетраедр, гексаедр, октаедр, додекаедр, ікосаедр).
Школа Піфагора зробила геометрію наукою. Характерною рисою методики Піфагора було поєднання геометрії з арифметикою.
За філософськими поглядами Піфагор був ідеалістом, захисником інтересів рабовласницької аристократії.
У кінці Vст. До нашої ери в Греції і в її колоніях прокотилася хвиля демократичного руху. Перемогла демократія і в Кротоні. Піфагор зі своїми учнями мусив переїхати з Кротона до Тарента, а потім до Метапонта. У Цьому місті 80-річний філософ загинув.
ІІІ. Визначна теорема ПІФАГОРА,
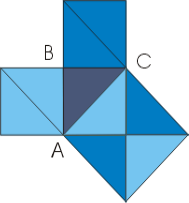
Найвизначнішою теоремою Піфагора є теорема про те, що площа квадрата, побудованого на гіпотенузі прямокутного трикутника, дорівнює сумі площ квадратів, побудованих на катетах.
|
|
|
|
Найпростіше доведення теореми одержуємо, розглядаючи прямокутний рівнобедрений трикутник. Справді, досить , просто розглянути мозаїку рівнобедрених прямокутних трикутників, щоб упевнитись в істинності теореми.. Наприклад, для трикутника АВС, квадрат, побудований на гіпотенузі АС, містить 4 трикутники, а квадрати, побудовані на катетах,- по два. Теорема доведена |
|
Отже, теорема мала інше звучання, ніж ми вивчаємо у школі.
Обернене твердження також правильне: якщо сторони а, в, с трикутника відповідають піфагорійській умові: а2+в2 = с2,
то трикутник буде прямокутним з прямим кутом, що лежить проти сторони с.
Цікавим є той факт, що для побудови господарських приміщень і видатних храмів у Вавилоні, Єгипті, Китаї майстри для отримання прямого кута креслили той самий трикутник зі сторонами 3, 4, 5.
Отже, Піфагор не знайшов цю властивість прямокутних трикутників - він тільки першим зміг узагальнити і довести її, перевести з практики в галузь науки. Як він це зробив, невідомо.
Причина такої величезної популярності теореми Піфагора триєдина: це простота - краса - значимість. І те, що існує близько 300 різних способів її доведення (геометричних, алгебраїчних, механічних і т.д.) теж свідчить про це. Знаменита теорема занесена в Книгу рекордів Гінеса. Але принципово різних ідей у цих доведеннях не існує. Деякі доведення дуже простенькі, деякі складні. Ми повинні пам'ятати, що все геніальне є простим.
Відкриття теореми Піфагором оточено ореолом цікавих легенд. Прокл, коментуючи останнє припущення першої книги „Начал" Евкліда пише: „Якщо послухати тих, хто любить повторювати старовинні легенди, то доведеться сказати, що перше доведення цієї теореми належить Піфагору; розповідають, що він на честь цього відкриття приніс в жертву богам бика". Між іншим, більш щедрі історики, одного бика перетворили в цілу сотню. І хоч ще Цицерон помітив, що будь-яке пролиття крові було вороже статуту піфагорійського ордена, легенда ця міцно зрослася з теоремою Піфагора і через дві тисячі років продовжує викликати гарячі відзиви. Так, оптиміст Михайло Ломоносов ( 1711-1765) писав „Піфагор за винайдення одного геометричного правила приніс Зевсу в жертву 100 волів. Але якби за винайдені в наш час розумними математиками правила по його забобонній звичці робити, то навряд чи в цілому світі стільки рогатої худоби знайшлося б". А ось іронічний Генріх Гейне (1797-1856) бачив розвиток тієї ж ситуації дещо інакше: „Хто знає! Можливо душа Піфагора переселилася в бідного кандидата, котрий не зміг довести теорему Піфагора і провалився із-за цього на іспитах, тоді як до його екзаменаторів вселилися душі тих биків, котрих Піфагор, зрадівши відкриттю своєї теореми, приніс в жертву безсмертним богам".
У 9 класі ми з вами будемо вивчати теорему косинусів, і я вам покажу, що теорема Піфагора є лише окремим випадком більш загальної теореми, яку можна застосувати до будь-якого трикутника. Піфагор про це ще не здогадувався...
IV. РІЗНІ СПОСОБИ ДОВЕДЕННЯ ТЕОРЕМИ ПІФАГОРА
1. Доведення із „Начал" Евкліда
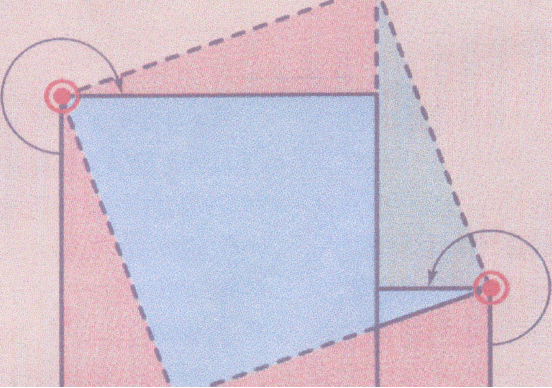
Площа квадрата, побудованого на гіпотенузі, дорівнює сумі площ квадратів, побудованих на катетах.
Суть досить складного доведення зводиться до того, що великий квадрат розбивається на дві частини, рівновеликі меншим квадратам. Але можна просто розрізати перший квадрат на такі частини, із яких складаються два інші квадрати.
Таке доведення називають «шарнірним».
2. Доведення Леонардо да Вінчі
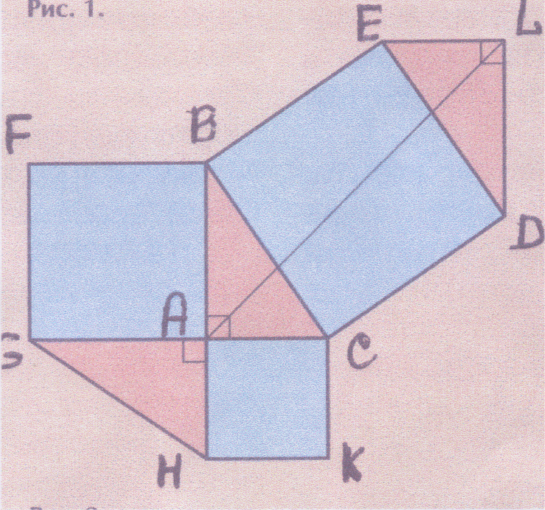
Це чисто геометричний спосіб доведення теореми Піфагора - доповнення квадратів до рівних фігур рівними їм фігурами.
∆ LDE = ∆ ABC, ∆ AGH = ∆ ABC.
Рівними будуть також чотирикутники LDCA, FBCK, ABEL, KHGF і KCBF. Отже, шестикутники KCBFGH і ACDLEB рівноскладені. Вони мають спільний трикутник ABC, а також ∆ AGH = ∆ LDE. А це означає, що
SCDEB = SCAHK+ SABFG,
або а2 + в2 = с2.
3. Доведення Бхаскари
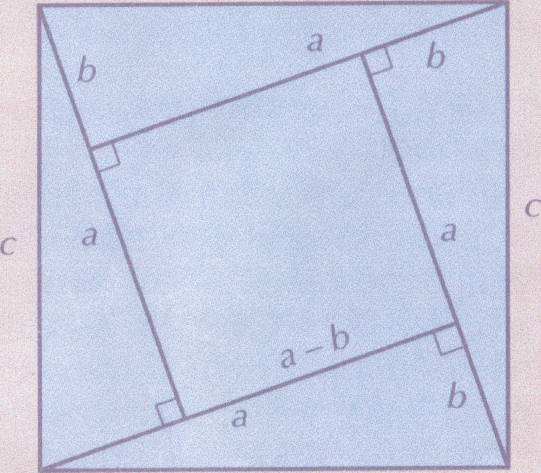
„ДИВИСЬ!"
Це доведення належить до тієї групи доведень теореми Піфагора, у яких використовуються формули для обчислення площ, тобто геометрія поєднується з алгеброю. Воно було запропоноване в трактаті індійського математика XII ст. БХАСКАРИ. Знамените це доведення тим, що весь текст до малюнка складається із єдиного слова „Дивись!"
Ми можемо самостійно довести істинність цього твердження.
с2 = (а-в)2 + 4 • ![]() ав =
ав =
а2 - 2ав + в2 + 2ав = а2 + в2. Отже,
с2 = а2 + в2.
4. Доведення з використанням подібних трикутників
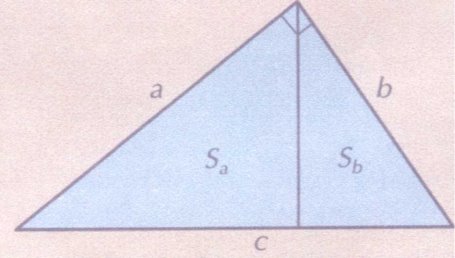
Доведення із підручника.
5. Доведення Насреддіна
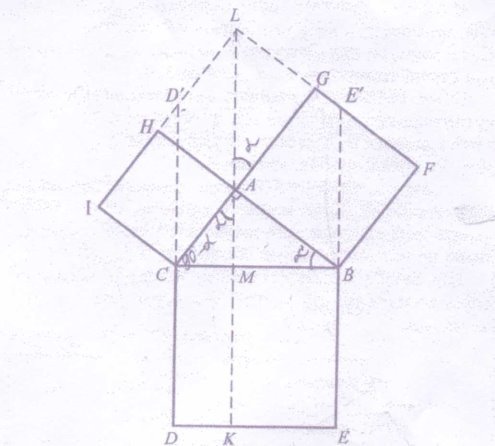
∆GAL = ∆АВС, LA = СВ, кут GAL дорівнює куту ABC і дорівнює куту САМ, тому точки L, А, М, К лежать на одній прямій. Отримали фігури з рівними площами:
SDKVC = SCALD = SCAHI = b2
Аналогічно
SKEBM= SABEL = SABFG =c2
Але
SDEBC = SDKMC + SKEBM = а2 .
Отже,
а2 = Ь2 + с2.
V. ЗНАЧЕННЯ ТЕОРЕМИ
Уявить цю теорему окремо від імені знаменитого грека вже неможливо, але співвідношення, що стверджується у цій теоремі було відоме стародавнім математикам за багато віків до Піфагора. Так про „єгипетський трикутник" зі сторонами 3, 4 і 5 ( З2 + 42 = 52) - згадується в папірусі, який історики відносять приблизно до 2000 р. до н.е. Те ж співвідношення зустрічається і на вавілонських клинописних табличках, і в давньокитайських, і в давньоіндійських трактатах.
Дякуючи тому, що теорема Піфагора дозволяє знаходити довжину відрізка, не вимірюючи його безпосередньо, вона відкриває шлях із прямої на площину, із площини - у трьохвимірний простір. Цим визначається її виключне значення для геометрії і математики в цілому.
У певному розумінні в теоремі Піфагора, як у зерні, схована вся евклідова планіметрія. Згадаємо формулу:
cos2 а + sin2 а = 1.
Це та ж теорема Піфагора, записана у тригонометричному вигляді.
Через декілька уроків ми будемо вивчати формулу, за якою знаходиться відстань між точками
А(х1; у1) і В(х2; у2) у декартових координатах.
АВ2 = (х2 - Хі)2 + (у2 - Уі)2.
Це та ж теорема, записана у декартових координатах.
VI. РОЗВ'ЯЗУВАННЯ ЗАДАЧ
1. Сторона квадрата дорівнює 5 см. Знайти довжину його діагоналей.

![]()
![]()
В

а2+а2 = х2,
2а2 = х2
х = а ![]()
2. У рівнобедреному трикутнику ABC АВ = ВС = 7 см, АС = 6 см. Знайти довжину висоти ВК.
РОЗВ'ЯЗАННЯ

![]()
![]()

ВК - висота у рівнобедреному ∆АВС, то за опорним фактом ВК і медіана, тобто АК = ![]() АС =
АС = ![]() 6 = 3 см.
6 = 3 см.
∆АВК - прямокутний, то за теоремою Піфагора
АВ2 = ВК2 + АК2,
ВК2 = АВ2 - АК2,
ВК2 = 72 - 32 = 49 - 9 = 40,
ВК= ![]() = 2
= 2![]() ( см).
( см).
Сторона ромба дорівнює 13 см, а одна з його діагоналей - 10 см. Знайти довжину другої діагоналі ромба.
РОЗВ'ЯЗАННЯ
С
![]()
![]()

А
ВО= КО = ![]() ВК = 5см. Діагоналі ромба перпендикулярні, то ∆ВОС - прямокутний і за теоремою Піфагора ВС2 = BO2 + CO2, звідки
ВК = 5см. Діагоналі ромба перпендикулярні, то ∆ВОС - прямокутний і за теоремою Піфагора ВС2 = BO2 + CO2, звідки
CO2 = ВС2 - ВО2 Тобто CO2 = ІЗ2 - 52 =169 - 25 = 144, СО= ![]() = 12 (см)
= 12 (см)
Діагональ AC = 2-12 = 24(см). Отже, друга діагональ ромба дорівнює 24 см.
4. У рівнобічній трапеції діагональ дорівнює 17 см, а висота трапеції - 8 см. Знайти середню лінію трапеції.
РОЗВ'ЯЗАННЯ
В С
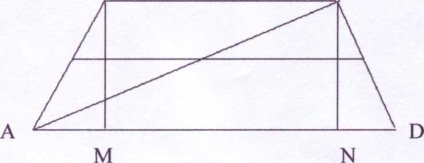
ВМ і CN - висоти трапеції, то ∆АМВ і ∆CND -прямокутні і рівні (за гіпотенузою і гострим кутом), то AM = ND =х.
Розглянемо прямокутний трикутник ANC. За теоремою Піфагора
АС2 = CN2 + AN , AN2 = AC - CN2, AN2 =172 - 82 = 289 - 64 =225,
AN = ![]() = 15(cм).
= 15(cм).
MN = AN-AM=15-x, AD = AN + ND=15+x.
BCNM - прямокутник, то ВС = MN =15 - x.
KL - середня лінія трапеції, то
KL = ![]() (ВС + AD) =
(ВС + AD) = ![]() (15-x+15 + x) = 15(см).
(15-x+15 + x) = 15(см).
Отже, довжина середньої лінії трапеції дорівнює 15 сантиметрів.
VII. ПІДСУМОК УРОКУ


про публікацію авторської розробки
Додати розробку