Урок з геометрії у 7класі на тему "Рівнобедрений трикутник та його властивості. "
Тема. Рівнобедрений трикутник та його властивості.
Мета:
- ознайомити з видами трикутника, їх властивостями;
- ознайомити з властивостями рівнобедреного трикутника і навчити застосовувати їх до розв’язування задач;
- закріпити основні поняття теми «Трикутники»;
- формувати уявлення про математику як про необхідну складову загальних знань про світ,
розвиваюча:
- розвивати самостійність, творчу і пізнавальну активність учнів;
виховна:
- виховувати увагу, активність.
Обладнання: презентація по темі «Трикутники їх види, властивості»; вислови відомих людей; макети заготовки із зображенням видів трикутників; картки із завданнями математичного диктанту і домашньої самостійної роботи; малюнки для демонстрації доведення властивостей рівнобедреного трикутника.
Тип уроку: урок формування і вдосконалення вмінь і навичок.
Хід уроку
І. Організаційний момент, ініціалізація уроку.
Оголошується тема, визначається мета діяльності.
Сьогодні ми з вами помандруємо у країну Трикутників. У цій мандрівці ми відкриємо і взнаємо багато нового і цікавого.
Безмежний океан невідомого оточує нас.
І чим більше ми знаємо, тим більше
Загадок задає нам природа.
В. О. Обручев
Те, про що ми з вами сьогодні говоритимемо на уроці геометрії, зацікавило людей ще в VI столітті до нашої ери. Трикутник як фігура є однією з перших, властивість якої людина взнала ще в глибокій старовині. Зображення трикутників зустрічаються в багатьох папірусах Давньої Греції і Давнього Єгипту. Математичний папірус Ахмеса - це староєгипетське навчальне керівництво по арифметиці і геометрії. Старогрецький учений Герон (І століття) вперше застосував знак замість слова трикутник. Навіть релігія стверджує, що трикутник – це символ бога, «яко верховного геометра». Згідно з біблійними твердженнями, Бог триликий (Бог - син, Бог - отець, Бог - дух святий). І не лише трикутник, але й число три вважають священним. А тому зосередимося і знайдемо в тайниках нашої пам'яті дещо коштовне і захопимося глибокими знаннями, які знадобляться нам сьогодні на уроці. І взагалі « Міцні знання з теми « Трикутники» - один з ключів до успіху у вивченні геометрії», (плакат з висловом висить над шкільною дошкою).
ІІ. Актуалізація опорних знань.
Фронтальне опитування.
- Яку фігуру називають трикутником?
- Що називають периметром трикутника?
- Які фігури називаються рівними?
- Які трикутники називаються рівними?
Вся або майже вся геометрія з часів «Начал» Евкліда спирається на «трьох китах» – трьох ознаках рівності трикутників. Давайте їх пригадаємо.
- Сформулювати ознаки рівності трикутників.
- Що таке медіана трикутника?
- Що таке бісектриса трикутника?
- Що таке висота трикутника?
- Які види кутів залежно від типу кутів?
- Які види трикутників залежно від довжини сторін?
- Який трикутник називається рівнобедреним?
- Який трикутник називається різностороннім?
- Який трикутник називається рівностороннім?
ІІІ. Гімнастика розуму (усні вправи)
- Визначити вид трикутника (а, б, в – за величиною кутів)
- Вказати вид трикутника в залежності від сторони
- Показати гострокутний трикутник (діти показують вирізані вдома трикутники) і довести це.
- Показати тупокутний трикутник і довести це.
- Довести рівність трикутників
б)
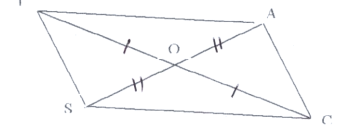 в)
в)
IV. Перевірка домашнього завдання.
1) Двоє учнів біля дошки записують розв'язання задач з домашнього завдання.
а) задача за готовим малюнком
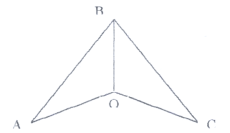
Дано : АВ=ВО, АВО=ОВС
Довести : А=О
б) Знайдіть сторони рівнобедреного трикутника, якщо його периметр 44см, а бічна сторона на 4 см більша за основу.
2) Геометричний диктант (взаємоперевірка).
І варіант II варіант
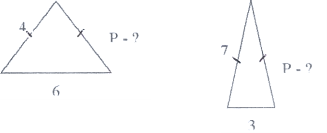 1)
1)
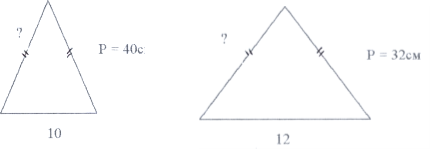 2)
2)
3)

4)
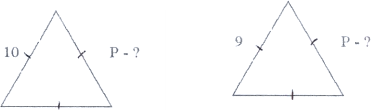
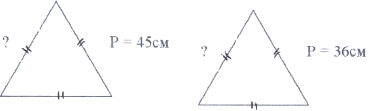 5)
5)
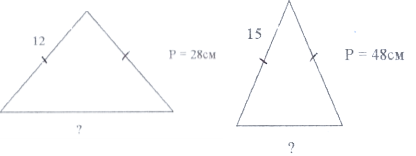
V. Вивчення нового матеріалу.
Сьогодні на уроці ми вивчимо властивості рівнобедреного трикутника:
- кути при основі рівні;
- бісектриса, проведена до основи, є медіаною і висотою.
Для доведення цих властивостей об'єднаємося у три групи.
І група «Бісектриса» доводить, що у рівнобедреному трикутнику кути при основі рівні.
ІІ група «Медіана» доводить, що у рівнобедреному трикутнику медіана, проведена до основи, є бісектрисою.
ІІІ група «Висота» доводить, що бісектриса, проведена до основи, є висотою.
Кожна група самостійно доводить протягом 5 хв. З наступним записом їх на дошці одним із учасників групи, решта учнів записують доведення у зошитах.
VI. Відпочинок на уроці
Польський математик Роман Сікорський сказав: « Математика – не тільки наука, а й мистецтво, і прекрасне мистецтво».
А зараз поговоримо про використання трикутників.
Учні мали випереджувальне домашнє завдання з поділом на групи.
І група створила малюнок-аплікацію з використанням тільки трикутників, (учні розповідають з яких трикутників створили малюнок).
II група розповідає про використання трикутників у побуті.
1) попереджувальні дорожні знаки
2) кнопки у різних приладах
3) у велосипеді
ІІІ група розповідає про використання трикутників у будівництві.
Будівельники, щоб зробити дах будинку надійним, користуються таким кріпленням кроков.
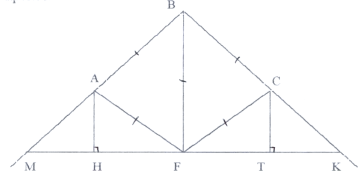
Назвіть трикутники зображені на малюнку ?
Чи є серед них прямокутні? Рівнобедрені? Рівносторонні? Аргументуйте.
VII. Формування навичок застосування властивостей рівнобедреного трикутника.
Розв'язування задач в групах,з наступним записом на дошці і в зошитах, (задачі із збірника Роєва Т.Г. «Геометрія у таблицях»).
І група. У рівнобедреному трикутнику ABC з основою АС проведена медіана ВМ. На продовженні медіани за точку М узята точка D. Довести, що ∆AMD = ∆CMD.
ІІ група. На бічних сторонах рівнобедреного трикутника ABC відкладено рівні відрізки ВМ і BN. BD - медіана трикутника. Довести, що MD = ND.
ІІІ група. На бічних сторонах рівнобедреного трикутника ABC відкладено рівні відрізки AM і CN. BD – бісектриса трикутника. Довести, що MD = ND,
VIII. Підсумок уроку.
1) Запитання до учнів класу.
а) Про властивість якого трикутниками говорили сьогодні на уроці?
б) Яку властивість мають кути при основі рівнобедреного трикутника?
в) Яку властивість має медіана; бісектриса, висота рівнобедреного трикутника?
г) Дайте визначення рівнобедреного трикутника через рівність кутів.
2) Оцінювання учнів.
ІХ. Домашнє завдання.
Виконати домашню самостійну роботу (завдання індивідуальні, різнорівневі)


про публікацію авторської розробки
Додати розробку