Урок з геометрії в 11 класі на тему "Зрізаний конус"
Урок засвоєння нових знань в 11 класі (академічний рівень). Розробка містить конспект уроку і презентацію.
Мета: ознайомити учнів із поняттям зрізаного конуса, його основними елементами та перерізами; сформувати вміння знаходити основні елементи зрізаного конуса; розвивати просторову уяву, логічне мислення, увагу, пам'ять, уміння чітко і грамотно висловлювати свою думку; виховувати наполегливість, працьовитість, акуратність, інтерес до математики.
Геометрія 11 клас
Тема. Зрізаний конус
Мета: ознайомити учнів із поняттям зрізаного конуса, його основними елементами та перерізами; сформувати вміння знаходити основні елементи зрізаного конуса; розвивати просторову уяву, логічне мислення, увагу, пам'ять, уміння чітко і грамотно висловлювати свою думку; виховувати наполегливість, працьовитість, акуратність, інтерес до математики.
Очікувані результати: учні повинні розпізнавати зрізаний конус на моделях і рисунках, будувати його зображення, елементи і перерізи, а також обчислювати основні елементи зрізаного конуса, площі перерізів і основ.
Обладнання: підручник (автор Г.В. Апостолова), мультимедійне обладнання, презентація.
Тип уроку: засвоєння нових знань.
Хід уроку
І. Організаційний етап.
ІІ. Перевірка домашнього завдання
Учні здійснюють взаємоперевірку домашнього завдання за зразком, запропонованим вчителем.


ІІІ. Актуалізація опорних знань.
- Повторення :
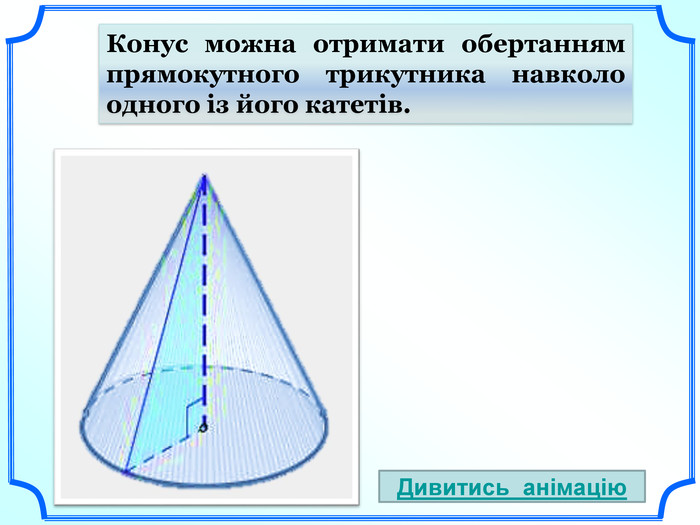
- Що називається конусом? (слайд 4)
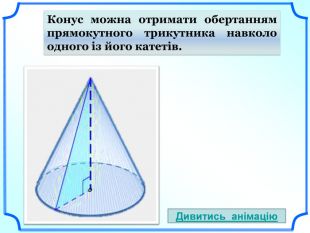
- За допомогою обертання якої фігури можна отримати конус? (слайди 5-6).
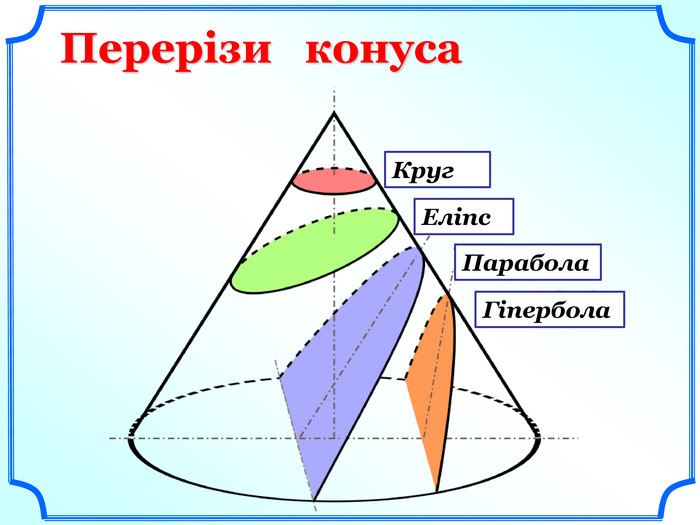
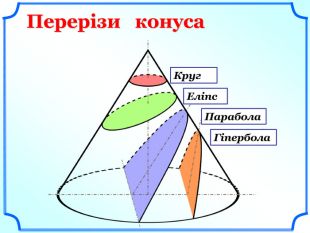
- Якими фігурами можуть буди перерізи конуса? (слайд 7).
- Розв’яжіть кросворд
1.Тіло, яке складається з круга і точки, що не лежать в одній площині і з'єднані відрізками.
2.Перпендикуляр, опущений з вершини конуса на площину основи називається…
3.Відрізки, що сполучають вершину конуса з основою.
4. У рівносторонньому конусі цей переріз - рівносторонній трикутник?
5.Пряма, яка містить висоту - це … прямого кругового конуса.
6.Точка, яка не лежить в площині основи конуса.
7. Круг, з якого складається нижня частина конуса, для нього є…
|
|
1 |
7 |
|
|
|
||||
|
|
2 |
|
|
|
|
|
|||
|
|
3 |
|
|
|
|
|
|
||
|
|
4 |
|
|
|
|
|
|
||
|
|
5 |
|
|
|
|||||
|
6 |
|
|
|
|
|
|
|
||
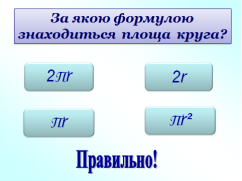
- Тести (слайди 9-13).


ІV. Мотивація навчальної діяльності.
Конус одна із фігур, що використовується в картографічних проекціях. Для більш точного проектування використовують не один конус, а серію зрізаних конусів. (слайд 14).
V. Оголошення теми, мети і завдань уроку.
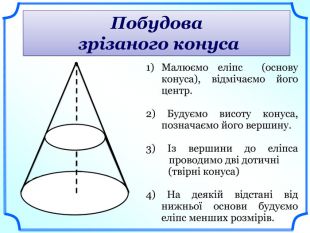
VІ. Сприймання й усвідомлення нового матеріалу.
Шкільна лекція з демонстрацією на слайдах.
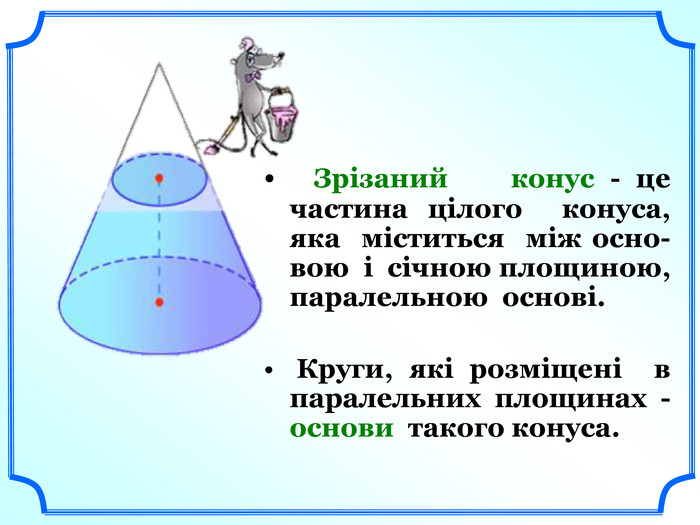
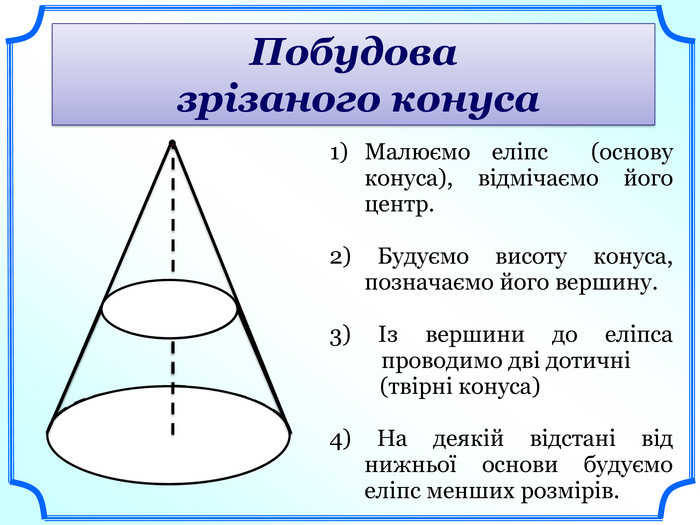
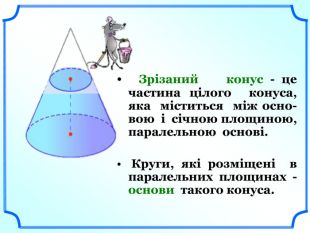
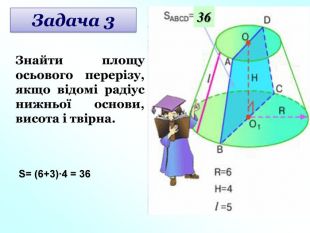
Зрізаний конус - це частина цілого конуса, яка міститься між основою і січною площиною, паралельною основі.
Круги, які розміщені в паралельних площинах - основи такого конуса. (слайд 16).
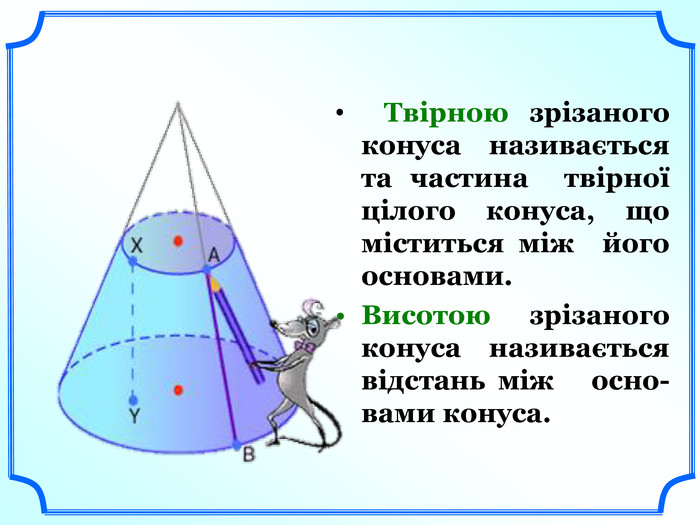
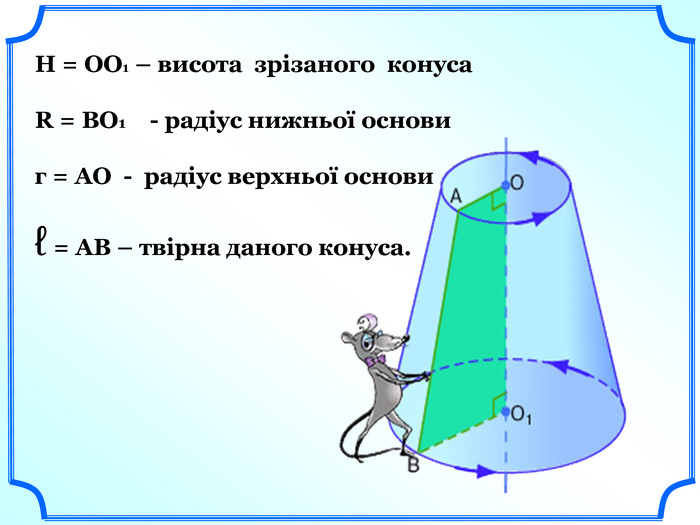
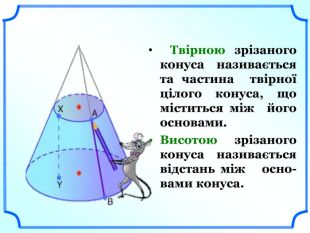
Твірною зрізаного конуса називається та частина твірної цілого конуса, що міститься між його основами.
Висотою зрізаного конуса називається відстань між основами конуса. (слайд 17).
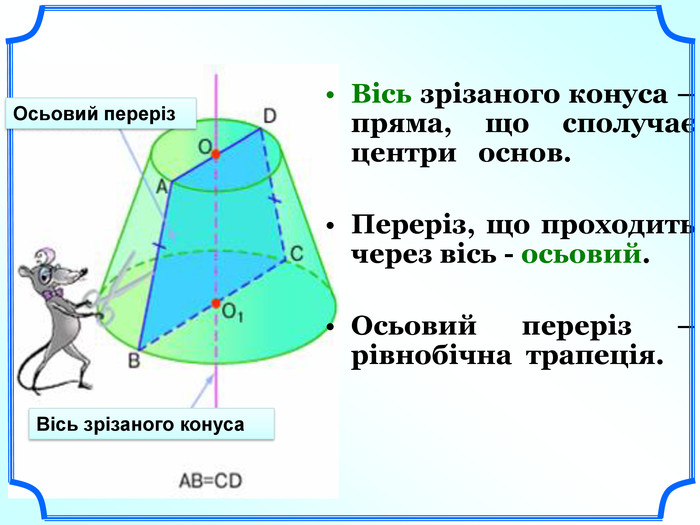
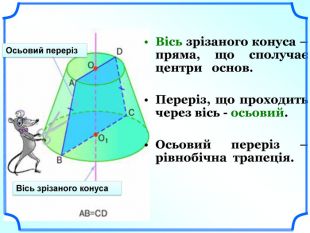
Вісь зрізаного конуса – пряма, що сполучає центри основ.
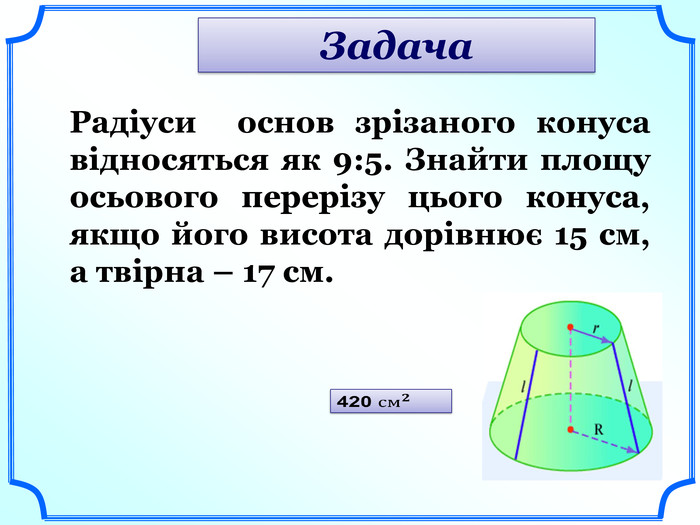
Переріз, що проходить через вісь - осьовий.
Осьовий переріз – рівнобічна трапеція. (слайди 18-19).
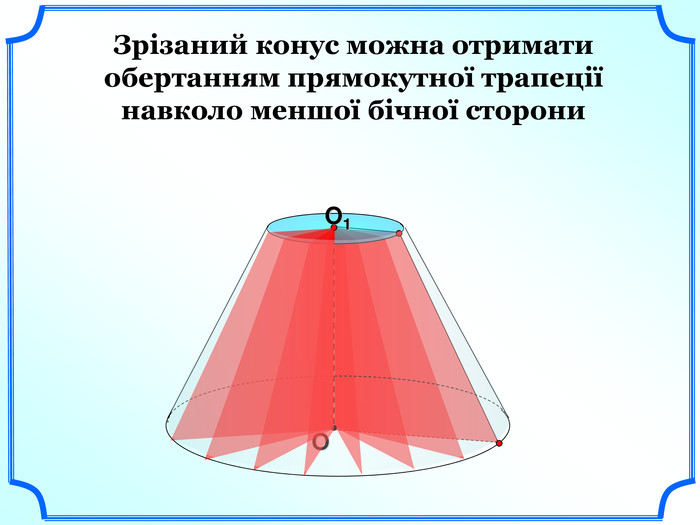
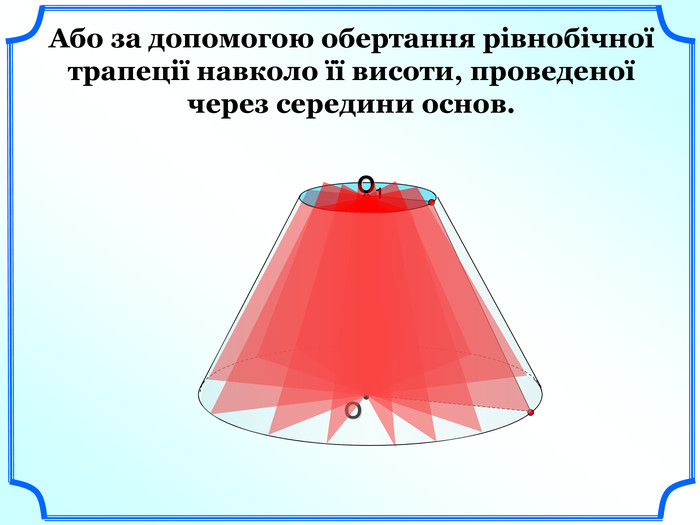
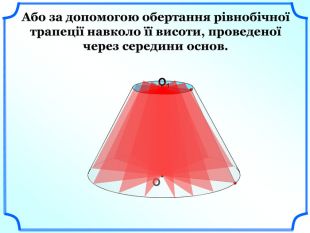
Зрізаний конус можна отримати обертанням прямокутної трапеції навколо меншої бічної сторони (слайд 20) або за допомогою обертання рівнобічної трапеції навколо її висоти, проведеної через середини основ. (слайд 21).
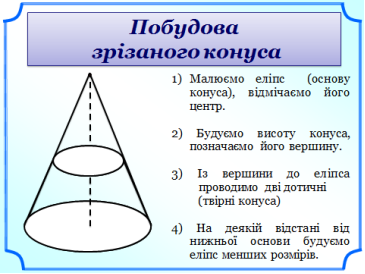
Слайд 22.
VІІ. Осмислення нового матеріалу.
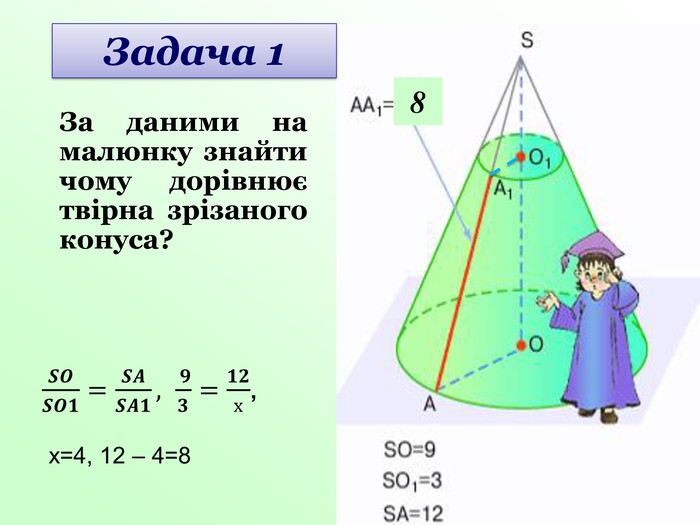
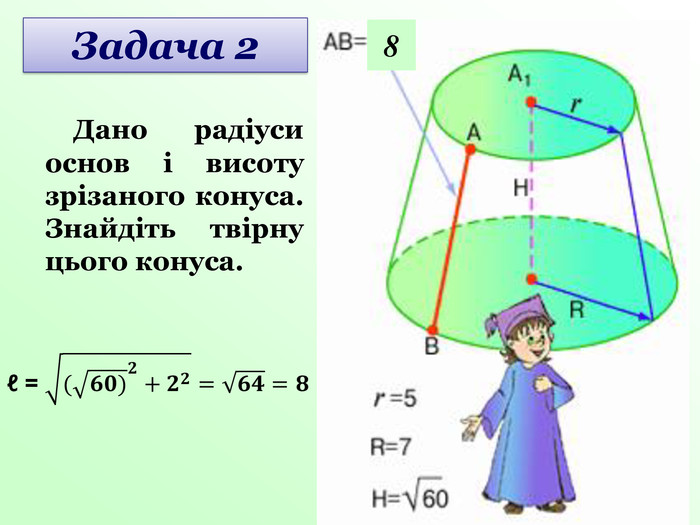
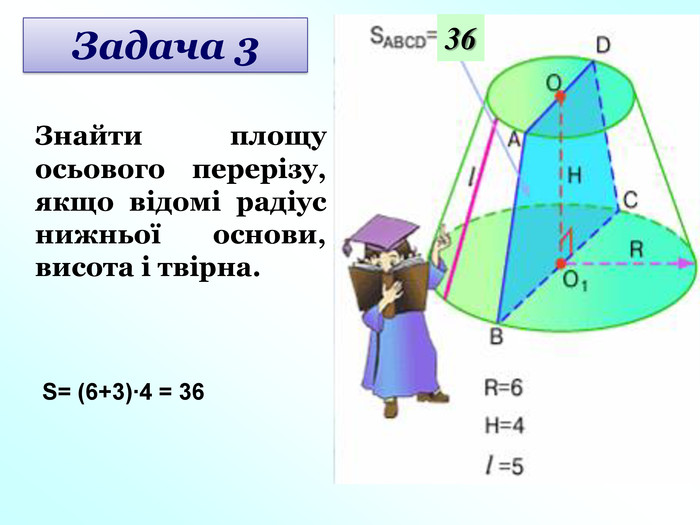
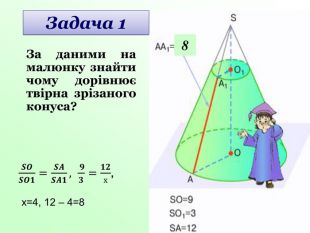
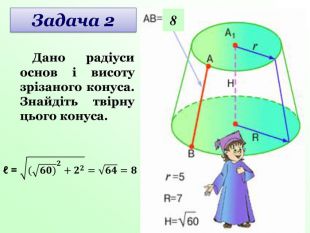
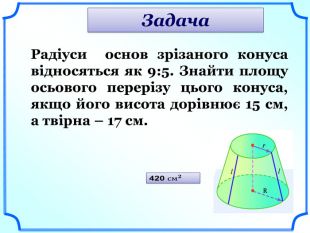
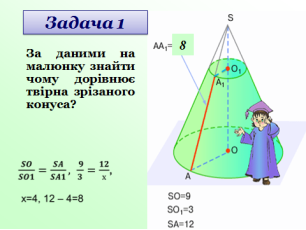
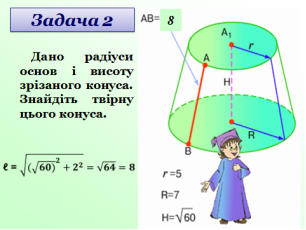
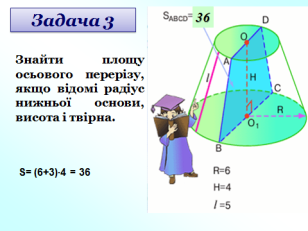
Усне розв’язування задач за готовими малюнками під керівництвом вчителя (слайди 23-25).
VІІІ. Застосування зрізаного конуса (слайди 26-42).




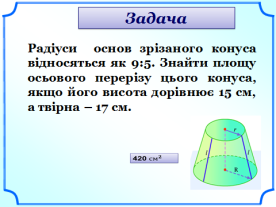
ІХ. Колективне розв’язування задач під керівництвом вчителя (слайди 43-45).


Х. Підсумок уроку (слайди 49-47).
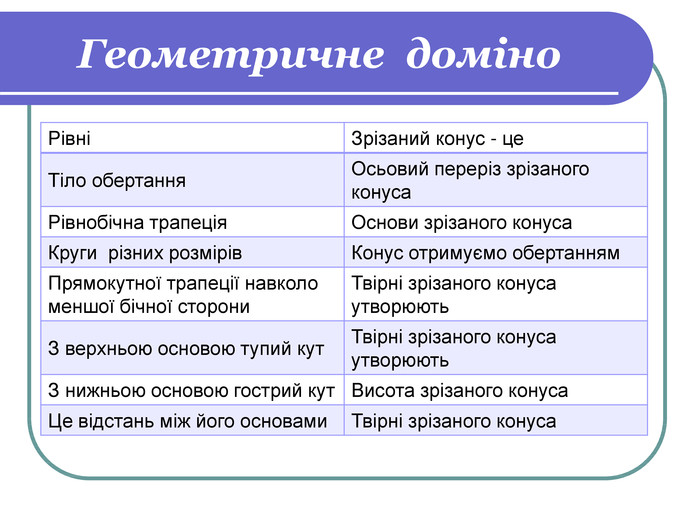
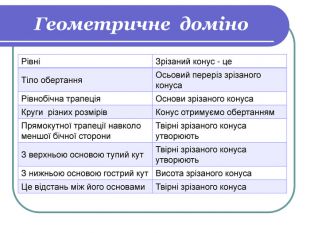
1) Геометричне доміно (учні отримують смужки паперу, в правій частині яких початок, а в лівій закінчення твердження; потрібно скласти правильні твердження).

2) Фронтальна бесіда.

ХІ. Домашнє завдання
- Вивчити §19, ст. 168.
- Виконати №№ 30(2), 31 (3).
- Яка площа верхньої частини ковпака для балу, якщо обхват голови 48 см, а висота ковпака 40 см, а відстань між двома точками кола основ -45 см?
- Додатково №35.


про публікацію авторської розробки
Додати розробку