Урок з математики для учнів 6 класу на тему: "Методи перетворення нескінченних періодичних десяткових дробів у звичайні"

Міністерство освіти і науки України

 

 

 

 

 

Відкритий урок

 

за темою:

 

Методи перетворення нескінченних

періодичних десяткових

дробів у звичайні

 

проведений  у  6   класі

 

вчителем математики

 

Задорожною Світланою Миколаївною

 

 

КЗО «Гімназія № 3» ДМР

 

2020 рік

 

Тема уроку:   Методи перетворення нескінченних періодичних десяткових дробів на звичайні. 

Мета уроку: 

навчальна: ознайомити учнів з правилами перетворення нескінченних періодичних десяткових дробів на звичайні, вивчити відповідні алгоритми, сформувати у учнів здатність до використання даних алгоритмів при обчисленні числових виразів; повторити і закріпити сумісні дії зі звичайними та десятковими дробами.

розвивальна: розвивати уміння аналізувати, висувати гіпотези, логічне та критичне мислення, увагу.

виховна: виховувати інтерес до навчання, культуру математичної мови та письма, уміння працювати в колективі, наполегливість у досягненні мети.

Форма проведення уроку: урок.

Тип уроку: урок формування нових знань та вмінь.

Обладнання: мультимедійний проектор, картки.

 

План уроку:

I.  Організаційний етап.

Перевірка готовності учнів до уроку. Створення позитивного настрою учнів.  

II. Перевірка домашнього завдання учнів.

Форма: фронтальна. Метод: демонстраційний.

Текст завдання демонструється на слайді.

III. Формування мети й завдань уроку.

Форма: фронтальна. Метод: словесний.

Оголошення учням мети і завдань уроку.

III. Мотивація учбової діяльності учнів.

Форма: фронтальна. Метод: словесний.

Одна велика людина сказала: «Без знання дробів ніхто не може признатися, що знає математику». Хто ця людина? Для того, щоб дізнатися прізвище цієї людини, треба розв’язати приклади.

Усний рахунок: (текст завдання демонструється на слайді)

Розшифруйте прізвище людини, яка сказала: «Без знання дробів ніхто не може признатися, що знає математику».

Р: ;       З: 0,8 + 0,02;      Е: ;        Р: 6,4 : 0,04;    

О: ;       А: 1,48 – 0,9;      Н: ;       І:  4,2 – 0,02;   

О:  ;      Я: 2,5 0,08;      Н: .

Розв’яжи завдання, запиши букви у таблицю, відповідно знайденим відповідям. З отриманих букв склади слово.

0,82		0,5				0,58	160			4,18	0,2
З	Е	Н	О	Н		А	П	О	Р	І	Я

Зенон Елейський (490—430 до н. е.) — давньогрецький філософ елейської школи, відомий своїми апоріями або парадоксами. А що це таке, ми дізнаємося трохи пізніше.

IV. Актуалізація опорних знань учнів.

Форма: фронтальна, індивідуальна. Метод: опитування.

Бесіда:

1) Як перетворити звичайний дріб у десятковий?

2) У якому випадку нескоротний дріб можна перетворити в десятковий?

3) Дайте означення нескінченного періодичного десяткового дробу?

4) Що називають періодом дробу?

5) Які види нескінченних періодичних десяткових дробів ви знаєте?

6) Як помножити два звичайних дроби?

7) Як поділити два звичайних дроби?

8) Як додати або відняти дроби з різними знаменниками?

9) Як порівняти два десяткових дроби?

10) Як додати або відняти два десяткових дроби?

11) Як помножити два десяткових дроби?

12) Як поділити два десяткових дроби?

V. Вивчення нового матеріалу.

Форма: фронтальна, індивідуальна.

Метод: проблемний.

1. Завдання класу:  (текст задачі демонструється на слайді)

 Знайдіть значення виразу: .

Розв’язання:

2. Виявлення причини утруднення і постановка мети діяльності.

– Чому ви не змогли розв’язати  завдання? (Тому, що ми не вміємо ділити періодичні дроби).

– Як ви думаєте, що ж нам робити? (Знайти спосіб перетворення нескінченних періодичних десяткових дробів на звичайні, бо всі дії над звичайними дробами ми вміємо виконувати).

– Сформулюйте мету уроку. (Вивести алгоритм перетворення нескінченних періодичних десяткових дробів на звичайні).

3. Побудова проекту виходу з утруднення.

Пояснення вчителя:

Позначимо х = 0,(2) = 0,222… 

Помножимо ліву і праву частину цієї рівності на 10, маємо: 10х = 2,222…

Віднімемо отримані рівності, маємо:

9х = 2, х = . Отже,  0,(2) = . Сформулюйте правило:  як перетворити нескінченний десятковий чисто періодичний дріб у звичайний?

Чисто періодичний десятковий дріб дорівнює звичайному дробу, чисельником  якого є період даного дробу, а знаменником  – цифра 9, що записана стільки разів, скільки цифр у періоді дробу.

  Наприклад:  0,(3) = ;    0,(81) = .

 Самостійне розв’язання у зошиті:   1,(121) = 1.

- Як перетворити змішаний нескінченний періодичний десятковий дріб на звичайний?

Позначимо х = 0,4(6) = 0,4666… 

Помножимо ліву і праву частину цієї рівності на 10, маємо:

10х = 4,666…

Помножимо ліву і праву частину цієї рівності на 100, маємо:

100х = 46, 666…;   10х =   4,666…

Віднімемо отримані рівності, маємо:

90х = 42, х = . Отже,  0,4(6) = . Сформулюйте правило:  як перетворити змішаний нескінченний десятковий  періодичний дріб у звичайний?

Для того щоб перетворити змішаний нескінченний періодичний десятковий дріб на звичайний, треба від числа, що стоїть до другого періоду, відняти число, що стоїть до першого періоду. Потім записати цю різницю чисельником, а в знаменнику записати цифру 9 стільки разів, скільки цифр у періоді, а після дев’яток дописати стільки нулів, скільки цифр стоїть між комою і першим періодом.

Наприклад:  0,11(7) = ;   0, 14(23) = ;  

Самостійне розв’язання у зошиті:   1(36) =

Отже, тепер ми можемо розв’язати приклад , розглянутий на початку уроку:

4. Фізкульхвилинка.

Отже, ми вивели формулу, необхідну для нашої роботи, але керівництво нашої гімназії зацікавлене тим, щоб його учні були здоровими і добре працювали. Тому з метою  попередження втомлюваності і перевантаження організму, для покращення мозкового кровообігу, виконаємо фізкультхвилинку.

V. Формування умінь та навичок учнів.

Форма: фронтальна, індивідуальна. Метод: робота в парах.

1. Розв’язування біля дошки:

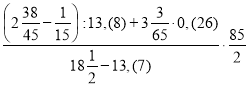
 2. Робота в парах:

Самостійне розв’язання у зошитах із самоперевіркою по еталону.

Тексти різнорівневих завдань та еталони їх розв’язання демонструються на слайдах.

№ 1 (для учнів, що  слабо встигають) (на 7 балів)

1. Подайте нескінченний десятковий періодичний дріб у вигляді звичайного дробу:

а) 0,(1) ;  б) 0,(36);  в) 0,1(01).

2) Порівняй числа: 0,(2) і  

Еталон:

1. Подайте нескінченний десятковий періодичний дріб у вигляді звичайного дробу:

а) 0,(1) = ;  б) 0,(36) = ;  в) 0,1(01) = .

2) Порівняй числа: 0,(2) =  

№ 2 (для учнів із середніми здібностями) (на 9 балів)

1) Порівняй числа: 0,11(12) і .

2) Обчисли: (2,(6) + 1,8(3)) : 1,5.

Еталон:

1) Порівняй числа: 0,11(12) < ,  бо 0,11(12) =

2) Обчисли: (2,(6) + 1,8(3)) : 1,5 =

№ 3 (для учнів з високим рівнем знань) (на 11 балів)

 Обчисли: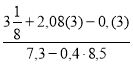

Еталон: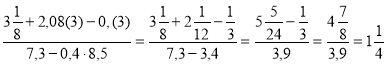

      Учні самостійно перевіряють виконану роботу, звіряючись з еталоном, виправляють помилки і заповнюють аркуш накопичення оцінок.

VI. Включення в систему знань і повторення.

Форма: фронтальна. Метод: розв’язування біля дошки.

Апорія Зенона «Ахілл та черепаха».

Ахілл, відомий серед героїв швидкістю свого бігу, змагається з черепахою. Його швидкість в 10 раз більша за швидкість черепахи. Вони стартують одночасно, але при цьому точка, звідки починає рух черепаха, знаходиться попереду місця старту Ахілла на 1 км. Бігун швидко долає відстань до точки, звідки починала шлях черепаха, але за цей час неспішна тварина все-таки встигла проповзти ще небагато вперед. Ахілл нестримно долає і цю малу відстань, але черепаха знову устигає відповзти трохи вперед. Ахілл знову переноситься в місце, де знаходилася черепаха, але та знову здолала деяку долю шляху. І так триває до нескінченності: Ахілл все ближче до черепахи, але ніколи не може її не лише перегнати, але навіть наздогнати. Як це так?

VII. Історична довідка. Доповідь учителя про апорії Зенона.

VIII. Підведення підсумків уроку.

Форма: фронтальна.

Метод: словесний.

Підведемо підсумок уроку.

 Оголошення оцінок, які отримали учні.

IX. Повідомлення домашнього завдання.

Форма: фронтальна.

Метод: словесний.

п. 2.18 № 566, 569. Додатково розв’яжіть задачу про Ахілла та черепаху.

X.  Рефлексія діяльності.

Форма: фронтальна.

Метод: словесний.

Бесіда:

– З якими поняттями ми сьогодні познайомилися?

– З яким утрудненням виведені правила допомогли справитися?

– Чому ми училися на уроці?

– Підніміть руки, якщо згодні з твердженням.

Я знаю, як перетворити нескінченний періодичний десятковий дріб на звичайний.

Я знаю, але допускаю обчислювальні помилки.

У мене залишилися незрозумілі  питання.

 

 

 

 

Картка самоконтролю Прізвище __________________________    1 Домашнє завдання   2 Усний рахунок   3 Усні питання   4 Робота в парах     Всього (балів)   Картка самоконтролю Прізвище __________________________    1 Домашнє завдання   2 Усний рахунок   3 Усні питання   4 Робота в парах     Всього (балів)   Картка самоконтролю Прізвище __________________________    1 Домашнє завдання   2 Усний рахунок   3 Усні питання   4 Робота в парах     Всього (балів)   Картка самоконтролю Прізвище __________________________    1 Домашнє завдання   2 Усний рахунок   3 Усні питання   4 Робота в парах     Всього (балів)   Картка самоконтролю Прізвище __________________________    1 Домашнє завдання   2 Усний рахунок   3 Усні питання   4 Робота в парах     Всього (балів)   Картка самоконтролю Прізвище __________________________    1 Домашнє завдання   2 Усний рахунок   3 Усні питання   4 Робота в парах     Всього (балів)

Картка самоконтролю Прізвище __________________________    1 Домашнє завдання   2 Усний рахунок   3 Усні питання   4 Робота в парах     Всього (балів)   Картка самоконтролю Прізвище __________________________    1 Домашнє завдання   2 Усний рахунок   3 Усні питання   4 Робота в парах     Всього (балів)   Картка самоконтролю Прізвище __________________________    1 Домашнє завдання   2 Усний рахунок   3 Усні питання   4 Робота в парах     Всього (балів)   Картка самоконтролю Прізвище __________________________    1 Домашнє завдання   2 Усний рахунок   3 Усні питання   4 Робота в парах     Всього (балів)   Картка самоконтролю Прізвище __________________________    1 Домашнє завдання   2 Усний рахунок   3 Усні питання   4 Робота в парах     Всього (балів)   Картка самоконтролю Прізвище __________________________    1 Домашнє завдання   2 Усний рахунок   3 Усні питання   4 Робота в парах     Всього (балів)