Урок з прикладними задачами: Розв'язування задач на дослідження функцій за допомогою похідної.

Урок

з прикладними задачами

10клас  

       ВЧИТЕЛЬ: Рєпкіна Валентина Єгорівна,

КЗ» НВК№2 м .Покров Дніпропетровської області»

ТЕМА:Розв’язування задач з теми: «Дослідження функцій за допомогою    похідної» .

МЕТА: Показати старшокласникам, що прикладні задачі є діяльними; вони моделюють життєві ситуації; будуються на актуальному матеріалі; потребують застосування загальних навчальних знань , вмінь та навичок.

Закріпити знання похідної, таблиці похідних, правила диференціювання.

Формувати підприємницьку компетентність, вміння слухати, робити висновки.

Розвивати логіку мислення, інтуіцію, культуру спілкування.

 І.Актуалізація опорних знань:

1. Математичний бій.(Повторення теоретичного матеріалу)
2. Знайди помилку(Повторення таблиці похідних та правил диференцювання)

ІІ. Мотивація, повідомлення теми, задач уроку.

Сценка: Зустрілися два друга. Перший каже: Я вирішив купити ділянку певної площі. Хотів би побудувати будинок прямокутної форми з площею 400м² , межі ділянки у вигляді прямокутника повинні знаходитись від будинка на відстані 36 і 16 м. Ось, думаю: Які розміри потрібно надати будинку , щоб площа ділянки була найменшою. Друг, який працює в проектній фірмі відповідає: Я допоможу тобі розвязати це питання.

ВЧИТЕЛЬ: Як?

     Перед людиною часто стає питання: Як зробити ремонт, щоб найменше затратити коштів? Як побудувати басейн певної площі з найменшими витратами на облицювання і такі інші? Щоб відповісти на ці питання, ми сьогодні будемо вчитися складати функції та застосовувати похідну в їх дослідженні, тобто розвязувати прикладні задачі.

ІІІ. Розв’язування задач прикладного змісту.

    №1. Визначити розміри такого відкритого басейну з квадратним дном і об’ємом 32м³ , щоб на обліцьовування його стін і дна було витрачено найменшу кількість матеріалу.(біля дошки)

Розв’язання

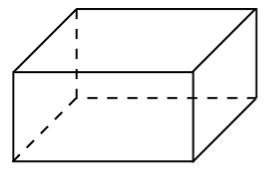
Позначимо довжину сторони основи х, висоту у. Тоді V=х²у,

 х²у =32.

Площа бічної поверхні басейну разом з площею дна:

S(x) =x²+4ху,

 S(x) =x²+,

S¹(х) =2х- ,

2х - =0,

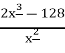=0,   х≠0.

2х³ =128,

Х³=64,

Х=4.

   X_min=4,  У_min= =2.

 Відповідь: 4м і 2м.

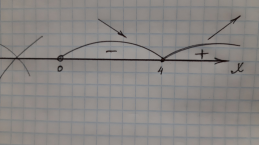
 №2. Кількість хворих Р(t) під час епідемії грипу змінювалась з часом t (t вимірюється днями) від початку вакцинації населення за законом

Р(t).

 Визначте час максимуму захворювання, інтервали його зростання і    спадання та побудуйте графік заданої функції.

А тепер допоможемо розв'язати задачу, яка виникла на початку уроку.

         №3 Для будівництва будинку прямокутної форми, зображеного  на плані прямокутником з площею 400м²відведено ділянку у вигляді прямокутника , межі якої повинні знаходитись від будинку на відстані 36м

16 м. Які розміри потрібно надати будинку, щоб площа ділянки була найменшою?

Домашнє завдання: Повторити §5, п.37, 39, 40, 41.

                                  Розв’язати задачу:

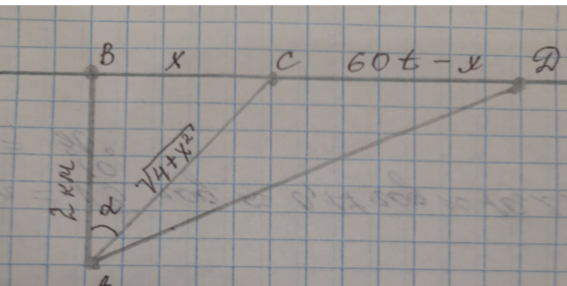
 Вантажівка , яка на початку руху знаходиться в т. В і прямує до пункту D по шосе зі швидкістю 60км/год, порушує правила дорожнього руху. На початку руху полем патрульний мотоцикл , який знаходиться в пункті А, що за 2 км від шосе , може розвивати швидкість 40км/год. А на шосе швидкість мотоцикла складає 80км/год. Під яким кутом α до напрямку АВ слід виїхати патрульному мотоциклу , щоб якомога швидше наздогнати вантажівку? За який мінімальний час патруль наздожене порушника?