Урок з теми: "Квадратична функція, її властивості та графік". Алгебра 9 клас

 

 

 

 

 

Квадратична функція, її властивості та графік

(Розробка навчального заняття. Алгебра, 9 клас)

                                   

 

 

Робота
учителя математики

 Фурсівського ліцею-гімназії
Ярошенко Олени Миколаївни
 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Тема уроку. Функція , її властивості та графік.

Мета уроку:  1)сформувати знання учнів про означення, вид графіка та алгоритм побудови графіка квадратичної функції, сформу­вати первинні вміння розпізнавати квадратичну функцію серед інших елементарних функцій, знаходити координати вершини та напрям віток графіка квадратичної функції, виконувати побудову графіка квадратичної функції за ви­вченими алгоритмами; вдосконалити навички розв’язування вправ на  дослідження квадратичної функції,  побудову її графіка, перетворення графіків функцій;

2) розвивати  мислення, пам'ять, кмітливість, увагу, ініціативність, самостійність, вміння об’єктивно проводити самоконтроль власної діяльності;

3) виховувати культуру мовлення,  дисциплінованість, навички колективної роботи та співпраці ,формувати пізнавальний інтерес.

Тип уроку: формування знань, вироблення первинних умінь.

Наочність та обладнання:  мультимедійний проектор, комп’ютерна презентація, картки із тестовими завданнями, математичний кросворд, оцінний аркуш.

Хід уроку

І. Організаційний етап

ІІ. Мотивація навчальної діяльності

 
Учитель. Пам’ятаєте, у минулому році ми були на екскурсії в м. Умань  та відвідали фентезі-парк «Нова Софіївка»? Це абсолютно новий об’єкт, який виріс поруч із історичним дендропарком. У «Новій Софіївці» поєднуються природа, сучасне і традиційне мистецтво, різні світові культури, які представлені унікальними композиціями та арт-об’єктами. Один із них фонтан, утворений рядом дугоподібних  струменів води. Краса, ідеальна рівність дуг утворюють справжній водяний тунель по якому хочеться пробігти ще раз і ще раз.

 Чи не нагадує вам траєкторія руху струменів графік однієї із функцій, які ви вивчали у 8 класі?

Інтерактивна вправа «Асоціативний кущ».

Учитель. Парабола. Працюємо над цим терміном. Ви повинні називати усе, що виникає у пам’яті стосовно цього слова, спочатку найстійкіші асоціації, а потім — другорядні.

1.     Як називається такий графік? (Парабола)
2.     Як називається функція графіком якої є парабола? (Квадратична)
3.     Запишіть аналітичний вигляд квадратичної функції( )
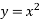4.     Який вигляд має графік квадратичної функції у системі координат?

 

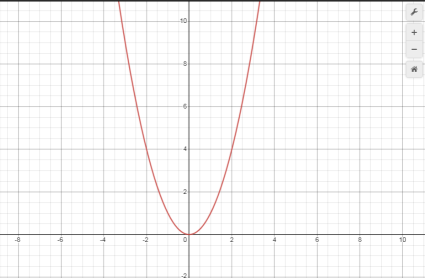
5.     Як розміщені вітки параболи?( Вверх)

Учитель. А траєкторія руху струменя води в фонтані – це парабола вітками вниз. І не тільки така траєкторія зустрічається повсякчас у нашому житті. Тому сьогодні з’ясуємо, яка функція описує параболу та навчимося будувати її графік та розглянемо її властивості.

 

ІІІ. Оголошення теми та мети уроку.

Учитель. Сьогодні ми знайомимося із однією із найважливіших функцій алгебри квадратичною.

Означення. Функцію, що задається формулою виду, де x – незалежна змінна,   a,b,c   - деякі числа, причому , називають квадратичною функцією.

Прикладами квадратичної функції є:

Залежність площі квадрата S від довжини чого сторони m

Залежність площі круга S від його радіуса R

, де

Залежність висоти. На якій перебуває тіло, що кинуто вертикально вгору з початковою швидкістю , від часу руху тіла

Інженерні розрахунки і практика засвідчують, що споруди та конструкції (ферми мостів, арки), обриси яких нагадують параболу або гіперболу, мають підвищену міцність. Властивості квадратичної функції враховують при виготовлені параболічних дзеркал, прожекторів, шаблонів для виробництва деталей тощо.

За допомогою квадратичної функції можна описати низку різноманітних процесів, явищ у природі, в побуті, на виробництві. На приклад, рух тіла , що вільно падає, описує функція виду y=4,9x², яка дає, зокрема, можливість знайти відстань у ( в метрах ), яку пролетить тіло за x  секунд.

Учитель. Оцініть знання з оголошеної теми до та після того, як ви почали її вивчати. Заповніть стовпчики за критеріями: що ви знаєте, що хотіли дізнатись та що нове дізналися?

Учні. Оцінюють свої знання з даної теми на початок уроку та заповнюють таблицю. Особливо  стовпчик Про що Хочу дізнатися?

Що Знаю?	Про що Хочу дізнатися?	Про що Дізнався?

IV. Розв’язування вправ.

Учитель. Визначте і обґрунтуйте, чи є квадратичною функція y(x), якщо:

 

Учні. Читають формулу функції, обгрунтовують чи ця функція квадратични а на основі означення.

Учитель. У фізиці існує багато задач для яких потрібно змоделювати рух тіла кинутого вгору, або тіла, кинутого з висоти. Оскільки траєкторією руху є парабола, потрібно вміти її будувати. Головне, визначити координати вершини. З’ясовуємо як саме. Застосуємо метод виділення квадрата двочлена. Згадаємо формули скороченого множення квадрат різниці та квадрат суми, які використовують у такому методі:

 

 

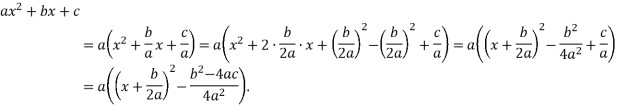
Розкриємо дужки та скоротимо дріб у другому доданку. Маємо:

Отже, функцію можна записати у вигляді позначивши Де () це координати вершини параболи. Якщо їх відповідно позначити  , то координатами вершини параболи .

Проаналізуйте ординату вершини і згадайте формулу дискримінанта квадратного рівняння. (Учні записують формулу  і замінюють чисельник дробу буквою .

Формулу

Учитель. Якщо  обчислили  абсцису вершини за формулою, то ординату можна обчислити іншим способом, тобто не за формулою. Запропонуйте як?

Учні. Повинні згадати як знаходити ординату точки через підстановку значення абсциси у формулу функції.

(якщо в учнів виникають труднощі, задаємо допоміжні запитання:

Як обчислити значення функції, якщо знаємо значення аргументу?

Якщо точка належить графіку функції, то її координати перетворюють аналітичний запис функції у правильну рівність)

Учитель.

Завдання №1.  Знайти координати ( вершини параболи застосувавши формули :

1); 

Учні. Учні об’єднані перед уроком у 5 різнорівневих  груп. Для групи  з високим рівнем навчальних досягнень в цей час пропонуємо знайти координати вершини параболи виділенням квадрата двочлена:

По закінченні виконання завдання кожний представник групи повідомляє результати роботи групи. Всі звіряють відповіді, виправляють помилки.

Завдання №2.  Скласти алгоритм побудови параболи , розташувати кроки у правильній, на вашу думку, послідовності. Скористатися рисунками-кроками з підручника ст.151.

Складений алгоритм оголошує та група, яка перша впоралася із завданням. Учні з інших груп ставлять запитання про доцільність того чи іншого кроку алгоритму. Учитель координує процес диспуту.

Завдання №3. Тренуймося №1 ст.154. Побудувати за складеним алгоритмом графік функції 5)

Завдання 5) виконують групи середнього та достатнього рівня навчальних досягнень, завдання 8) виконують дві групи високого рівня. Побудовані графіки по одному учню із групи демонструють на дошці і покроково описують хід виконання завдання. Разом виправляють помилки та допомагають на кожному етапі.

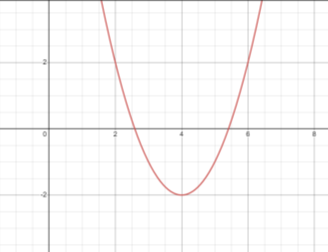
Завдання №4. Користуючись графіком функції, визначте координати вершини параболи, рівняння осі симетрії параболи. (Рисунки створені у графічному калькуляторі https://www.desmos.com/calculator)

 

 

 

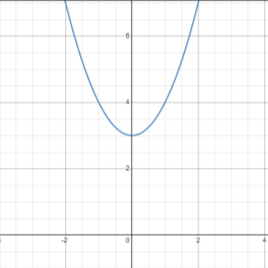
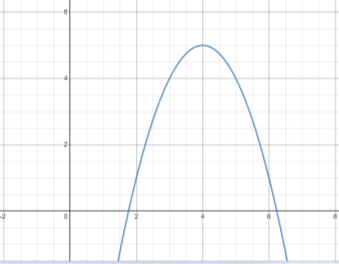
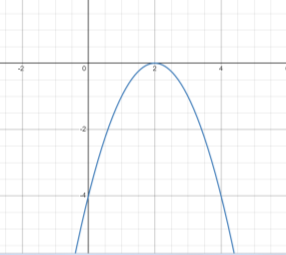
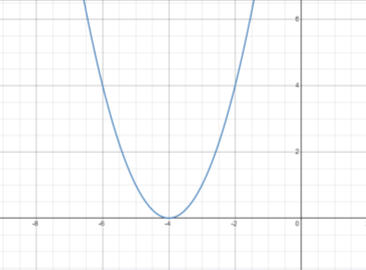
Учитель. Згадаємо правила побудови графіків функцій за допомогою геометричних перетворень.

Завдання №3. Співставте функцію з видом перетворення графіка функції y=f(x):

1.     Паралельне перенесення графіка функції y=f(x) уздовж осі Oy;
2.     Паралельне перенесення графіка функції y=f(x) уздовж осі Ox;
3.     Розтяг графіка функції y=f(x) у k разів уздовж осі Oy , якщо k>1;

Стиск  графіка функції y=f(x) у разів уздовж осі Oy, якщо 0<k<1;

4.     Симетричне відображення графіка функції y=f(x) відносно осі Ox.

1.   y=f(x)+a;
2.    y=f(x+a);
3.    y=k*f(x);
4.   y=-f(x).

Учні. Завдання виконують усно, пояснюють як відбувається перетворення графіків.

Учитель. Побудова графіка квадратичної функції потребує багато часу, але науковці Каліфорнійського університету створили комп’ютерний симулятор, який допомагає їх будувати в один клік.

Завдання №4. (https://phet.colorado.edu/uk/simulations/graphing-quadratics). За допомогою симулятора побудуйте графіки функцій:

1)

2)

3) 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

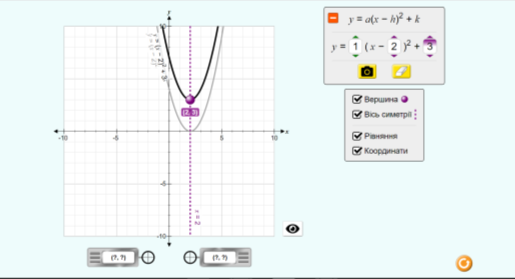
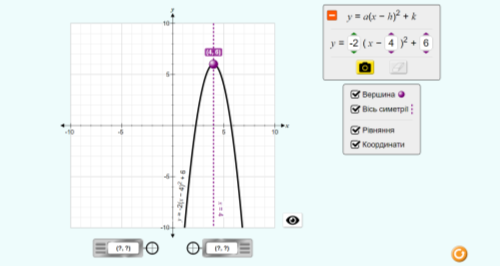
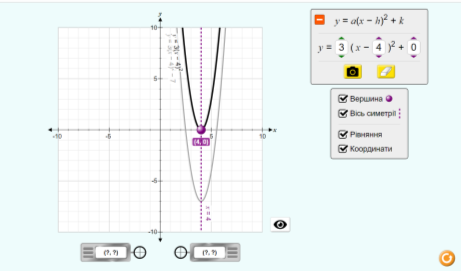
Для кінцевої функції знайдіть:

1.       координати вершини параболи;
2.     написати алгоритм перетворення початкового графіка функції в кінцевий;
3.     найбільше(найменше) значення кожної функції.

Завдання №5.Поєднати функцію, графік та об’єкт.

1.     струмінь моди музичного фонтану;
2.     траєкторія польоту м’яча;
3.     форма моста;
4.     траєкторія польоту каменя, кинутого з катапульти.

 

 

 

 

 

 

 

 

 

 

 

 

V. Рефлексія

Учитель. Підведемо підсумки уроку. Відкрийте таблицю ЗХД та доповніть записами, особливо стовпчик Про Що дізнався? Проаналізуйте свою діяльність на уроці та поділіться враженнями із однокласниками.

Учитиель. Пропонує фрази, які діти  повинні закінчити. 

Учні. Кожен закінчує речення. Важливо, щоб усі учні виконали дане завдання, навіть найслабші. Учень сам повинен оцінити, на якій сходинці він виявився в результаті діяльності під час уроку, тобто оцінити досягнуті результати.

Я познайомився з ...
Було непросто ...
Я домігся ...
В мене вийшло ...
Хотілося б ...
Мені запам'яталося ...
Я спробую ...

 VI. Домашнє завдання.

Завдання №1.“Ромашка Блума”. Придумати :

1. Просте запитання, яке розпочинається словами Що?, Хто? Де?( Що є графіком квадратичної функції? Хто винайшов джампери? Де знаходиться колонада «Відлуння»?)
2.  Уточнююче запитання, яке розпочинається словами: Правильно я зрозумів..., Ти вважаєш, що...(Правильно я зрозумів, що гафік квадратичної функції можна побудувати методом геометричних перетворень? Ти вважаєш, обовязково виділяти квадрат двочлена для знахоження координат вершини параболи?)
3.  Пояснююче запитання, яке розпочинається словами: Чому? Навіщо?(Чому супутникова антена має параболічну поверхню? Навіщо записувати рівняння х=х0 для побудови параболи?)
4.  Оцінююче запитання, яке потребує оцінити проблему.( Чи допоможе побудова графіка квадратичної функції знайти найбільшу відстань польоту снаряда?)
5.  Практичне запитання, у якому поставлене завдання, яке потрібно вирішити (Як описати формулою струмінь води декоративного фонтану, якщо знаєш що вода піднімається на найбільшу висоту 2 м?)
6. Творче запитання, у якому можна проявити свою найдивнішу фантазію (Що буде, якщо поверхню оптичного телескопа покрити сонячними панелями?)

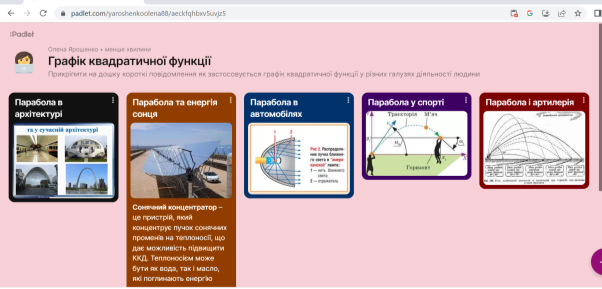
Завдання №2 (довгострокове). Створити на дошці Padlet (https://padlet.com/yaroshenkoolena88/aeckfqhbxv5uvjz5) коротке повідомлення-дослідження як графік квадратичної функції можна використовувати в різних сферах діяльності людини.