Урок з теми "Лінійна функція, її графік і властивості"

Про матеріал

Даний конспект уроку з елементами гри «Лінійна функція, її графік та властивості» може бути використаний на уроках алгебри в 7 класі при вивченні теми «Функції» в курсі алгебри 12-річної школи.

Перегляд файлу

Урок № 54 Клас______ Дата_________

Тема. Лінійна функція, її графік та властивості

Мета: ознайомити учнів із означенням лінійної функції та сформувати знання про графік та властивості лінійної функції; виробити первинні вміння будувати та читати графік лінійної функції; активізувати пізнавальну діяльність учнів; виховувати інтерес до вивчення математики.

Тип уроку: засвоєння нових знань.

Хід уроку

І. Організаційний момент

Взаємоперевірка готовності учнів до уроку.
Відсутні

II. Перевірка домашнього завдання № 823, 826, 828

III. Актуалізація опорних знань Гра «Математичне лото»

Ігровий момент «Найрозумніший»

Відповідність між змінними у та х, за якої кожному значенню змінної х відповідає єдине значення змінної у — це... (Функція).
Змінна х — ... (Аргумент).
Змінна у — ... (Функція, значення функції).
Усі значення, яких набуває аргумент, утворюють... (Область визначення функції).
Усі значення, яких набуває функція при аргументах, взятих з області визначення функції, утворюють... (Область значень функції).
Множина усіх точок координатної площини, абсциси яких дорівнюють значенню аргументу, а ординати — відповідним значенням функції, називається... (Графіком функції).
Коефіцієнти многочлена 3х³ – 2х² – х – 2 — це... (3; -2; -1; -2).

ІV. Гра «Математичне лото»

( 2; -6 )				функція
x-будь-яке число, окрім		абсциса
	область значень функції		( 3; 3 )

аргумент		x-будь-яке число, окрім		( 2; -6 )
	( 2; 5 )
графік функції			ордината

Текст завдання

Усі значення, яких набуває залежна змінна утворюють (область значень функції).
Графіку функції 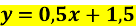належить точка (3;3)
Незалежна змінна називається (аргумент)
Функція задана формулою 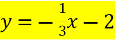. Знайдіть значення функції, якщо значення аргументу = 15 (- 7 )
Геометрична фігура, що складається з усіх точок координатної площини, абсциси яких дорівнюють значенням аргументу, а ординати відповідним значенням функції (графік функції)
Функція задана формулою ( x-будь-яке число, окрім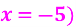
У декартовій системі координат: координата точки по осі Х (абсциса)
Графіку функції 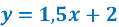належить точка (2;5)
Функція задана формулою 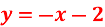. Знайдіть значення функції, якщо значення аргументу = -2 (0) НЕМА ТАКОЙ НІ У КОГО !!!
Функція задана формулою ( x-будь-яке число, окрім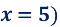
Функція задана формулою 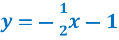. Знайдіть значення функції, якщо значення аргументу = 6 (-4) залежної змінної.
Правило, за допомогою якого за кожним значенням незалежної змінної можна знайти єдине значення залежної змінної (функція)
У декартовій системі координат: координата точки по осі У (ордината)
Графіку функції належить точка (2;-6) У ОБОИХ ОДНОВРЕМЕННО !!!

V. Вивчення нового матеріалу

З усіх питань, що підлягають вивченню з теми, на урок виносяться: означення лінійної функції та її графік (загального вигляду) та їх загальні властивості.

Викладання нового матеріалу можна провести за планом.

Приклади величин, зв'язок між якими виражається функцією, вигляду

у = kх + b( згадаємо каністру де було 8 літрів бензину і кожну хвилину вливалося ще 4 : у = 8+4х )

Означення лінійної функції.
Властивості лінійної функції (область визначення та область значень).
Графік лінійної функції загального вигляду (геометричний зміст). Зв'язок положення графіка лінійної функції із коефіцієнтами k та b. Записи, що їх виконують учні в зошитах, можуть мати вигляд:

Конспект
Лінійна функція та її графік
1. *Означення.* Функція, яку можна задати формулюю *у =* kx + b, дe k i b числа, — лінійна функція.
Приклад: у = 2х + 2 (k = 3; b = 2) у = 2х – 3 (k = 2; b = -3)
у = - х + 5 (k= -1; b = 5) у = х (k = ; b = 0) у = 3 (k = 0; b = 3)
2. Властивості лінійної функції
1) Область визначення — будь-яке число. 2) Область значень — будь-яке число.
3. Графік функції — пряма. Щоб побудувати графік, шукаємо координати будь-яких двох його точок.
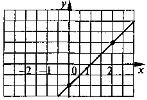
Приклад. Побудувати графік функції у = х – 1 — лінійна, отже, графіком є пряма
	х	0	2	у = х – 1
	у	-1	1
4. Властивості графіка лінійної функції
1) Якщо k > 0, то графік утворює з додатною піввіссю Ох гострий кут. 2) Якщо k < 0, то графік утворює з додатною піввіссю Ох тупий. k — кутовий коефіцієнт.
3) Число b показує ординату точки перетину графіка з віссю Оу

Оскільки повне уявлення учнів про числові множини та їх співвідношення ще не сформоване, то відповідь на питання про область визначення та область значень функції характеризуємо не зовсім «математично строгим поняттям» — будь-яке число.

VII. Засвоєння нових знань і вмінь. На цьому уроці виробляємо вміння:

розпізнавати лінійні функції та називати їх коефіцієнти;
будувати графік лінійної функції та читати його;
за формулою y = kx + b встановлювати властивості графіка.

Робота за підручником

Виконання усних вправ: № 849, 850, 851 Звернути увагу під яким кутом перетинають вісь Ох графіки функцій. В яких точках вони перетинають вісь Оу ?