Урок з теми "Площі фігур"

 

 

 

 

 

 

 

 

Урок геометрії у 9 класі

з теми:

«Площі фігур»

 

 

 

 

 

 

 

 

 

 

 

Тема уроку. «Площі фігур».

Мета уроку: формувати вміння учнів застосовувати вивчений матеріал до розв'язування задач на знаходження площ плоских фігур; розвивати пам'ять, логічне та дивергентне мислення, навички колективної та самостійної роботи; виховувати інтерес до математики, увагу, самостійність.

Тип уроку: комбінований.

Наочність і обладнання: таблиця  «Площі фігур», комп’ютерна презентація «Площі фігур» , проектор.

Хід уроку

І. Перевірка домашнього завдання

Здійснити самоперевірку за готовими розв’язаннями.

Завдання 9, №5 (б).

Дано:

ΔАВС, АС = а, А = 45°,

С = 60°.

Знайти:

S_ΔАВС.

Розв’язання:

S_ΔАВС.= АВ∙АС∙. Знайдемо АВ за теоремою синусів:

= . Оскільки = 180° - ( 45° + 60°) = 75°, то

= ,   АВ = . Тоді  S_ΔАВС =  =

= = 0,32 а².

Відповідь. 0,32 а².

Завдання 9, №6 (б)

Розв’язання:

а) р = = 16. S = = = 24.

R = = = 8, r = = = 1,5.

Відповідь. R = 8, r = 1, 5.

ІІІ. Актуалізація опорних знань..

1. Повторити теоретичний матеріал за таблицею «Площа фігур».

Запитання до класу.

1. Сформулюйте властивості площі плоских фігур.
2. Чому дорівнює площа прямокутника, якщо відомі його сторони?
3. Чому дорівнює площа прямокутника, якщо відомі діагоналі прямокутника і кут між ними?
4. Чому дорівнює площа квадрата, якщо відома:

а) сторона квадрата;

б) діагональ квадрата?

5. Чому дорівнює площа паралелограма, якщо відомі:

а) сторона паралелограма і висота, проведена до неї;

б) дві сусідні сторони паралелограма і кут між ними;

в) діагоналі й кут між ними?

6. Чому дорівнює площа ромба, якщо відомі:

а) сторона і висота ромба;

б) сторона і кут ромба;

в) діагоналі ромба?

7. Чому дорівнює площа трикутника, якщо відомі:

а) сторона трикутника і висота, проведена до неї;

б) дві сторони трикутника і кут між ними;

в) три сторони трикутника;

г) радіус вписаного кола і сторони трикутника;

д) радіус описаного кола і сторони трикутника?

8. Чому дорівнює площа:

а) прямокутного трикутника;

б) правильного трикутника?

9. Чому дорівнює площа трапеції, якщо відомі:

а) основи і висота трапеції;

б) діагоналі трапеції і кут між ними?

2. Вправа з сигнальними картками.

Презентація «Площі фігур». Н а слайдах зображені формули, відкриваючи які, формулюю твердження істинне або ні. Учні показують зелену картку, якщо твердження хибне і рожеву, якщо – істинне.

Слайди 1- 11

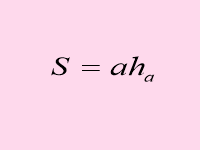
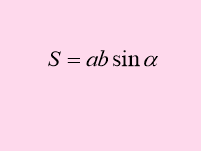
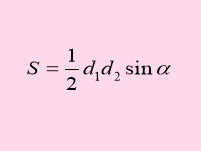
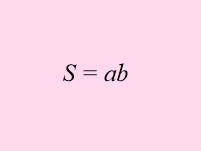
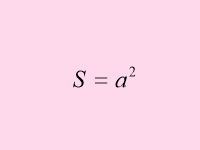
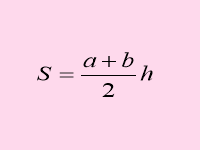
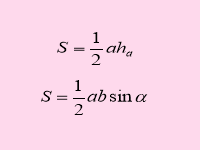
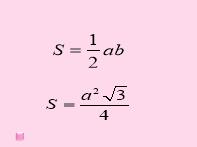
IV. Розв'язування вправ.

1.Розвязування вправ за готовими малюнками на дошці ( 1 рівень):

 

Знайдіть площі фігур.

 

 

10

                             

 

 

 

 

 

 

 

 

 

 

2.Розвязування задач ( 2 рівень)

Слайди 1 – 4.

На кожному слайді зображені фігури з відомими сторонами або кутами. Завдання: знайти площі фігур. Учні розв’язують задачі, хід розв’язання з’являється на слайді поступово.

 

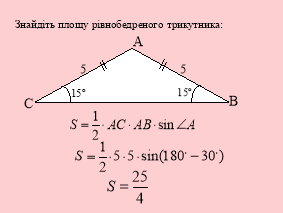
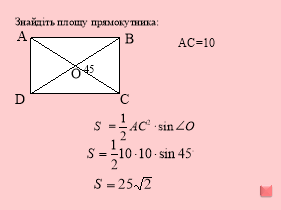
3. Розв’язування задачі кількома способами ( ІІІ рівень).

Колективна робота.

Задача. Знайти площу ромба з діагоналями 6см та 8 см.

( без застосування формули  S = d₁d₂ ).

І спосіб:

Дано: ABCD – ромб,

AC = 6 см,

BD = 8 см.

 Знайти: S_ABCD.

Розв’язання:

 Так як ABCD – ромб, то AC =BD, AO = OC; BO = OD.

 Маємо 4 рівних  прямокутних  трикутника з катетами  AO = 3 см, BO = 4 см.

 S _АОВ =AO • OB =• 3 • 4 = 6(см²).

 S_ABCD = 4 S  _AOB =   4 • 6 = 24(см2).

Відповідь: 24 см².

ІІ спосіб:

Розв'язання : так як ABCD – ромб, то AC – вісь симетрії. Отже,  ΔABC =  ΔADC.

 S_ABCD = 2 S  _ABC, S  _ABC =AC•BO,  S  _ABC =  • 6 • 4 = 12(см²⁾.

 S_ABCD = 2 • 12 см² = 24 см².

Відповідь: 24 см².

 

ІІІ спосіб.

Розв'язання : так как ABCD – ромб, то AC  перпендикулярна  BD, Δ AOB – прямокутний , тоді  за  т Пифагора AB² = AO² + BO². Отже, AB = ВС =5 см

Знайдемо площу Δ АВС за формулою Герона.

Р = = 8;  S_АВС = = 3∙4 =12 (см²).

S_ABCD = 2 • 12 см² = 24 см².

Відповідь: 24 см².

 

 

ІV. Тестова самостійна робота.

І варіант

1. Знайдіть площу прямокутника зі сторонами 3см та 5см.

А) 8см²;    Б) 16 см²;    В) 15 см²;   Г)225 см².

2. Знайдіть площу паралелограма зі стороною 5см  та проведеною до неї висотою 4см.

А) 18 см²;    Б) 9 см²;    В) 10 см²;   Г) 20 см².

3.Сторона правильного трикутника дорівнює 4см. Знайдіть його площу.

А) 16 см²;    Б) 4см²;    В) 15 см²;    Г) 20 см².

4. Знайти радіус кола, описаного навколо трикутника зі сторонами 15см, 24см. і 15см.

А) 8см²;    Б) 16 см²;    В) 15 см²;     Г)12,5 см².

 

ІІ варіант

1. Знайдіть площу  квадрата зі стороною 7см .

А)49 см²;   Б)14 см²;    В) 28 см² ;   Г) інша відповідь.

2. Знайдіть площу ромба зі стороною 10см  та  висотою 8см.

А) 80 см²;    Б) 18 см²;    В) 40 см²;  Г) 2 см².

3.Периметр правильного трикутника дорівнює 6см. Знайдіть його площу.

А) см²;      Б) 9 см²;     В) 4 см²;     Г) 24 см².

4.Знайти радіус кола, вписаного  у трикутник зі сторонами 29см, 25см і 6см.

А) 6 см²;    Б) 8 см²;    В) 4см²;     Г) 2 см².

V. Підсумок уроку.

Виконати завдання:

За 3 хвилини створити шпаргалку- пам’ятку  до теми «Площі фігур»

Учні записують у пусті клітинки відповідні формули площ.

Формули площ.

Фігура	Формула площі		Формула площі
Прямокутний трикутник		Ромб
Правильний трикутник		Квадрат
Довільний трикутник		Прямокутник
Паралелограм		Трапеція

 

VІ. Домашнє завдання

1. Підготуватися до тематичної контрольної роботи № 3.
2. Розв'язати задачі : Завдання 9, №7 (г), №10(а).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Роздатковий

матеріал

 

 

 

 

 

 

 

 

 

 

 

 

 

Домашня робота.

Розв’язання:

Завдання 9, №5 (б).

Дано:

ΔАВС, АС = а, А = 45°,

С = 60°.

Знайти:

S_ΔАВС.

Розв’язання:

S_ΔАВС.= АВ∙АС∙. Знайдемо АВ за теоремою синусів:

= . Оскільки = 180° - ( 45° + 60°) = 75°, то

= ,   АВ = . Тоді  S_ΔАВС =  =

= = 0,32 а².

Відповідь. 0,32 а².

 

Завдання 9, №6 (б)

Розв’язання:

а) р = = 16. S = = = 24.

R = = = 8, r = = = 1,5.

Відповідь. R = 8, r = 1, 5.

 

 

Прізвище___________________________

Тест:

І варіант

1. Знайдіть площу прямокутника зі сторонами 3см та 5см.

А) 8см²;    Б) 16 см²;    В) 15 см²;   Г)225 см².

2. Знайдіть площу паралелограма зі стороною 5см  та проведеною до неї висотою 4см.

А) 18 см²;    Б) 9 см²;    В) 10 см²;   Г) 20 см².

3.Сторона правильного трикутника дорівнює 4см. Знайдіть його площу.

А) 16 см²;    Б) 4см²;    В) 15 см²;    Г) 20 см².

4. Знайти радіус кола, описаного навколо трикутника зі сторонами 15см, 24см. і 15см.

А) 8см²;    Б) 16 см²;    В) 15 см²;     Г)12,5 см².

 

Прізвище___________________________

Тест:

ІІ варіант

1. Знайдіть площу  квадрата зі стороною 7см .

А)49 см²;   Б)14 см²;    В) 28 см² ;   Г) інша відповідь.

2. Знайдіть площу ромба зі стороною 10см  та  висотою 8см.

А) 80 см²;    Б) 18 см²;    В) 40 см²;  Г) 2 см².

3.Периметр правильного трикутника дорівнює 6см. Знайдіть його площу.

А) см²;      Б) 9 см²;     В) 4 см²;     Г) 24 см².

4.Знайти радіус кола, вписаного  у трикутник зі сторонами 29см, 25см і 6см.

А) 6 см²;    Б) 8 см²;    В) 4см²;     Г) 2 см².

 

 

Формули площ.

Фігура	Формула площі		Формула площі
Прямокутний трикутник		Ромб
Правильний трикутник		Квадрат
Довільний трикутник		Прямокутник
Паралелограм		Трапеція