Урок з теми"Раціональні рівняння. Рівносильні рівняння"
Тема. Раціональні рівняння. Рівносильні рівняння.
Мета. Домогтися засвоєння учнями змісту понять «раціональне рівняння», «ціле раціональне рівняння», «дробово - раціональне рівняння» та усвідомлення логічного зв’язку між цими поняттями; дати означення рівносильних рівнянь; сформувати у учнів уявлення про зміст поняття «ОДЗ рівняння», про роль цього поняття в побудові загальної схеми розв’язування дробово - раціонального рівняння та про саму схему розв’язування дробово- раціонального рівняння; виробити вміння відрізняти одне від одного вивчені види рівнянь та аргументувати власну думку, знаходити, використовуючи зміст поняття «ОДЗ рівняння», а також розв’язувати найпростіші дробово - раціональні рівняння.
Тип уроку. Урок засвоєння нових знань.
Хід уроку.
І. Організаційний етап.
ІІ. Перевірка домашнього завдання.
ІІІ. Мотивація навчальної діяльності.
- Оголошення теми та мети уроку.
- Вивченні способи перетворень раціональних виразів становлять інтерес у зв’язку з тим, що дозволяють розглянути розв’язування рівнянь, у багатьох з яких одна або обидві частини являють собою раціональний вираз. Сьогодні розглянемо один із способів розв’язування найпростіших дробово - раціональних рівнянь
ІV. Актуалізація опорних знань.
Усні вправи(умова на дошці).
-
Обчисліть: 1)
 +
+ ; 2)
; 2) 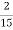 -
-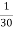 ; 3)
; 3) 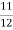 +
+ ; 4)
; 4)  ; 5) 3:
; 5) 3: ; 6)
; 6) 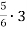 ; 7)
; 7) :
: ; 8)
; 8)  :2.
:2.
-
Укажіть допустимі значення змінної у виразі: 1)х2 – 4; 2)
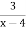 ; 3)
; 3)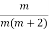 ; 4)
; 4)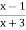 ; 5)
; 5)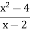 ; 6)
; 6)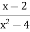 . При яких значеннях цих змінних дані вирази дорівнюють нулю?
. При яких значеннях цих змінних дані вирази дорівнюють нулю?
V. Формування знань.
План вивчення нового матеріалу.
- Означення раціонального рівняння, цілого раціонального рівняння, дробового раціонального рівняння (з прикладами).
- Означення ОДЗ раціонального рівняння. Як знайти ОДЗ раціонального рівняння.
- Алгоритм рівносильних перетворень раціонального рівняння.
- Приклад застосування вивченого алгоритму.
- Схема розв’язування найпростіших дробових раціональних рівнянь.
Опорний конспект.
1.Якщо обидві частини рівняння є раціональними виразами то дане рівняння є раціональним. Наприклад:4(х-8)=7-9х; ![]() =8;
=8; ![]() =
=![]()

2.ОДЗ рівняння - це спільна ОДЗ виразів лівої та правої частини рівняння. Наприклад:
1)4(х-8)=7-9х – ціле раціональне рівняння, тому його ОДЗ – будь – яке число;
2)![]() =8 – дробово - раціональне рівняння. Тому його ОДЗ знаходимо з умови х-4
=8 – дробово - раціональне рівняння. Тому його ОДЗ знаходимо з умови х-4![]() х
х![]() тобто ОДЗ рівняння будь – яке число, крім числа 4.
тобто ОДЗ рівняння будь – яке число, крім числа 4.
3)![]() =
=![]()
х-1![]() та х-2
та х-2![]()
х![]() х
х![]() , отже ОДЗ рівняння будь – яке число крім чисел 1 та 2.
, отже ОДЗ рівняння будь – яке число крім чисел 1 та 2.
3.Алгоритм розв’язування дробово - раціональних рівнянь.
- Знайти ОДЗ рівняння.
-
Звести його до виду
 =0 шляхом рівносильних перетворень(А і В цілі раціональні вирази).
=0 шляхом рівносильних перетворень(А і В цілі раціональні вирази).
- Замінити дане рівняння на рівняння виду А=0; розв’язати його.
- Перевірити, чи всі знайдені корені входять до ОДЗ рівняння; ті з коренів, що не входять, є сторонніми коренями.
Приклад. ![]() =0
=0
-
ОДЗ: х-2
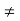 0; х
0; х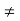 2
2
- 2х2-4х=0
|
2х(х-2)=0 2х=0 або х-2=0 х=0 або х=2 х=0 входить в ОДЗ, х=2 не входить в ОДЗ, сторонній корінь. Відповідь: о. |
Рівносильні рівняння - це рівняння, які мають ті самі корені або не мають коренів. Наприклад: рівняння 2х2-4х=0 і 2х(х-2)=0 рівносильні, а рівняння ![]() =0 і 2х(х-2)=0 не рівносильні. Рівняння
=0 і 2х(х-2)=0 не рівносильні. Рівняння ![]() =0 рівносильне системі
=0 рівносильне системі ![]()
Основні властивості рівнянь.
- Якщо в деякій частині рівняння виконати тотожні перетворення, яке не змінює ОДЗ, то одержимо рівняння рівносильне даному.
- Якщо деякий доданок перенести з однієї частини рівняння в іншу, змінивши знак на протилежний, то одержимо рівняння рівносильне даному.
- Якщо обидві частини рівняння помножити або поділити на одне й те ж саме число відмінне від нуля, то одержимо рівняння рівносильне даному.
VІ. Формування вмінь.
1.Робота з підручником.(В.Кравчук. Алгебра 8кл. 2016р.)
№197. Назвіть цілі раціональні рівняння, дробові раціональні рівняння: а)![]() =1; б)3(х-11)=0; в)
=1; б)3(х-11)=0; в)![]() – х=3; г)
– х=3; г)![]() =0
=0
№199. Чи рівносильні рівняння? а)![]() =8 і
=8 і ![]() =2; б)
=2; б)![]() =
=![]() і
і ![]() -
-![]() =0; в)
=0; в)![]() =0 і х(х+3)=0; г)
=0 і х(х+3)=0; г)![]() =
=![]() і 2х=4.
і 2х=4.
2.Робота учнів біля дошки.
Розв’язати рівняння.
№200. а)![]() =0; б)
=0; б)![]() =0; в)
=0; в)![]() =0
=0
№201. а)![]() +
+![]() =0; б)
=0; б)![]() =
=![]() ; в)
; в)![]() =
=![]() .
.
№202. а![]() +1=0; б)
+1=0; б)![]() =2; в)
=2; в)![]() =3.
=3.
VІІ. Підбиття підсумків уроку (завдання на картках).
-
Правильним розв’язком рівняння
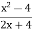 =0 є: а)х=
=0 є: а)х=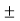 2; б)х=2, х
2; б)х=2, х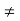 -2; в) х=-2, х
-2; в) х=-2, х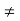 2;г)х=-2; д)х=2.
2;г)х=-2; д)х=2.
-
Установіть правильний порядок розв’язання рівняння
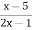 =0
=0
а). Відповідь: 5.
б) ОДЗ: 2х-1![]() 0; х
0; х![]() 0,5
0,5
в)х-5=0, х=5 – входить в ОДЗ.
VІІІ. Домашнє завдання. 1.Пункт 8 (вивчити означення раціонального рівняння, цілого раціонального рівняння, дробового раціонального рівняння, ОДЗ раціонального рівняння, алгоритм розв’язування дробового раціонального рівняння шляхом рівносильних перетворень).
2.Розвязати №204.


про публікацію авторської розробки
Додати розробку
