Урок з теми: "Рівняння"

Про матеріал

Урок- практикум з теми:"Рівняння",на якому беруть участь учні 7-11 класів.Предметна компетентність: ознайомити учнів із вченими, які заклали фундамент алгебри, як науки про рівняння, звести в систему відомості про рівняння, формувати в учнів уміння розв’язувати рівняння й використовувати ці знання й уміння для розв’язання рівнянь, що містять модуль та рівняння з параметрами.

Перегляд файлу

Розум людський володіє трьома ключами, які відкривають усе, - цифрою, буквою, нотою. Знати, думати, мріяти. Все в цьому.

В.Гюго

Тема: Рівняння

Мета: Ознайомити учнів із вченими, які заклали фундамент алгебри, як науки про рівняння, звести в систему відомості про рівняння, формувати в учнів уміння розв’язувати рівняння й використовувати ці знання й уміння для розв’язання рівнянь, що містять модуль та рівняння з параметрами.

Виховувати культуру математичних записів та вміння грамотно висловлювати думки.

Тип: Застосування знань, умінь та навичок.

Вид: Урок-практикум

Учні повинні знати: означення рівняння, що таке корінь рівняння, що значить розв’язати рівняння, означення лінійного рівняння, квадратного рівняння, від чого залежить кількість коренів рівняння, що таке параметр, модуль та його властивості;

уміти: розв’язувати лінійні рівняння, квадратні найпростіші рівняння, що містять модуль та параметри, розкладати многочлени на множники, користуватися формулами скороченого множення;

цінувати: почуття впевненості в собі, вміння самовиражатися, допитливість, глибину засвоєння інформації, уміти бачити істотне й другорядне в об’єкті, свідоме ставлення до своєї діяльності, прагнення до досконалості.

Хід уроку

І. Організаційний момент.

1) Перевірка робочого місця.

2) Виконання правил спілкування:

дотримання правил поведінки в кабінеті;
осмислення вимог вчителя;
говорити має хтось один;
говорити необхідно по суті, цінувати кожну хвилину уроку;
вчитися поважати думку іншого.

3) Вступна бесіда.

Сьогодні ми будемо вести розмову про рівняння, їх види та розв’язувати їх, що є однією із складових частин алгебри, бо алгебра виникла як наука про розв’язання рівнянь. У 825 році арабський учений Мухаммед аль-Хорезмі написав книгу "Кітаб аль-джебр ал-Мукабала", що означає "Книга про відновлення і протиставлення", в якій алгебра розглядається як самостійна складова математики. Це був перший у світі підручник з алгебри. Саме слово "алгебра" походить від слова "аль-джебр", що означає перенесення від’ємних доданків із однієї частини рівняння в другу зі зміною знака.

Пам’ятки стародавньої культури Єгипту свідчать, що вже 4 тисячі років тому деякі задачі розв’язували за допомогою рівнянь. Правда, робили це дещо інакше, ніж тепер, оскільки в ті часи не було навіть буквеної символіки, і все записували словами.

Великий грецький математик Діофант (ІІІ ст. н.е.) багато зробив для розвитку математики. Він увів деякі буквені позначення, щоб полегшити розв’язування рівнянь. Діофант ставив коефіцієнт не перед змінною, як це робимо ми, а після змінної.

Рівняння допомагають розшифрувати деякі історичні факти. Так розшифрована біографія старогрецького ученого математика Діофанта (жив 23 століття тому), про якого відомо мало. Дещо про його життя і про те, скільки років він прожив, можна судити із запису, зробленого на його могильній плиті:

Прах Діофанта гробниця ховає, вдивися – і камінь

Мудрим мистецтвом розкриє покійного вік:

З волі богів шосту частину життя був він дитина,

А ще половину шостої – стрів із пушком на щоках.

Тільки минула сьома, з коханою він одружився,

З нею п'ять років прожив, і сина діждався мудрець.

Та півжиття свого тішився батько лиш сином:

Рано могила дитину у батька забрала.

Років двічі по два батько оплакував сина.

А по роках цих сам стрів він кінець свій печальний…

Скільки ж років жив Діофант?

Для відповіді на це запитання потрібно скласти рівняння, в якому позначити через х – кількість років життя математика.

Отже,

1 _х ₊1 _{х +} 1 _{х +} 5 ₊ 1 _{х +} 4 = х

6 12 7 2

Легко підрахувати, що Діофант прожив 84 роки, але коли точно – невідомо. Час (ІІ – ІІІ ст. н.е.) його життя визначено з непрямих міркувань.

У подальший розвиток алгебри зробили великий внесок європейські вчені Франсуа Вієт (1540 – 1603) і Рене Декарт (1596 – 1650), які ввели в алгебру букви й розробили правила дій з буквеними виразами.

4) Повідомлення про оцінювання.

Ваша оцінка за урок формуватиметься вами самими. Кожне завдання буде мати визначену кількість балів. Оцінку 12 балів отримає той, хто за урок набере максимальну кількість балів, а далі 11 тощо.

5) Повідомлення про роботу на уроці.

Кожен учень працює в своїй віковій групі, де за їх роботою стежать вчитель, гості семінару, які можуть допомогти, якщо виникли ускладнення при розв’язанні вправ, консультант групи та секретар.

На столі в кожній групі лежать аркуші із завданнями, рефлексія, яку заповнюють після кожного етапу уроку і виставляють бали за розв’язані завдання.

Рефлексія

Прізвище	Початкова		Проміжна			Кінцева	Підсум-кова
	Діагно- стична рефлексія	Само-стійна робота	Ще треба вчитися		Я вже вмію	Само-стійна робота
			Зелений	Жовтий	Червоний
			1-6 б.	7-9 б.	10-12 б.

ІІ. Актуалізація опорних знань, умінь та чуттєвого досвіду.

Єдиний шлях, який веде до знань – це діяльність.

Б.Шоу

З цим не можна не погодитись, бо "Потрібно багато вчитися для того, щоб дещо знати" (Ш.Монтескьє), "А у навчанні не можна зупинятися" (Сюнь-Цзі).

Ось чому сьогодні на уроці ми особливу увагу приділимо рівнянням, що містять модуль та рівнянням з параметрами, які розглядаються в шкільному курсі алгебри.

- Фронтальна бесіда і складання "Асоціативного куща", як одного із різновидів мозкового штурму по темі "Рівняння".

1) Що називається рівнянням?

2) Що називається коренем рівняння?

3) Що значить розв’язати рівняння?

4) Які використовуємо властивості рівнянь?

5) Замінивши одне рівняння іншим за допомогою цих властивостей, які ми одержуємо рівняння? (рівносильні)

6) З якими видами рівнянь ви вже знайомі?

Асоціативний кущ

Повторимо алгоритми розв’язку деяких із них (по готовим таблицям), де особливу увагу приділимо визначенню кількості коренів кожного виду рівнянь.

Лінійні	Дробово-раціональні	Квадратні

Проведемо рефлексію "Як я оцінюю свої знання по даній темі?" (Кожен учень заповнює початкову діагностичну рефлексію, а після виконання самостійної роботи заповнює другу частину початкової рефлексії).

Правильні відповіді в завданнях дозволять вам прочитати зашифроване речення. ("Бажаємо успіху!")

7 клас

1. 2х – 3 = 5

А) 1 Б) 8 В) 0 Г) 4

2. 5х + 7 = 4х + 9

А) 5 Б) 2 В) 1 Г) 0

3. х + 2 = - 3

А) -5 Б) -1 В) коренів немає Г)-5 і -1

8 клас

1. 2х – 1,2 = 4,8

А) 2 Б) 3 В) 0 Г) 6

2. 5х – 3 (х + 1) = 1 + х

А) 2 Б) -4 В) 4 Г) 0

3. 4 - х = - 2

А) -6 Б) 2 В) -6 і 2 Г) коренів немає

4. При якому значенні а рівняння має корінь

ах + 2 = 6

4х + 2 = 6

4х = 4

а = 1

А) 1 Б) -2 В) 3 Г) -1

(а – 3)х = 4

(а - 3)2 = 4

а – 3 = 2

а = 5

А) 5 Б) 3 В) 1 Г) -5

5. х - 5 = 0

А) -5 Б) 5 В) 3 Г) 0

5. 2х + 6 = 0

А) 3 Б) 0 В) -3 Г) 6

6. Розв’язати рівняння

х - 4 = 5

3х - 4 = 2

х – 4 = 5

х = 9

х – 4 = - 5

х = - 1

3х – 4 = 2

3х = 6

х = 2

3х – 4 = - 2

3х = 2

_{х =} 2

Відповідь: -1; 9

Відповідь: 2 ; 2

7. ах = 2

^{а = 0} ^а^⁰

0х = 2 _{х =} 2

коренів немає

Відповідь: 1. коренів немає, якщо а = 0

2. 2 , якщо а  0

^{Х =} а

(а – 2) х = 5

^{а – 2 = 0} ^{а – 2}^⁰

а = 2 а  2

0х = 5 _{х =} 5

коренів немає а – 2

Відповідь: 1. коренів немає, якщо а = 2

2. _{х =} 5 , якщо а  2

а - 2

9 клас

1. – 2 х² = 0

А) - 2 Б) 0 В) 1 Г) 2

2. х² – 4х = 0

А) 0 Б) 4 В) 0 і 4 Г) - 4 і 0

3. х² – 4х + 3 = 0

А) 1 Б) -1 і - 3 В) 3 Г) 1 і 3

11 клас

1. х² – 7х + 12 = 0

А) 0 Б) 3; 1 В) 3; 4 Г) 2

2. х² – 5х + 6

х – 3 ^{= 0}

А) 3; 2 Б) 3 В) 2 Г) 0; 1

3. х^{2 –}5х + 6 = - 3

А) 1; 2 Б) немає коренів В) 7; 0 Г) - 3

4. 3х + 2 = - 4

А) немає коренів Б) - 2 В) 2/3 Г) 0

4. 3 + х - 2 = 3

А) 2; - 2 Б) 2 В) - 2 Г) 0

5. При якому значенні а рівняння має корінь

ах – 3 = 5 - х

А) 0 Б) 3 В) - 3 Г) 1

а²х²+ 2 ах + 1 = 0

А) 2 Б) 3 В) - 4 Г) - 1

6. Розв’язати рівняння

2х - 6 = х

2 х² + 1 - 1 = 3

2 х² + 1 = 4

х² + 1 = 2

2х – 6 = - х

3х = 6

х = 2

2х – 6 = х

х = 6

х² + 1 = -2

х²= - 3

коренів немає

х² + 1 = 2

х² = 1

х =  1

Відповідь: 2; 6

Відповідь: - 1; 1

7. ах – 3 = 1 – 2х

ах + 2х = 3 + 1

х(а + 2) = 4

7. ах – а² = 3х – 9

ах – 3х = а² – 9

х (а – 3) = а² – 9

а + 2 = 0

а = - 2

а + 2  0

а  - 2

а – 3 = 0

а = 3

а – 3  0

а  3

0х = 4

коренів немає

_{х =} 4

а + 2

0х = 0

х – будь-яке число

_{х =} а² – 9 ₌а + 3

а – 3

Відповідь: 1. немає коренів, якщо а = -2

2. _{х =} 4 , якщо а  - 2

а + 2

Відповідь: 1. х – будь-яке число, якщо а = 3

2. х = а + 3, якщо а  3

Проводимо самоперевірку. За 1 – 5 – по 1 балу, 6,7 – по 3 бали.

	№1	№2	№3	№4	№5	№6	№7
7 клас	Г) 4	Б) 2	В) коренів немає	А) 1	Б) 5	- 1; 9	1) х ₌ 2 , а  0 а 2) немає коренів, а = 0
8 клас	Б) 3	В) 4	Г) коренів немає	А) 5	В) – 3	2; 2 3	1) х ₌ 5 , а  0 а - 2 2) немає коренів, а = 2
9 клас	Б) 0	В) 0; 4	Г) 1 і 3	А) немає коренів	Б) 3	2; 6	1) х ₌ 3 , а-2 а + 2 2) немає коренів, а = - 2
11 клас	В) 3; 4	В) 2	Б) немає коренів	Б) 2	Г) - 1	- 1; 1	1) х – будь-яке число, якщо а = 3 2) х = а + 3, якщо а  3
Вислів	"Ба	Жа	є	мо	ус	пі	ху!"

ІІІ. Застосування знань, формування умінь та навичок.

Набагато складніше побачити проблему, ніж розв’язати її. Для першого потрібна творча уява, а для другого лише вміння.

Д.Бернал

1. Чи дійсно це так, ми побачимо на практиці при розв’язуванні рівнянь, що містять модуль. Для цього повторимо все про модуль (робота з таблицею).

Розв’язування раціональних рівнянь, що містять модуль

2. Звертається увага на розв’язок рівнянь, що містять модуль, із завдань самостійної роботи.

7 клас	8 клас
а)х – 5 = 0, х – 5 = 0, х = 5 б)х + 2 = - 3, коренів немає в)х – 4 = 5, 1) х – 4 = - 5 2) х – 4 = 5 х = - 1 х = 9	а)2х + 6 = 0, 2х + 6 = 0, х = - 3 б)4 – х = - 2 , коренів немає в)3х – 4 = 2 1) 3х – 4 = - 2 2) 3х – 4 = 2 3х = 2 3х = 6 х = 2/3 х = 2
9 клас	11 клас
а)3х + 2 = - 4, коренів немає б)2х – 6 = х 1) 2х – 6 = - х 2) 2х – 6 = х 3х = 6 х = 6 х = 2	а)х² – 5х + 6 = - 3, коренів немає б)2х² + 1- 1 = 3, 2х² + 1 = 4, х² + 1= 2 1) х² + 1 = - 2 2) х² + 1 = 2 х² = - 3 х²= 1 коренів немає х = -1 або х = 1

При розв’язуванні цих рівнянь використано властивості модуля. Вчитель звертає увагу на кількість коренів рівнянь в залежності від значення модуля.

3. Розв’язати рівняння, використовуючи властивості модуля, коли модуль задано неявно.

7 клас

8 клас

2х - 3 = 1

2х = 4

х = 2

х = -2 або х = 2

Відповідь: -2; 2

6 + х + 2 = 3

х + 2 = 3 - 6

х + 2 = - 3

Коренів немає, так як -3  0

Відповідь: немає коренів

9 клас

11 клас

х²– 4х - 6 = х

х²– 4х = х + 6

х² – 4х = -х – 6 х² – 4х = х + 6

х² + 5х + 6 = 0 х² – 5х – 6 = 0

х = -2 або х = -3 х = 6 або х = - 1

Відповідь: - 3; - 2; - 1; 6

х²- 3х - 4 = 0

х = а, а  0

а²– 3а - 4 = 0

а = 4 або а = - 1 – не підходить

х = 4

х = - 4 або х = 4

Відповідь: - 4; 4

Розв’язування рівнянь методом інтервалів та методом граф

7 клас

8 клас

х- 3= 4

х + 1 - 5 = 2

х - 3 = - 4

х = - 1

Коренів немає,

так як - 1 0

х - 3 = 4

х = 7

х = - 7 або х = 7

х + 1 - 5 = - 2 х + 1 - 5 = 2

х + 1 = 3 х + 1 = 7

х + 1 = - 3 х + 1 = 3 х + 1 = - 7 х + 1 = 7

х = - 4 х = 2 х = - 8 х = 6

Відповідь: - 8; - 4; 2; 6

Відповідь: - 7; 7

9 клас

11 клас

х + 1= х - 2

х + 1- х - 2= 0

1. Знаходимо нулі підмодульних виразів.

х + 1 = 0 х – 2 = 0

х = - 1 х = 2

- 1 2

2. х  - 1

- (х + 1) + (х – 2) = 0

- х – 1 + х – 2 = 0

0х = 3

Коренів немає

3. – 1 < х < 2

х + 1 + х – 2 = 0

2х = 1

х = 0,5 – корінь

4. х  2

х + 1 – х +2 = 0

0х = - 3

Коренів немає

Відповідь: 0,5

х - 2 + х + 3 = 5

1. Знаходимо нулі підмодульних виразів.

х – 2 = 0 х + 3 = 0

х = 2 х = - 3

- 3 2

2. х  - 3

- (х - 2) - (х + 3) = 5

- х + 2 – х – 3 = 5

- 2х = 6

х = - 3 – корінь

3. – 3 < х < 2

- (х – 2) + х + 3 = 5

- х + 2 + х + 3 = 5

0х = 0

х – будь-яке число із проміжку (- 3; 2)

4. х  2

х – 2 + х + 3 = 5

2х = 4

х = 2 – корінь

Відповідь: х  [- 3;2]

Підсумок: як бачимо, при розв’язуванні рівнянь, що містять модулі, були застосовані такі способи розв’язування рівнянь:

за означенням модуля;
метод граф;
метод інтервалів.

ІV. Розв’язування рівнянь з параметрами.

Пізнання починається зі здивування.

Аристотель

Важко не погодитися з Аристотелем при розв’язанні рівнянь з параметрами.

Вступне слово.

Оскільки на зовнішньому незалежному оцінюванні та підсумкових атестаціях усе частіше пропонується розв’язати завдання з параметрами, то, в очевидно, треба вчитися володіти прийомами їх розв’язування.

Як ви знаєте, параметр (від грецького – той, що відміряє) – величина, значення якої слугують для встановлення відмінності між елементами деякої множини. Якщо в рівняння, крім невідомих величин входять числа, що позначені буквами, які не вказані, але вважаються відомими та заданими на деякій числовій множині, то вони називаються параметрами.

Розв’язання любого рівняння можна проводити як розв’язання звичайного рівняння без параметра до тих пір, поки кожне перетворення, необхідне для розв’язку, можна виконувати однозначно. Якщо ж таке перетворення виконати неможливо, тоді розв’язок треба розбити на стільки способів, щоб в кожному із них відповідь можна було записати однозначно. Розв’язання вправ із параметрами полягає у побудові алгоритму, що дозволяє для будь-якого значення параметра знаходити відповідну множину коренів. Важливим в розв’язання рівнянь з параметрами є запис відповіді, яку потрібно записувати, розглядаючи всі можливі значення параметру і впевнитися, що всі значення параметра враховано.

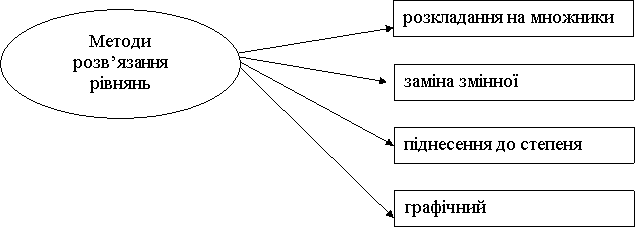
Існують такі методи розв'язання рівнянь в шкільному курсі математики.

Розглянемо застосування деяких із них при розв'язуванні вправ, а для цього переглянемо розв’язки рівнянь із самостійної роботи.

7 клас

8 клас

7. ах = 2

^{а = 0} ^а^⁰

0х = 2 _{х =} 2

коренів немає

Відповідь: 1. коренів немає, якщо а = 0

2. 2 , якщо а  0

^{Х =} а

(а – 2) х = 5

^{а – 2 = 0} ^{а – 2}^⁰

а = 2 а  2

0х = 5 _{х =} 5

коренів немає а – 2

Відповідь: 1. коренів немає, якщо а = 2

2. _{х =} 5 , якщо а  2

а – 2

9 клас

11 клас

7. ах – 3 = 1 – 2х

ах + 2х = 3 + 1

х(а + 2) = 4

7. ах – а² = 3х – 9

ах – 3х = а² – 9

х (а – 3) = а² – 9

а + 2 = 0

а = - 2

а + 2  0

а  - 2

а – 3 = 0

а = 3

а – 3  0

а  3

0х = 4

коренів немає

_{х =} 4

а + 2

0х = 0

х – будь-яке число

_{х =} а² – 9 ₌а + 3

а – 3

Відповідь: 1. немає коренів, якщо а = -2

2. _{х =} 4 , якщо а  - 2

а + 2

Відповідь: 1. х – будь-яке число, якщо а = 3

2. х = а + 3, якщо а  3

Як бачимо, розв’язання рівнянь із параметрами полягає у побудові алгоритму, який будемо складати, розв’язавши рівняння таких видів.

7 клас

8 клас

1. Для кожного значення а розв’яжіть рівняння

ах – 2 = 2х + 3

ах – 2х = 5

х (а – 2) = 5

а – 2 = 0 а – 2  0

а = 2 а  2

0х = 5 _{х =} 5

Коренів немає а – 2

Відповідь: 1. немає коренів, якщо а = 2

2. _{х =} 5 , якщо а  2

а - 2

ах + 12а = а² + 6х + 36

ах – 6х = а² – 12а + 36

х(а – 6) = а² – 12а + 36

а – 6 = 0 а – 6  0

а = 6 а  6

0х = 0 _{х =} а² – 12а + 36 ₌ а – 6

х – будь-яке а – 6

число

Відповідь: 1. х – будь-яке число, якщо а = 6

2. х = а – 6, якщо а  6

2. При яких натуральних значеннях а корінь рівняння (а + 2)х = 7 є натуральним числом

(а + 2)х = 7

а + 2 = 0 а + 2  0

а = - 2 а  - 2

0х = 7 _{х =} 7

Коренів немає а + 2

Вираз 7 набуває натуральних

а + 2 значень, якщо (а + 2) є натуральними дільниками числа 7. Так як 7 просте число, то його дільники 1 і 7.

1. а + 2 = 1 2. а + 2 = 7

а = - 1 а = 5

Так як, - 1 - ціле число, а 5 натуральне число, то розв’язком є число 5.

Відповідь: 5

2. При яких цілих значеннях а коренем рівняння є ціле число (а – 1)х = 5

(а – 1)х = 5

а – 1 = 0 а – 1  0

а = 1 а  1

0х = 5 _{х =} 5

Коренів немає а - 1

Вираз 5 набуває цілих значень, якщо

а – 1 (а – 1) є цілими дільниками числа 5. Так як, 5 просте число, то його дільниками є – 5; -1; 1; 5.

1. а – 1 = - 5 2. а – 1 = - 1

а = - 4 а = 0

3. а – 1 = 1 4. а – 1 = 5

а = 2 а = 6

Числа – 4; 0; 2; 6 – цілі, тому вони задовольняють умову завдання.

Відповідь: – 4; 0; 2; 6

3. х - 1 ₌ ах + 3

2 4

3. а _- 3 ₌ 2а + 7 х – 2  0, х + 20

х - 2 х + 2 х² – 4 х  2 х  - 2

Зводимо дроби до спільного знаменника

4 х² – 4

2 (х – 1) = ах + 3

2х – 2 = ах + 3

2х – ах = 5

х(2 – а) = 5

2 – а = 0 2 – а  0

а = 2 а  2

0х = 5 _{х =} 5

Коренів немає 2 – а

Відповідь: 1. немає коренів, якщо а = 2

2. _{х =} 5 , якщо а  2

2 – а

а(х + 2) – 3 (х – 2) = 2а + 7

ах + 2а – 3х + 6 = 2а + 7

ах – 3х = 2а + 7 – 2а – 6

х(а – 3) = 1

а – 3 = 0 а – 3  0

а = 3 а  3

0х = 1 _{х =} 1

Коренів немає а - 3

Так як, х   2, то знайдемо значення а при яких виконується ця умова.

1 1

а – 3 ^{= - 2} а – 3 ^{= 2}

1= - 2а + 6 1 = 2а – 6

2а = 5 2а = 7

а = 2,5 а = 3,5

Відповідь: 1. немає коренів, якщо а = 2,5; 3; 3,5

2. _{х =} 1 , якщо а  3

а – 3

9 клас

11 клас

1. Розв’язати рівняння х² – 6х + а = 0 при всіх значеннях параметра а.

1) Рівняння має два різних кореня, якщо дискримінант додатнє число.

Знаходимо Д = 36 – 4а

Складаємо нерівність 36 – 4а  0

- 4а  - 36

а < 9

х_1,2 = 3   9 – а

2) Рівняння має один корінь, якщо Д = 0

36 – 4а = 0

а = 9

х = 3

3) Рівняння немає коренів, якщо Д < 0

36 – 4а < 0

а  9

Відповідь: 1) х_1,2 = 3   9 – а, якщо а < 9

2) х = 3, якщо а = 9

3) немає коренів, якщо а  9

1. ах²+ 6х + 9 = 0

а = 0 а  0

6х + 9 = 0 ах²+ 6х + 9 = 0

6х = - 9 Д = 36 – 36а

х = - 1,5 1) Д  0, два різних кореня

36 – 36а  0

- 36а  - 36

а  1

х_{1,2 =} - 6  36 – 36а ₌

2а

= - 3  3 1 – а

2) Д = 0,один корінь 3) Д  0, коренів немає

36 – 36а = 0 36 – 36а < 0

- 36а = - 36 - 36а < - 36

а = 1 а  1

_{х =} - 3 , х = - 3

Відповідь: 1) х = - 1,5, якщо а = 0

2) х_1,2 ₌ - 3  3  1 – а , якщо а < 1

3) х = - 3, якщо а = 1

4) немає коренів, якщо а  1

2. Один із коренів рівняння дорівнює -3. Знайти р та другий корінь рівняння х² + рх + 6 = 0

Рівняння зведене, то за теоремою Вієта х₁ + х₂ = - р

х₁ х_{2 =}6

так як х₁ = - 3, маємо

- 3 + х₂ = р -3 – 2 = р р = - 5

- зх₂ = 6 х₂= -2 х₂ = -2

Відповідь: р = - 5; х₂= - 2

2. а (х – а) _{= 0}х –3  0

х - 3 х  3

1) а(х – а) = 0 2) а = 3

а = 0 а  0 3(х–3) ₌ 0

0х = 0 х – а = 0 х – 3

х – будь-яке х = а, 3 = 0 – невірно,

число, х  3 коренів немає

Відповідь: 1) х – будь-яке число, крім х = 3, якщо а = 0

2) х = а, якщо а  0, а  3

3) коренів немає, якщо а = 3

3. х ₊ х ₌ 4а² – 1 а  0

а - 1 а а(а – 1) а  1

ах + х(а – 1) = 4а² – 1

ах + ах – х = 4а² – 1

2ах – х = 4а² – 1

х(2а – 1) = 4а² – 1

2а – 1 = 0 2а – 1  0

а = 0,5 а  0,5

0х = 0 х ₌ 4а² – 1 ₌ 2а + 1

х – будь-яке число 2а - 1

Відповідь: 1. х – будь-яке число, якщо а = 0,5

2. х = 2а + 1, якщо а  0; 0,5; 1

3. немає коренів, якщо а = 0, а = 1

3. 4 _- 2 ₌ ах² + 15 х  - 5

х – 5 х + 5 х² – 25 х  5

4(х + 5) – 2 (х – 5) = ах² + 15

4х + 20 – 2х + 10 = ах² + 15

ах² – 2х – 15 = 0

а = 0 а  0

- 2х – 15 = 0 ах² – 2х – 15 = 0

- 2х = 15 Д = 4 + 60а = 4(1 + 15а)

х = - 7,5 х_1,2 ₌ 2   4(1 + 15а) ₌

2а

₌ 1   1 + 15а

1) Д  0 2) Д = 0 3) Д  0

1 + 15а  0 1 + 15а = 0 1 + 15а  0

а _ _- 1 а _{= -} 1 а __- 1

15 15 15

х_1,2 ₌ 1  1 + 15а х ₌ 1 коренів немає

а а

Відповідь: 1. х = - 7,5, якщо а = о

2. х_1,2 ₌ 1  1 + 15а , якщо а  _- 1 , а  0

а 15

3. х ₌ 1, якщо а ₌ _- 1 , а  0

а 15

4. немає коренів, якщо а __- 1 , а  0, а = 5

На основі розв’язаних вправ, складемо алгоритми розв’язку лінійних та квадратних рівнянь з параметрами.

Лінійні рівняння

Квадратні рівняння

ах + в = 0

ах = - в

ах² + вх + с = 0

а = 0 а  0

Проводимо проміжну рефлексію.

Перейдемо до графічного розв’язування рівнянь з параметрами. Для цього розглянемо рекомендацію "Графічні методи розв’язування рівнянь з параметрами".

Графічні методи розв’язування рівнянь з параметрами

Для кожного значення а визначити кількість коренів рівняння.

І. х – 2 = а

Запишемо ліву та праву частину рівняння у вигляді функції

у = х – 2 і у = а

Побудуємо графіки функції в одній системі координат

а) у = х – 2 – лінійна функція, областю визначення функції є всі дійсні числа. Графіком є пряма, яка проходить через точки (0; - 2) і (2; 0).

б) у = а. Графіком є пряма, паралельна осі ох.

В залежності від параметра а рівняння має один корінь: х = а + 2

ІІ. х - 2 = а

Запишемо ліву та праву частину рівняння у вигляді функції

у = х – 2 і у = а

Побудуємо графіки функції в одній системі координат

Від’ємну частину графіка симетрично відображаємо відносно осі ох.

б) у = а. Графіком є пряма, паралельна осі ох.

В залежності від параметра а рівняння має таку кількість коренів:

1) немає коренів, якщо а < 0

2) один корінь, якщо а = 0

3) два корені, якщо а  0

ІІІ. х² – 6х + 7 = а

Запишемо ліву та праву частину рівняння у вигляді функції

у = х² – 6х + 7 і у = а

Побудуємо графіки функції в одній системі координат

а) у = х² – 6х + 7 – квадратична функція, областю визначення функції є всі дійсні числа. Графіком є парабола, вітки якої направлені вверх. Знайдемо координати вершини.

Виділяємо повний квадрат.

у = х² – 6х + 7 = (х² – 2х3 + 9) – 9 + 7 = (х – 3)² – 2

( 3; - 2) – координати вершини параболи

Будуємо параболу у = х² з вершиною в точці ( 3; - 2)

б) у = а. Графіком є пряма, паралельна осі ох.

В залежності від параметра а рівняння має таку кількість коренів:

1. немає коренів, якщо а  - 2

2. один корінь, якщо а = - 2

3. два кореня, якщо а  - 2

ІV. х² – 6х + 7 = а

Спочатку будуємо графік функції у = х² – 6х + 7, потім від’ємну частину графіка симетрично відображаємо відносно осі ох. Одержуємо графік функції у = х² – 6х + 7

Будуємо пряму у = а.

В залежності від параметра а рівняння має таку кількість коренів: