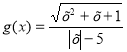Урок з теми "Розв'язування вправ на знаходження області визначення та множини значень функції"
Тема уроку:
Розв’язування вправ
на знаходження області визначення та множини значень функції
Мета уроку:
- дидактична: повторити, систематизувати, узагальнити знання учнів про функцію,її область визначення й множину значень;
- розвиваюча: розвивати в учнів логічне мислення, процеси аналізу і синтезу;
- виховна: виховувати наполегливість і почуття своєї вагомості в колективі, любов до математики
Обладнання: мультимедійний проектор, дошка, роздаткові картки
Тип уроку: закріплення вивченого матеріалу
Методи і прийоми: «Робота в малих групах», усне опитування, «Мікрофон»
Очікувані результати: після уроку учні зможуть:
• дати означення:
- функція,
- числова функція;
- значення функції в точці;
- область визначення функції;
- множина значень функції.
• розв’язувати задачі на знаходження області визначення та множини значень функцій.
Хід уроку
І Організаційний момент (3 хв.)
Вступне слово.
- Добрий день. Сідайте, будь ласка. Поки ви готуєтесь до уроку, налаштовуєтесь на роботу, я відмічу відсутніх. Чергові будь ласка, перевірте готовність дошки до роботи.
- Тема нашого уроку «Розв’язування вправ на знаходження області визначення та множини значень функції)». Мета уроку: закріпити знання учнів при розв’язуванні задач на знаходження області визначення та множини значень функції.
Після уроку ви зможете:
• дати означення:
- функція,
- числова функція;
- значення функції в точці;
- область визначення функції;
- множина значень функції.
• розв’язувати задачі на знаходження області визначення та множини значень функцій.
- І першим етапом уроку буде перевірки домашнього завдання.
ІІ Перевірка домашнього завдання (5 хв.)
- Домашнім завданням було:
|
Домашнє завдання |
• означення:
Знайти область визначення функції: а) у=х+3 б) у=4-х2
в*)
г*) |
- Теоретичну частину ми перевіримо через декілька хвилин.
- Для перевірки письмового завдання обміняйтесь, будь ласка, зошитом з сусідом за партою. Ваше завдання: перевірити наявність та правильність виконання задач. Даю вам 3 хвилини. Увага на дошку.
|
Розв’язання домашніх вправ |
|
Вправа а) для функції у=х+3 ОДЗ: х є R б) для функції у=4-х2 ОДЗ: х є R
в*) для функції х1= -4, х2=-2. Отже х є (-∞; -4)Ụ(-2;∞)
г*) для функції х≠-3. Отже, х є (-∞; -3)Ụ(-3;∞) |
- Які є запитання щодо розв’язків задач домашнього завдання?
ІІІ Актуалізація вивченого матеріалу (7 хв.)
- Наступним етапом уроку буде перевірка теоретичних знань. Я буду задавати питання, а бажаючі будуть відповідати.
Усне опитування:
1) Що називається функцією?
2) Що називається числовою функцією?
3) Як називаються змінні х та у?
4) Що називається значенням функції в точці х0?
5) Як позначається функція?
6) Що називається областю визначення функції?
- Ваші відповіді говорять про те, що теоретичний матеріал кожен з вас знає на достатньому рівні. А зараз перевіримо, наскільки добре ви вмієте розв’язувати задачі, працюючи в невеликих групах.
ІV Закріплення та осмислення вивченого матеріалу (13 хв.)
«Робота в малих групах»
- У кожного з вас на парті лежить невеликий кольоровий папірець (всього 4 кольори). Таким чином з усіх учнів ми утворюємо «4 малі групи».
- Будь ласка, пересядьте кожен в свою групу: червоний колір, жовтий колір, синій колір, зелений колір.
- Перед тим, як кожна група отримає завдання, пригадайте, як працювати в «малих групах» (див. пам’ятку) і розподіліть ролі.
- Увага! Кожна група отримує картку із завданням. На виконання завдання відводиться 5 хвилин.
|
Картка № 1 |
|
1. Знайти значення аргументу, при якому значення функції у=10-2х дорівнює 2. 2. Знайти значення функції f(х)= х-6 в точках 3; 0; - ½ .
3*. Знайти область визначення функції |
|
Картка № 2 |
|
1. Знайти значення аргументу, при якому значення функції у=10-2х дорівнює 4. 2. Знайти значення функції f(х)= 2х+6 в точках 3; 0; - ½ .
3*. Знайти область визначення функції |
|
Картка № 3 |
|
1. Знайти значення аргументу, при якому значення функції у=10-2х дорівнює 6. 2. Знайти значення функції f(х)= х-3 в точках 3; 0; - ½ .
3*. Знайти область визначення функції |
|
Картка № 4 |
|
1. Знайти значення аргументу, при якому значення функції у=10-2х дорівнює 3. 2. Знайти значення функції f(х)= х+5 в точках 3; 0; - ½ .
3*. Знайти область визначення функції |
- Час вичерпаний. Запрошую до дошки доповідача.
- Поясни, будь ласка, як ваша група розв’язувала задачі?
- Так як задачі для всіх груп були аналогічними, прошу вас перевірити свої розв’язки. Увага на дошку!
|
Відповіді до карток |
|
|
Картка № 2
f(0)=2∙0+6=6, f(-1/2)=2∙(-1/2)+6=5.
ОДЗ: х є R,крім -х2+4≠0 , х≠2 Отже, х є (-∞; 2)Ụ(2;∞)
|
Картка № 1 1. х=4 2. 0; 4; 2 3. х є (-∞;2)Ụ(2;∞) |
|
Картка № 3 1. х=2 2. 0; -3; -7/2 3. х є (-∞;4)Ụ(4;∞) |
|
|
Картка № 4 1. х=3,5 2. 8; 5; 9/2 3. х є (-∞; -3)Ụ(-3;∞) |
|
- Чи є такі групи, які отримали неправильну відповідь?
Колективна робота (10 хв.)
Слово вчителя:
- Встановлюючи область визначення функції, вказують усі значення, яких може набувати аргумент. Якщо функцію задано формулою, а про її область визначення нічого не сказано, то розуміють, що вона така сама, як і область допустимих значень змінної, яка входить до цієї формули.
- Давайте пригадаємо:
|
Функція |
Область визначення функції |
|
(многочлен п-го степеня) |
х є R |
|
g(x)≠0 |
|
|
f(x)≥0 |
- Якщо функцію задано графічно, то область визначення функції – проекція її графіка на вісь х; область значень функції – проекція її графіка на вісь у.
- Наступну задачу будемо розв’язувати письмово
Задача. Знайти область визначення функції:
а) ![]() б*)
б*) ![]()
Розв’язання
а) D(у): ![]()
![]() Отже , х є (-∞;4)Ụ(4;12]
Отже , х є (-∞;4)Ụ(4;12]
б) D(у): 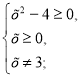
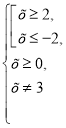 Отже, х є [2;3) Ụ (3;∞)
Отже, х є [2;3) Ụ (3;∞)
Задача: Знайти множину значень функції:
а) ![]() б*)
б*) ![]() в*)
в*) ![]()
Розв’язання
а) E(g)=(-∞; +∞)
б*) Е(у)=[10; ∞)
в*) Найменшого значення функція набуває при х0=6/2=3; у0=9-18+5=-4. Отже Е(у)=[-4; ∞)
V Підбиття підсумків, оцінювання результатів уроку (5 хв.)
«Мікрофон»
- Чи була корисною сьогоднішня робота і чого ви навчилися?
- Чи досягли ми очікуваних результатів?
- Які труднощі виникли у вас на уроці?
- А зараз будемо оцінювати роботу кожного учня на уроці (виставлення оцінок).
VІ Домашнє завдання та інструктаж до нього (2 хв.)
|
Домашнє завдання |
|
1. повторити § 5 стор. 42-45, 2. розв’язати вправи №№ 205, 212(а,б), 217* стор. 47 3*. Знайти область визначення ы множину значень функції:
а) |


про публікацію авторської розробки
Додати розробку