Урок з теми "Суміжні кути"

____ ________________ 20___ р.

 ^{[ дата ]}

Тема: Суміжні кути

Мета:

• Навчальна: засвоїти поняття суміжних кутів; довести та засвоїти основну властивість суміжних кутів; навчати знаходити градусну міру кута, що є суміжним з даним;

• Розвиваюча: розвивати вміння аналізувати отримані знання, правильно користуватися креслярським приладдям; будувати та вимірювати кути;
• Виховна: виховувати інтерес до вивчення точних наук;

Компетенції:

• математичні
• комунікативні

Тип уроку: засвоєння нових знань;

Обладнання: конспект, презентація, мультимедійне обладнання;

 

Хід уроку

1. Організаційний етап

• Привітання
• Перевірка присутніх на уроці
• Налаштування на роботу

 

2. Актуалізація опорних знань

• Які промені називаються доповняльними?
• Який кут називається розгорнутим?
• Якою є градусна міра розгорнутого кута?
• Сформулюйте основну властивість вимірювання кутів
• Що таке аксіома?
  

3. Вивчення нового матеріалу

 

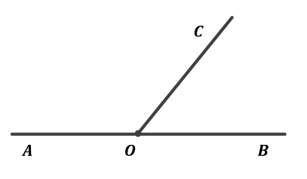>> Суміжні кути <<

 

 

     Що можемо сказати про кути і ?

(Ці кути мають спільну сторону (промінь ) а дві інші сторони (промені і є доповняльними))

 

 

 

 

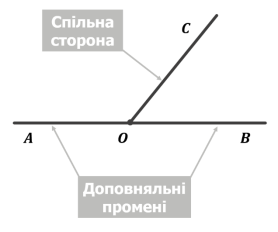
Означення

Два кути називаються суміжними, якщо вони мають спільну сторону, а інші сторони цих кутів є доповняльними променями.

 

 

 

 

Суміжними можуть бути не тільки кути. Суміжний – той, що межує з ким-, чим-небудь, прилеглий до чогось. Не будь-які два кути зі спільною межею називають суміжними, наприклад:

 

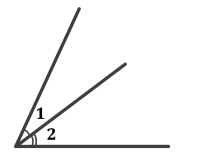
     Чи є суміжними кути 1 і 2? Чому?

(Ні. Ці кути задовольняють першу умову, тобто мають спільну сторону, але інші сторони цих кутів не є доповняльними променями)

 

 

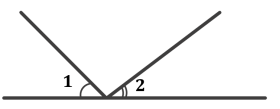
     Чи є суміжними кути 1 і 2? Чому?

(Ні. Ці кути задовольняють другу умову, тобто сторони цих кутів є доповняльними променями, але вони не мають спільної сторони)

 

 

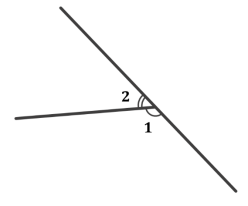
     Чи є суміжними кути 1 і 2? Чому?

(Так. Ці кути є суміжними так як вони мають спільну сторону а іншу сторони цих кутів є доповняльними променями)

 

 

 

 

 

>> Властивість суміжних кутів <<

 

Теорема – це математичне твердження, справедливість якого встановлена за допомогою міркувань.

Доведення теореми – міркування, що підтверджують справедливість математичного твердження.

Щоб довести теорему можна посилатися на раніше вивчені аксіоми чи означення.

 

Увага! Доведення теореми тісно супроводжується анімацією в презентації так, щоб діти бачили, як треба правильно оформлювати доведення в конспекті

 

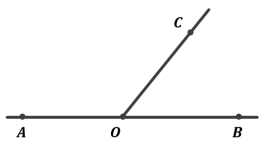
Теорема (властивість суміжних кутів)

Сума суміжних кутів дорівнює

 

 

 

 

 

     Поміркуйте, як можна довести дану теорему?

(Учні висловлюють власну думку)

 

     Що нам дано в умові теореми?

(Учні висловлюють власну думку)

 

     Що нам необхідно довести?

(Учні висловлюють власну думку)

 

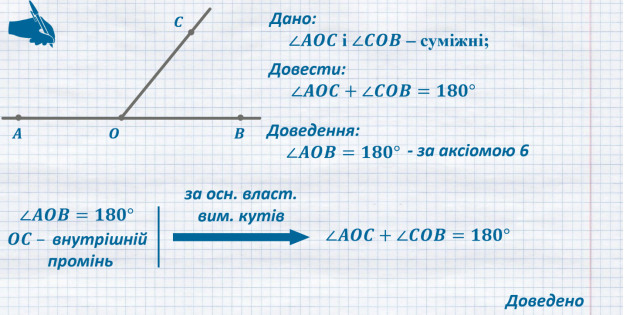
Дано:

і – суміжні;

 

Довести:

 

Доведення:

 

     Поясніть, чому

(Учні висловлюють власну думку)

 

З означення суміжних кутів слідує, що промені і є доповняльними, отже вони утворюють розгорнутий кут. Ми вже знаємо, що за аксіомою 6 - градусна міра розгорнутого кута дорівнює , отже:

 

- за аксіомою 6

 

     Пригадайте основну властивість вимірювання кутів, який можемо зробити висновок?

(Учні висловлюють власну думку)

 

Так як , – внутрішній промінь  кута і за основною властивістю вимірювання кутів градусна міра кута дорівнює сумі градусних мір кутів, на які він розбивається будь-яким променем, що проходить між його сторонами, то

 

 

 

Доведено.

*Запис у зошиті:

>> Наслідки з теореми про властивість суміжних кутів <<

 

     Твердження, що безпосередньо випливають із теорем (чи аксіом), називають наслідками

 

Наслідок 1

Кут, суміжний з прямим кутом, - прямий

 

Наслідок 2

Кут, суміжний з гострим кутом, - тупий, кут суміжний з тупим кутом, - гострий.

 

     Обґрунтуйте ці наслідки

(Учні висловлюють власну думку)

 

Отже, щоб довести теорему або розв’язати геометричну задачу, необхідно посилатися на раніше вивчені означення, аксіоми, теореми чи їх наслідки а також дані, що містяться в умові задачі або випливають із неї.

 

4. Закріплення нових знань та вмінь учнів

№1

Чи можуть два суміжні кути дорівнювати:

1.     і
2.     і
3.     і
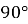4.     і

 

Розв’язок:

Так як сума суміжних кутів дорівнює , то:     - не суміжні     - суміжні     - суміжні     - не суміжні

 

№2

Знайдіть кут, суміжний з кутом:

1.     ;
2.     ;

 

Розв’язок:

Так як сума суміжних кутів дорівнює , то:

1.    

 

2.    

 

Відповідь: 1) ; 2)

 

№3

Накресліть за допомогою транспортира . Побудуйте суміжний з ним кут за умови, що  – їх спільна сторона. Обчисліть його градусну міру.

 

Розв’язок:

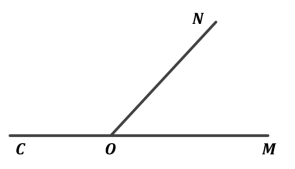
*Рисунки учнів можуть відрізнятися

 

– суміжний з кутом

 

Так як сума суміжних кутів дорівнює , то:

 

 

 

Відповідь:

 

№4

Промінь, що проходить між сторонами кута, ділить його на кути, що дорівнюють і . Знайдіть градусну міру кута, суміжного з даним.

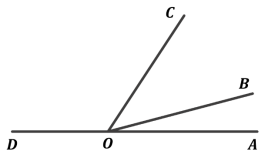
Дано:

;

;

– суміжний з кутом ;

 

Знайти:

- ?

 

Розв’язок:

За основною властивістю вимірювання кутів:

 

Так як сума суміжних кутів дорівнює , то:

 

Відповідь:

 

№5

Якщо суміжні кути рівні, то вони прямі. Доведіть це твердження

 

Доведення:

Сума суміжних кутів дорівнює , так як кути рівні умовою то нехай їх градусна міра дорівнює , отже:

 

Доведено.

 

№6

Знайдіть суміжні кути, якщо один з них на менший від іншого.

 

Дано:

– суміжні;

на ;

 

Знайти:

- ?

- ?

 

Розв’язок:

Нехай , тоді

Так як сума суміжних кутів дорівнює , то:

 

Отже:

 

Відповідь: і

№7

Знайдіть кут між бісектрисами суміжних кутів.

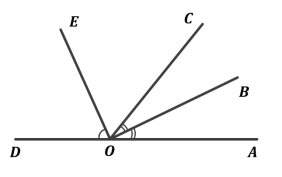
Дано:

і – суміжні;

і – бісектриси;

 

Знайти:

–  ?

 

 

 

Розв’язок:

Так як і – суміжні, то:

;

 

Так як і – бісектриси, то:

 

За основною властивістю вимірювання кутів:

 

Відповідь:

 

5. Підсумок уроку

• Які кути називаються суміжними?
• Чому градусна міра суміжних кутів дорівнює ?
• Як за градусною мірою кута знайти градусну міру суміжного з ним кута?
• Якими є два кути, якщо суміжні з ними кути рівні?

(Вони рівні – це твердження учням треба буде довести в д/з №93)

• Який кут утворюють бісектриси суміжних кутів
• Якщо два суміжних кути є рівними, якою є їх градусна міра?

 

6. Домашнє завдання

Опрацювати §4-5
Виконати № 83, 85, 87, 93, 95