Урок "Заміна змінних при розв'язуванні тригонометричних рівнянь"

Тема: Заміна змінних при розв’язуванні тригонометричних рівнянь

Розв’язування тригонометричних рівнянь зведенням до однієї функції.

 

Мета:

Навчальна: формування в учнів умінь розв’язувати тригонометричні

                     рівняння способом зведення до однієї функції (алгебраїчним 

                     способом);

Розвиваюча: розвивати логічне мислення , мимовільну та довготривалу

                        пам'ять, формувати культуру математичних записів;

Виховна:       виховувати уважність, дисциплінованість.

Обладнання:мультимедійна дошка.

Тип уроку: вивчення нового матеріалу.

Хід уроку

І. Організаційна частини.

Оголошення теми та мети уроку.

ІІ. Перевірка домашнього завдання.

Перевірити наявність домашнього завдання, в разі потреби розв’язати  

    завдання біля дошки.

(завдання 

спроектовано на екран)

 

 

1.    
2.     ;
3.    
4.    

 

1.    
2.    
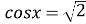
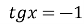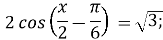
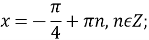
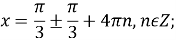
3.     Рівняння розв’язків не має
4.    

 

 

1.    

2.     ;

3.    

4.    

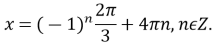
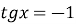ІІІ. Актуалізація опорних знань.

Яке рівняння називається тригонометричним?

(Тригонометричним рівнянням називається рівняння, в якому невідоме   

 входить під знак тригонометричної функції).

Які найпростіші тригонометричні рівняння ви знаєте і які їх розв’язки ?

().

 

IV. Вивчення нового матеріалу.

На попередніх уроках ми вивчали найпростіші тригонометричні рівняння  і навчилися їх розв’язувати. На сьогоднішньому уроці ми розглянемо тригонометричні рівняння, розв’язання яких зводиться до розв’язання найпростіших рівнянь за допомогою перетворень тригонометричних виразів та заміни змінних.

Метод заміни змінної нерідко зводиться до найпростіших тригонометричних рівнянь, або до алгебраїчних.

Даний метод розв’язання розглянемо на прикладі.

Розв’яжіть рівняння. (рівняння спроектовано на екран)

Це рівняння є квадратним відносно . Введемо заміну, дістанемо рівняння.

Після розв’язання алгебраїчного рівняння необхідно виконати обернену заміну і розв’язати найпростіше тригонометричне рівняння.

Відповідь:

Розв’язування тригонометричних рівнянь зведенням до однієї тригонометричної функції також розглянемо на прикладі.

(рівняння спроектовано на екран)

Це рівняння є квадратним відносно . Введемо заміну, дістанемо рівняння:

Відповідь:

V. Закріплення вивченого матеріалу.

Розв’яжіть рівняння:

1)

Це рівняння є квадратним відносно . Введемо заміну,, дістанемо рівняння.

Відповідь:

2)

Це рівняння є квадратним відносно . Введемо заміну, дістанемо рівняння:

Відповідь:,

Клас ділимо на 4 групи. Кожна група отримує завдання. Один представник від кожної групи виконує завдання біля дошки.

Завдання:

1 група

А)

Б)

2 група

А)

Б)

3 група

А)

Б)

4 група

А)

Б)

Після розв’язання проводиться колективна перевірка виконаного завдання (представник 1 групи перевіряє завдання 4 групи і навпаки, а 2- 3).

 

VI. Повідомлення  домашнього завдання.

Вивчити параграф13(1) Виконати завдання 7,9 сторінка 121.

VII. Підсумок уроку.

Які способи розв’язання тригонометричних рівнянь ми сьогодні 

 розглянули?

Який алгоритм розв’язання тригонометричного методом заміни змінних?

За допомогою якої формули ми зводимо тригонометричне рівняння до однієї тригонометричної функції?

VIII. Оцінювання учнів.