Урок "Застосування інтеграла до обчислення площ плоских фігур"
| Дослідницький проекти / стрічка часу / Tiki-toki |
Творчій проект / відеоролік / VIDEOSCRIBE SPARKOL |
| Творчій проект / кросворд / MS Exsel Ігровий проект / вправа «Знайти пару» / Learning Apps Ігровий проект / вправа «Пазл» / Learning Apps |
| Інформаційний проект 1/ інтерактивна гра / MS Power Point Інформаційний проект 2/ інтерактивна гра / MS Power Point Практично-орієнтований проект / задачі з практичним змістом / Padlet |
Тестування / MyTestXProта Netop School |
| Оцінювання досягнень на уроці у Google таблицях відповіді на контрольні питання Вправа: закінчити речення, використовуючи 3 дієслова…/ Padlet |
| https://svetalena6811.wixsite.com/integralandplosha/domashnye-zavdannya |
![]()
![]()
![]() Дата проведення група
Дата проведення група
![]() Урок №
Урок №
Тема: Застосування інтеграла до обчислення площ плоских фігур.
Мета:
Навчальна: ввести поняття криволінійної трапеції. Формувати в учнів вміння застосовувати інтеграл для знаходження площ плоских фігур.
Розвиваюча: розвивати навики самостійного мислення, інтелектуальні навики (аналіз, сінтез, порівняння, співставлення), увагу, пам’ять. Формувати уявлення про ідеї , методи математики та її роль у пізнанні навколишнього світу та опануванні майбутньої професії, потреби у самоосвіті.
Виховна: формувати науковий світогляд та загальнолюдські духовні цінності. Виховувати інтерес до вивчення математики.
Тип уроку: комбінований (урок засвоєння нових знань та формування, вдосконалення знань, вмінь, навичок.
Вид уроку: захист проектів.
Методи та прийоми.
|
Методичні прийоми |
Етапи уроку |
|
Сценка у супроводі інфографіки |
Орг. момент |
|
Дослідницький проекти / стрічка часу / Tiki-toki |
Перевірка домашнього завдання |
Творчій проект / відеоролік / VIDEOSCRIBE SPARKOL |
Мотивація навчальної діяльності |
|
Творчій проект / кросворд / MS Exsel Ігровий проект / вправа «Знайти пару» / Learning Apps Ігровий проект / вправа «Пазл» / Learning Apps |
Актуалізація опорних знань |
|
Інформаційний проект 1/ інтерактивна гра / MS Power Point Інформаційний проект 2/ інтерактивна гра / MS Power Point Практично-орієнтований проект / задачі з практичним змістом / Padlet |
Вивчення нового матеріалу |
Тестування / MyTestXPro та Netop School |
Контроль і самоперевірка знань |
|
Оцінювання досягнень на уроці у Google таблицях відповіді на контрольні питання Вправа: закінчити речення, використовуючи 3 дієслова…/ Padlet |
Підсумок уроку Рефлексія |
|
https://svetalena6811.wixsite.com/integralandplosha/domashnye-zavdannya |
Домашнє завдання |
Підручники та обладнання:
- Математика:11 кл: підруч. для загальноосвіт. навч. закл.: рівень стандарту / Г.П. Бевз, В.Г. Бевз.- К: Генеза, 2011.-320 с.
- Опорні конспекти з теми
Програмне забезпечення:
- Сайт WIX
- Відкриті доступи до 9 Google акаунтів, Google таблиці
- MS Power Point, MS Word, MS Excel
- Net op School
- Videoscribe Sparcol
- MyTestXPro
- Advanced Grapher
- Larning Apps
- Padlet
Технічні засоби навчання. Комп’ютер (процесор: INTEL(R) Core (TM)I3 CPU: ОЗП (2 б), мультимедійний проектор, 9 персональних комп’ютерів підключених до локальної мережі та до мережі Інтернет
План:
- Оргмомент.
- Перевірка домашнього завдання
- Актуалізація опорних знань
- Мотивація навчальної діяльності
- Вивчення нового матеріалу
- Контроль і самоперевірка знань
- Підбиття підсумків уроку. Рефлексія.
- Інформація – інструктаж домашнього завдання.
ХІД РОБОТИ
Вища математика світу!
З СУМИ БЕЗКОНЕЧНО МАЛИХ
ВИНИКАЄ БЕЗКОНЕЧНО ВЕЛИКЕ.
Ліна Костенко
- Організаційний етап (перша сторінка сайту)
https://svetalena6811.wixsite.com/integralandplosha
Вітаю, гостей нашого уроку та учнів, які обрали класну чоловічу професію "Рихтувальник кузовів. Газоелектрозварник"
Вони вдало опановують як холодний жорстокий метал, так і полум'яну зварку.
Саме тому юнаків не збентежать незвичні умови уроку. І майбутні майстри рихтувальної та зварної справи покажуть себе інтелектуальними сучасними молодими людьми, достатньо соціалізованими, з певними громадянськими установами.
Чути скрегіт гальм та звук удару.
Клієнт заходить до СТО "Інтеграл" .
Клієнт (Шемчук Андрій): Мій транспортним засіб потребує кваліфікованого ремонту.Але мене цікавить:
- Чи маєти ви сертифікати, що підтверджують знання, уміння і навички;
- Та, звісно, ціна ремонту.
Майстер (Серьогін Валерій): Щоб задовольнити вашим умовам пропоную Вам ознайомитися з результатами проектів "Джерела великого відкриття", «Вивчив сам – навчи іншого», «Площі – від давнини до сучасності», «Світ, що нас оточує - це світ інтегрального та диференціального числення…» , «Кращий спосіб пояснити - це самому зробити…» .
(друга сторінка сайту)
https://svetalena6811.wixsite.com/integralandplosha/home
Вчитель.
Запишемо тему цього цікавого уроку. Застосування інтеграла до обчислення площ плоских фігур
На першому уроці теми «Первісна та її властивості», це місяць тому, учні почали працювати над проектами з вище названих тем. Сьогодні ми побачимо, послухаємо, оцінимо та використуємо результати їх роботи.
- Перевірка домашнього завдання
https://svetalena6811.wixsite.com/integralandplosha/admissions
(третя сторінка сайту)
Проект І
Я - керівник проекту. (Худницький Влад – показує стрічку часу онлайн –3D – click to find out more – прослухав – закрив …….)
Наш проект - дослідницька робота «Джерела великого відкриття»
Завдання проекту - дослідити історію виникнення інтегрального числення від давнини до сучасності. Описати внесок видатних вчених у створенні цього відкриття. Підкреслити значну роль вітчизняних математиків у появі цього великого знання.
Презентація результатів роботи над нашим проектом - стрічка часу «Обчислення площі довільної плоскої фігури за допомогою інтеграла. Джерела великого відкриття » , яка створена за допомогою онлайн сервісу Tiki-toki
Я - науковий редактор (Барановський Юрій/Балутін Вадим):
- Ідеї інтегрального числення беруть свій початок у працях стародавніх математиків. Про це свідчить «Метод вичеркувань» Евдокса
- Його ідеї наслідував Архімед. За його методом для обчислення плоскої фігури навколо неї описується і в неї вписується ступінчата фігура.
- Йоган Кеплер розвинув ідеї Архімеда у 17 ст. Кеплер відкрив закони руху планет. Він очислював площі фігур, об’єми тіл, спираючись на ідею розкладання фігури і тіла на нескінчену кількість малих частин
- Ісаак Ньютон (1643-1727) створив диференціальне й інтегральне числення за допомогою якого обчислювали площі й об’єми. Опубліковані ці факти у «Методі флюкцій». Ця праця містила термін змінної величини – флюєнти (первісна або невизначений інтеграл). Швидкість зміни флюєнт – флюксія (похідна)
- Готфрід Вільгельм Лейбніц. Незалежно від Ньютона Лейбніц також створив диференціальне та інтегральне числення. Він перший увів символ інтеграла , що нагадував розтягнену букву s (з латинської) перша буква слова summa «сума».
- Якоб Бернуллі. Бернуллі перший увів термін «інтеграл», що походить від латинського слова integer «цілий»
Я - творчий редактор (Антоненко Владислав):
- Михайло Васильович Остроградський, український матеманик досліджував проблеми математичного аналізу. Приятель Т. Шевченка
-

Михайло Пилипович Кравчук, український математик успішно працівав в галузі математичного аналізу
Майстер
Як кажуть, знаючи люди, розв'язання практичних задач механіки і геометрії показало, що що дифференціальне і інтегральне обчислення це навколишня реальність, перекладена на математичну мову.
Клієнт
Я в захваті від побаченого та почутого!
Вчитель.
Учасники інших проектів оцініть будь ласка роботу ваших друзів. Розробники цього проекту оцінить будь ласка власні результати. Я також оціню продукт ціх авторів, нагадаю їх ….
- Актуалізація опорних знань https://svetalena6811.wixsite.com/integralandplosha/academics
(четверта сторінка сайту)
Клієнт. Бажано ознайомитися з рівнем знань вашіх майстрів
Майстер. Вони знають і вміють виконувати завдання з теми та ще і інших навчають
Проект ІІ
Я - керівник проекту, дизайнер, розробник, тестувальник завдання №1.
(Бєлов Олег):
Наш проект - «Вивчив сам – навчи іншого»
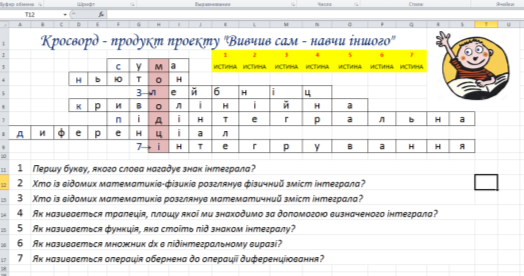
Завдання перше проекту – творча робота: скласти кросворд термінів з теми
Платформа – застосунок MS Exsel.
Формат презентації: відкриває документ, читає питання, вводить відповідь, зірочки роздає вчитель.

Вчитель. Вірна відповідь – зірочка. Команда проекту, яка матиме більшу кількість зірочок, отримає додатковий бал.
Я - дизайнер, розробник, тестувальник завдання №2.
(Радченко Сергій):
Наш проект - «Вивчив сам – навчи іншого»
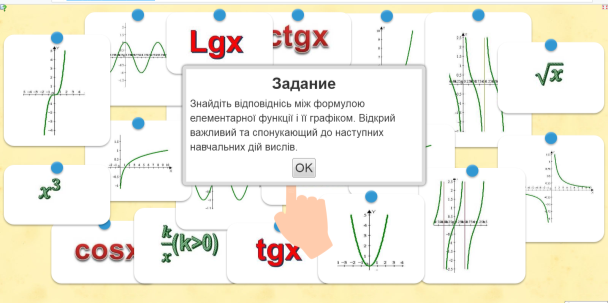
Завдання друге проекту - інтерактивна гра на знання опорних тем до вивчаємої теми
Платформа – онлайн застосунок LearningApps
Формат презентації: відкриває документ, наводить курсор на картинку з графіком функціє, учні називають відповідну йому формулу функції, тестувальник з’єднує пару, зірочки роздає вчитель.(Відповідь: графік ……є графіком функції, яка задана формулою …)
Я - дизайнер, розробник, тестувальник завдання №3.
(Оробченко Антон):
Наш проект - «Вивчив сам – навчи іншого»
Завдання третє проекту - інтерактивна гра на знання опорних тем до вивчаємої теми
Платформа – онлайн застосунок LearningApps
Формат презентації: відкриває документ, активує ![]() , учні називають пазл, що відповідає цій умові; активує
, учні називають пазл, що відповідає цій умові; активує ![]() , учні називають пазл, що відповідає цій умові; тестувальник відкриває пазли, зірочки роздає вчитель.(Відповідь: первісна функції … у точці …. дорівнює 1 або 4)
, учні називають пазл, що відповідає цій умові; тестувальник відкриває пазли, зірочки роздає вчитель.(Відповідь: первісна функції … у точці …. дорівнює 1 або 4)

Вчитель. Учасники інших проектів оцініть будь ласка роботу ваших друзів. Розробники цього проекту оцінить будь ласка власні результати. Я також оціню продукт ціх авторів, нагадаю їх ….
- Мотивація навчальної діяльності https://svetalena6811.wixsite.com/integralandplosha/news-and-events
(пята сторінка сайту)
Клієнт. Невже математичні знання допоможуть?
Майстер. Подивимося рекламний ролік
Проект ІІІ
Я - керівник проекту. (Данильчук Олег)
Наш проект – творча робота «Площі від давнини до сучасності»
Завдання проекту - дослідити історію обчислення площин людством від давнини до сучасності, від елементарних геометричних фігур до довільних плоских фігур.
Презентація результатів роботи над нашим проектом - рекламний ролік до теми "Застосування інтеграла до обчислення площ плоских фігур"створений за допомогою програми VIDEOSCRIBE SPARKOL, що допомагає створювати мальовані незвичайні комікси.
Творчий редактор (Ніконоров Гордій) – звук, зміст
Текст автора
Сцена1. У давнину, щоб вижити люди займалися землеробством
Сцена2. Тільки родючи ділянки давали добрі врожаї, а їх хозяїн отримував надлишки
Сцена3. Які обмінювалися на інструменти та засоби розкоші
Сцена4. Змінювався соціальних статус власників ціх ділянок
Сцени 5, 6, 7. Математики стародавнього Єгипту, Кітаю та Індії користувалися формулами площ плоских фігур, які є актуальними і у сучасному світі
Сцени 8, 9. Ця споруда складена з трикутників та квадратів, формули площі яких відомі людству багато століть
Сцена 10. Нас оточують предмети, які мають форму кола.Формулою площі якого користуються вчені не одну тисячу років
Сцена 11, 12 . Довгу історію мають формули плош ромба та трапеції
Сцена 13. Формула площі прямокутника зустрічається у наукових трактатах стародавніх цивілізацій
Сцена 14 . А якої форми це пошкодження? І якщо, я не знаю, що це за фігура, як я знайду формулу для обчислення її площі . Ось це і не тільки я буду знати, коли вивчу тему «Обчислення площ плоских фігур за допомогою інтеграла»
Я - технічний редактор (Масюткін Кирило) – відповідаю за монтаж та демонстрацію результату проекту:
Вчитель. Учасники інших проектів оцініть будь ласка роботу ваших друзів. Розробники цього проекту оцінить будь ласка власні результати. Я також оціню продукт ціх авторів, нагадаю їх ….
- Вивчення нового матеріалу https://svetalena6811.wixsite.com/integralandplosha/student-life
"Доводиться бігти з усіх ніг лише для того, лише для того щоб залишитися, на тому самому місці. Якщо хочеш потрапити в інше місце, потрібно бігти вдвічі швидше"
Льюіс Керол "Аліса в країні чудес"
Розробники V проекту працюють у дошки з отриманими завдяннями (закінчив сів на своє місце). Учасники IV проекту працюють в цей час з групою у комп’ютера, по черзі
Проект ІV
Я - керівник проекту, дизайнер, розробник, тестувальник завдання №1.
(Пермяков Віталій):
Наш проект - «Світ, що нас оточує - це світ інтегрального та диференціального числення . Тож давайте його пізнавати…»
Завдання перше проекту – інформаційна практично-орієнтована робота, на осмислення означення криволінійної трапеції
Означення
Фігуру обмежену
- графіком неперевної функції y=f(x)
- відрізком [a;b] осі Ox
- прямими x=a, x=b
Називають криволінійною трапецією.
Платформа –програма MS Power Point
Формат презентації: відкриває документ, читає питання (Які з фігур є криволінійними трапеціями?) , обирає варіанти креслень відповідно відповідям друзів відповідь, зірочки роздає вчитель.
Інструкція
- Якщо при натисканні на малюнок з фігурою з'явиться радісний смайлик, ваша відповідь правильна!
-
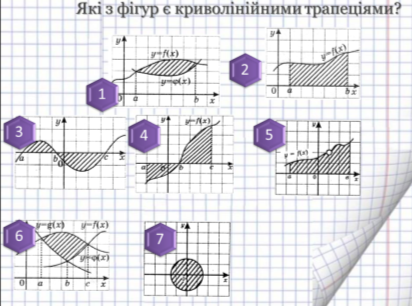
Якщо при натисканні на малюнок з фігурою ви почуєте неприємний звук, ваша відповідь неправильна!
Я - дизайнер, розробник, тестувальник завдання №2.
(Щербина Вадим)
Наш проект - «Світ, що нас оточує - це світ інтегрального та диференціального числення . Тож давайте його пізнавати…»
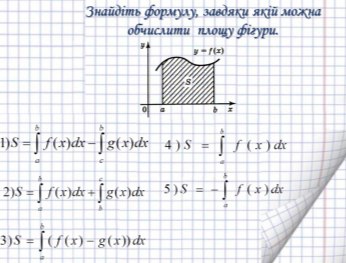
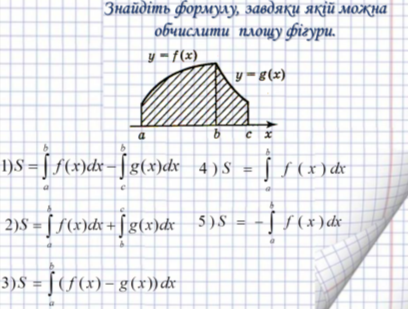
Завдання друге проекту – інформаційна практично-орієнтована робота, на свідоме розуміння геометричного зміста інтеграла
Геометричний зміст інтеграла - це площа криволінійної трапеції, яка обчислюється за формулою Ньютона - Лейбніца
Платформа –програма MS Power Point
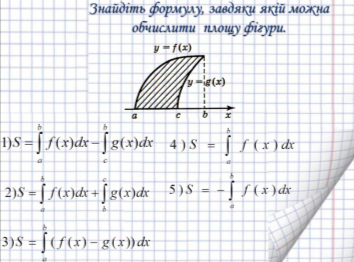
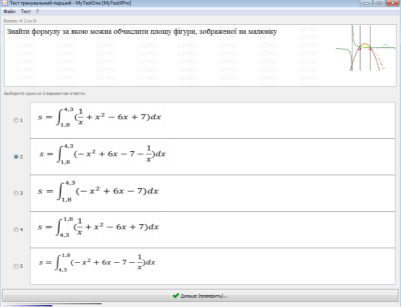
Формат презентації: відкриває документ, читає питання (Знайдіть формулу, завдяки якій можна обчислити площу фігури), обирає варіанти креслень відповідно відповідям друзів відповідь, зірочки роздає вчитель.
Інструкція
- Якщо при натисканні на малюнок з потрібною формулою з'явиться радісний смайлик і ви почуєте оплески, ваша відповідь правильна!
- Якщо при натисканні на малюнок з формулою ви почуєте барабанну дріб, ваша відповідь неправильна!
Вчитель. Учасники інших проектів оцініть будь ласка роботу ваших друзів. Розробники цього проекту оцінить будь ласка власні результати. Я також оціню продукт ціх авторів, нагадаю їх ….


Проект V (до дошки виходить розробник першого завдання і керівник проекту)
Я - керівник проекту, тестувальник завдань
(Вінокуров Дмитро):
Наш проект - "Кращий спосіб пояснити - це самому зробити"
Завдання проекту – інформаційна практично-орієнтована робота: розв’язок задач на застосування інтеграла у майбутній профсії
Зміст та результати проекту записані на онлайн дошці Padlet (показує і згортає вікно браузера з нею)
Практична перевірка аналітичного розв'язання виконується за допомогою програми Advanced Grapher (відкриває вікно цього застосунку)
Я - дизайнер, розробник завдання №1
(Філімонов Олександр)
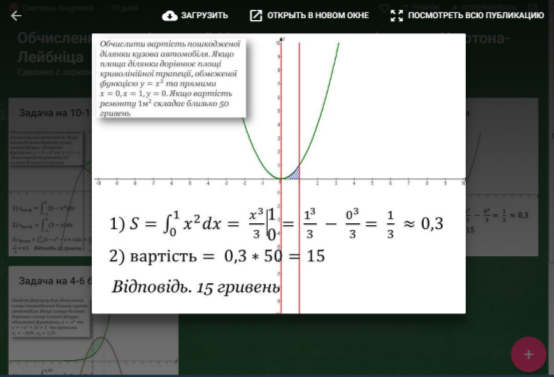
Формат презентації: записує розв’язання на дошці, коментує кроки виконання. (Учні у конспекти)
КОМЕНТАР
-
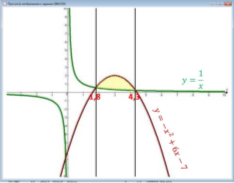
На малюнке криволінійна трапеція обмежена: параболою
 та прямими y=0 (вісь Х), х = 0 , х = 1, площа якої обчислюється за формулою Ньютона-Лейбніца
та прямими y=0 (вісь Х), х = 0 , х = 1, площа якої обчислюється за формулою Ньютона-Лейбніца
- Площа дорівнює визначеному інтегралу на відрізку [0,1]
-
Первісна функції
 дорівнює
дорівнює 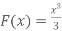
- Підставимо замість х 1, мінус потім – 0
- Площа дорівнює 0,3 кв.од
- Знаходимо вартість роботи
Керівник проекту, тестувальник завдань
(Вінокуров Дмитро):одночасно з товаришем по проекту
Формат презентації: виконує наступні дії , підводить підсумок (
Відповідь, що отримана при розв’язані задачі учнем і комп’ютером співпали.
Розв’язування задач за допомогою програми Advanced Grapher.
Виконаємо наступний алгоритм дій.
1. Запускаємо програму Advanced Grapher.
2. Будуємо в системі координат відповідні графіки функцій. Для цього заходимо в розділ «Побудова», вибираємо «Додати графік» та вписуємо формулу першої функції.
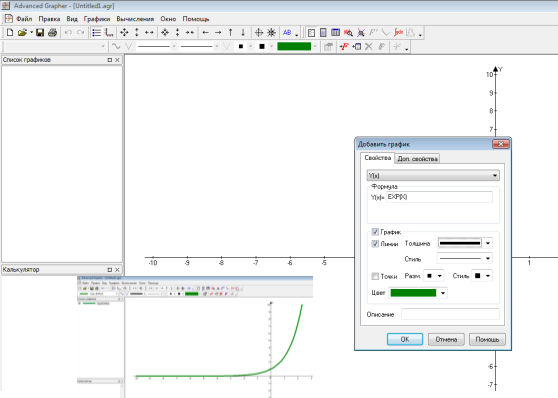
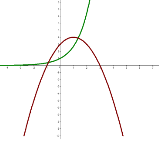
![]()

Керівник проекту, дизайнер, розробник, тестувальник завдання №1.
(Вінокуров Дмитро):
Аналогічно будуємо графік другої функції.
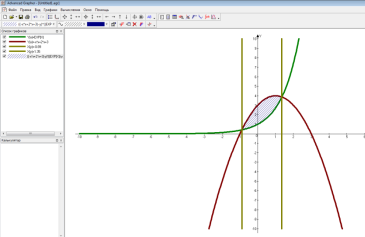
3. Визначаємо фігуру, площу якої треба знайти, та визначаємо межі інтегрування. Для цього заходимо в розділ «Обчислення», обираємо «Перетин», вводимо формули даних функцій та натискуємо клавішу «ОК». У вікні, яке з’явилося визначаємо межі інтегрування а = -0,89, b = 1,35 (див. рисунок). Будуємо їх, дивись п.2.
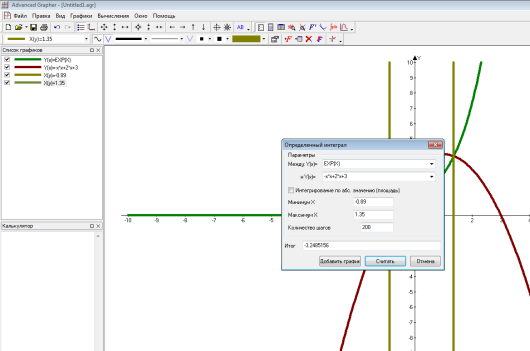
4. Заходимо в розділ «Обчислити», вибираємо «Інтегрування» та вказуємо основні лінії.
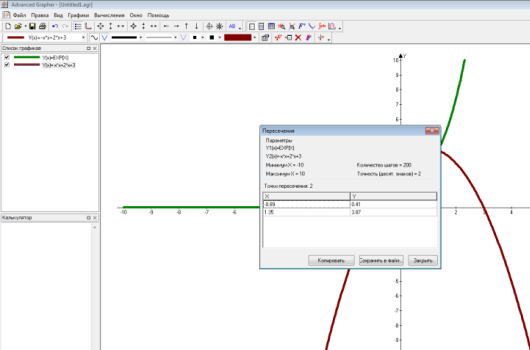
5. Дістаємо шукану площу S даної фігури (як видно з рисунка, S =3,2 ( кв.од). Для того щоб одержати візуально заштриховану область фігури, необхідно виконати такі дії: натиснути клавіші «Додати графік» та «ОК».
Я - дизайнер, розробник завдання №2
(Надєєв Євген)
Формат презентації: записує його розв’язання на дошці, коментує кроки виконання. (Учні у конспекти)(керівник проекту при виконанні цього завдання не працює!)
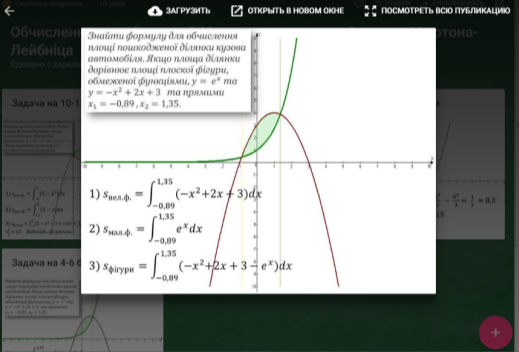
КОМЕНТАР
- На малюнке зображено плоску фігуру, що є перетином двох криволінійних трапецій, , площі яких обчислюються за формулою Ньютона-Лейбніца
- Велика криволінійна трапеція обмежена: параболою
![]() , прямими y=0 (вісь Х), х = -0,89 , х = 1,35 її формула…
, прямими y=0 (вісь Х), х = -0,89 , х = 1,35 її формула…
- Велика криволінійна трапеція обмежена: графіком функції
![]() , прямими y=0 (вісь Х), х = -0,89 , х = 1,35 її формула…
, прямими y=0 (вісь Х), х = -0,89 , х = 1,35 її формула…
- Площа плоскої фігури є різниця площ великої і маленької криволінійної трапеції
Я - дизайнер, розробник завдання №3
(Лапуха Микола)
Формат презентації: записує розв’язання на дошці, коментує кроки виконання. (Учні у конспекти) (керівник проекту при виконанні цього завдання працює паралельно на комп’ютері!)
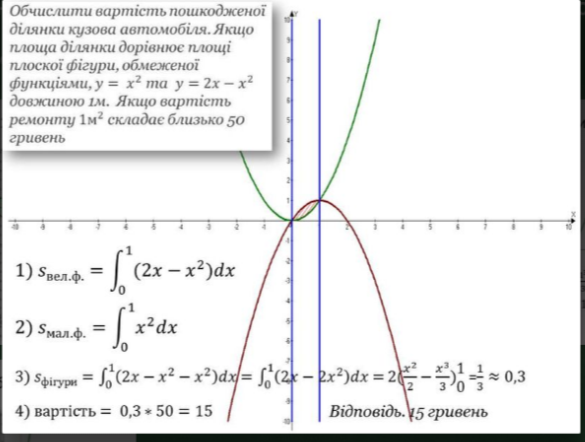
КОМЕНТАР
- На малюнке зображено плоску фігуру, що є перетином двох криволінійних трапецій, площі яких обчислюються за формулою Ньютона-Лейбніца
- Велика криволінійна трапеція обмежена: параболою
![]() , прямими y=0 (вісь Х), х = 0 , х = 1 її формула …
, прямими y=0 (вісь Х), х = 0 , х = 1 її формула …
- Маленька криволінійна трапеція обмежена: параболою
![]() , прямими y=0 (вісь Х), х = 0 , х = 1 її формула …
, прямими y=0 (вісь Х), х = 0 , х = 1 її формула …
- Площа плоскої фігури є різниця площ великої і маленької криволінійної трапеції
- Далі я обчислив визначений інтеграл та вартість ремонту
Керівник проекту, тестувальник завдань
(Вінокуров Дмитро):одночасно з товаришем по проекту
Формат презентації: виконує вже відомі дії , підводить підсумок
Відповідь, що отримана при розв’язані задачі учнем і комп’ютером співпали.
Я - дизайнер, розробник завдання №4
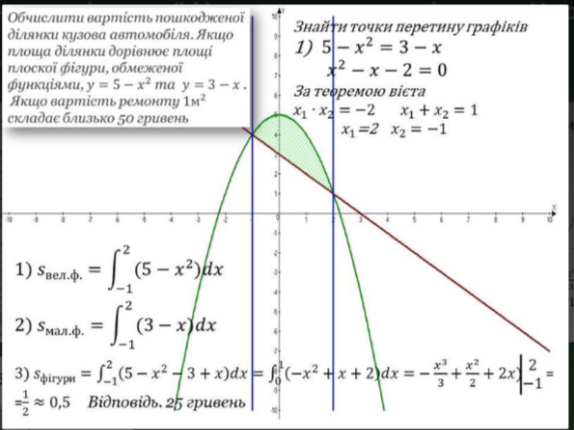
(Тимощенко Олександр, який закінчує своє завдання під час попередніх виступів)
КОМЕНТАР
- Спочатку я накреслив графік параболи у=5 - х2 , для цього параболу у= - х2 підняв вверх на 5 одиниць
- Потім я накреслив графік прямої у = 3 – х , для цього пряму у = - х підняв вверх на 3 одиниці
- Знайшов точки перетину прямої і параболи
- І отримав плоску фігуру, що є перетином двох криволінійних трапецій, площі яких обчислюються за формулою , площі яких обчислюються за формулою Ньютона-Лейбніца
- Велика криволінійна трапеція (зелена) обмежена: параболою
у=5 - х2 , прямими y=0 (вісь Х), х = - 1 , х = 2 її формула
- Маленька криволінійна трапеція (червона) обмежена: прямою
у = 3 – х прямими y=0 (вісь Х), х = - 1 , х = 2 її формула
- Площа плоскої фігури є різниця площ великої і маленької криволінійної трапеції
- Далі я обчислив визначений інтеграл та вартість ремонту
Керівник проекту, тестувальник завдань
(Вінокуров Дмитро):одночасно з товаришем по проекту
Формат презентації: виконує вже відомі дії , підводить підсумок
Відповідь, що отримана при розв’язані задачі учнем і комп’ютером співпали.
Вчитель. Учасники інших проектів оцініть будь ласка роботу ваших друзів. Розробники цього проекту оцінить будь ласка власні результати. Я також оціню продукт ціх авторів, нагадаю їх ….
- Контроль і самоперевірка знань https://svetalena6811.wixsite.com/integralandplosha/giving
(шоста сторінка сайту)
Запорука успішного виконання завдань ЗНО з теми будь - якого рівня складності
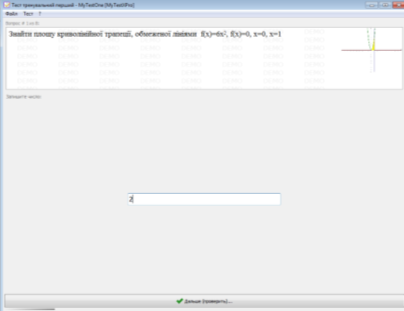
- цільонаправлене, поступове повторення. Сідайте за комп’ютери, щоб виконати тести, розроблені за матеріалами ЗНО з математики.
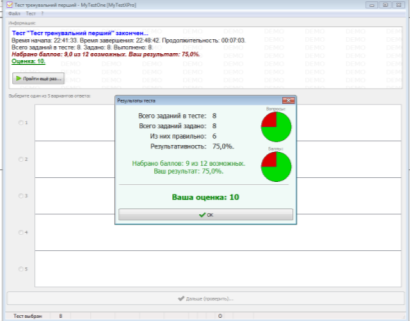
Учні виконують тести , за виконання яких отримують дві оцінки: перша – що виставить тестова програма, друга за записи у конспекті.
- Підбиття підсумків уроку. Рефлексія. https://svetalena6811.wixsite.com/integralandplosha/pppppppppp
(сьома сторінка сайту)
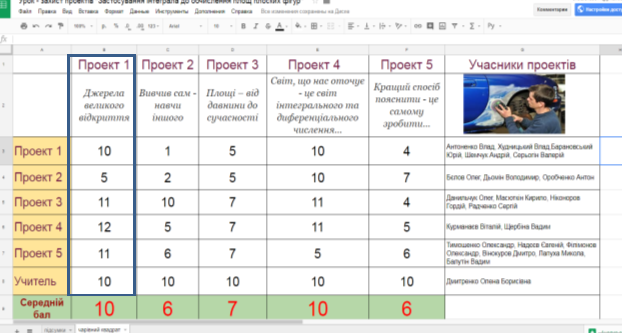
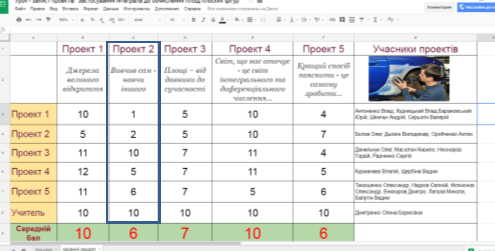
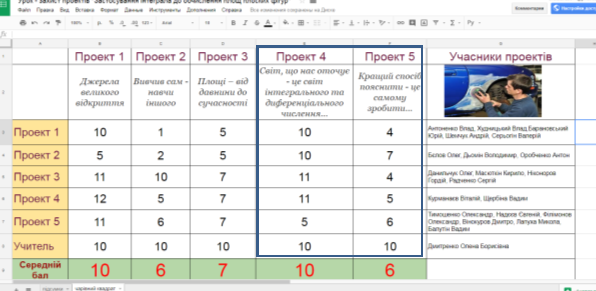
На протязі уроку учні оцінювали своі проекти та проекти друзів.
Оцінка за проект є середньою оцінок: які виставили безпосередньо учасники цього проекту; які виставили учасники їнших проектів; які виставив учитель (посилання на електронний журнал на моєму сайті (новини) сайт Елены Дмитренко або http://dmitrenkosv.ucoz.ua )
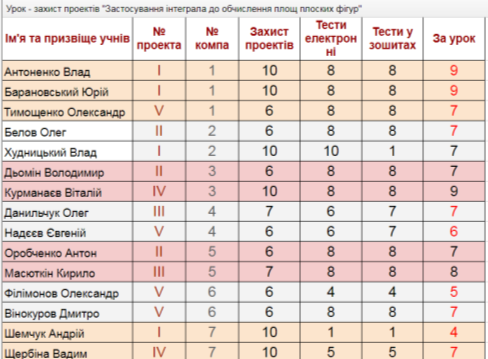
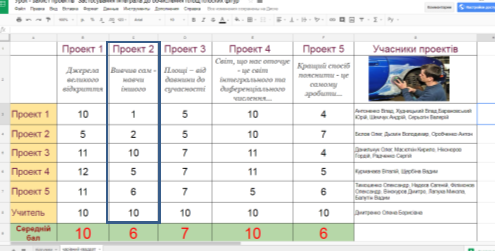
Сумісна робота організована за допомогою застосунку Google таблиці заповнення таблиці «Чарівний квадрат» колективна, частина таблиці «Підсумки» заовнюється автоматично (стовпчик «захист проектів»), інші стовпчики – викладачем.
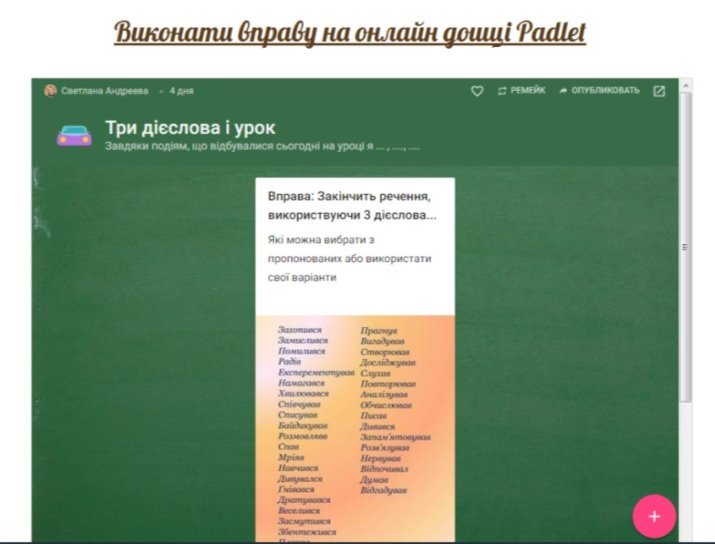
Після оцінювання учні відкривають онлайн дошку по посиланню на комп’ютерах або телефонах і виконують коротеньку вправу «Три дієслова і урок…» https://padlet.com/svetalena6811/2rc0ayh8hat6 , щоб описати свою діяльність на уроці.
Учасники опитування натискають значок + на онлайн дошці і у вікні, що з’явиться пишуть три дієслова з пропонованих або свої варіанти, які є продовженням речення. Завдяки подіям, що відбувалися на уроці я …. ,…. ,….. (підписи можна не ставити, ця вправа не оцінюється, якщо по техничним причинам ви не вспієте виконати цю роботу на уроці, зробить її вдома – посилання на моєму сайті (новини) сайт Елены Дмитренко або http://dmitrenkosv.ucoz.ua )
- Інформація – інструктаж домашнього завдання https://svetalena6811.wixsite.com/integralandplosha/domashnye-zavdannya
Домашня дослідницька робота
(восьма сторінка сайту)
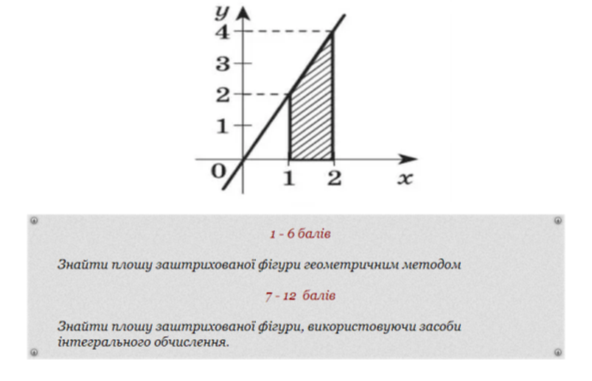
Закінчити урок хочу словами Ліни Костенко
Життя оперує безконечно малими.
Ми всі поодинці – також малі.
Але з усмішки, з потиску рук,
з брехні, убитої наповал,
історія – найскладніша з наук –
обчислює ЗОРЯНИЙ ІНТЕГРАЛ.
Із найдрібніших зоряних крихт!
Вища математика світу!
З СУМИ БЕЗКОНЕЧНО МАЛИХ
ВИНИКАЄ БЕЗКОНЕЧНО ВЕЛИКЕ.
Дякую за сумлінну працю на уроці!


про публікацію авторської розробки
Додати розробку