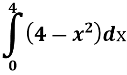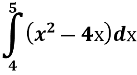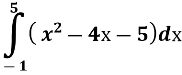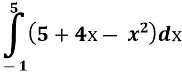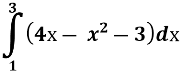Методична розробка уроку

«Застосування інтегралу. Розв’язування прикладних задач».

Державний навчальний заклад

«Регіональний центр професійної освіти будівельних технологій Харківської області»

Викладач математики Сидоренко Т.О.

Процес знаходження інтеграла називається інтегруванням. Цей процес зазвичай використовується при знаходженні таких величин як площа, об'єм, маса, зсув тощо, коли задана швидкість або розподіл змін цієї величини по відношенню до деякої іншої величини (розташування, час тощо).

Одного разу, прийшовши із рибалки, Архімед захотів визначити найбільш точно площу поверхні риби.

Зміст.

1.Вступ.

2. Мета, тип, форми і методи уроку.

3.План - схема уроку.

4. План конспект уроку.

5. Додатки.

5. Використовувані джерела.

Вступ.

Нова освіта складається в постійному пошуку методів і прийомів співзвучних часу, які так організовують життя того, хто навчається, що в подальшому він зможе спокійно, самостійно будувати своє життя. Чим би наші учні не займалися в майбутньому, хотілося б бачити їх вільними етичними та інтелектуальними особистостями. Відповідно до цього бажанням я впроваджую в роботі технологію критичного мислення. Учню повинно бути цікаво на уроці, інтерес - це синонім мотивації.

Тема програми: «Інтеграл та його застосування».

Важливим завершенням функціональної лінії курсу «Математика» є розгляд поняття інтеграла, яке є необхідним інструментом дослідження руху. Основні ідеї математичного аналізу виглядають досить простими і наочними, якщо викладати їх на тому інтуїтивному рівні, на якому вони виникли історично і який цілком задовольняє потреби загальноосвітньої підготовки учнів. Не варто захоплюватися формально-логічною строгістю доведень та відводити багато часу суто технічним питанням і конструкціям. Більше уваги слід приділити змісту ідей і понять, їх геометричному і фізичному тлумаченню.

Таке тлумачення буде основою для знайомства учнів з найпростішими диференціальними рівняннями, які широко використовуються для опису реальних процесів.

Ця тема є одною з найскладніших для сприйняття математики. Це обумовлено складністю самого матеріалу, слабо сформованої шкільної базою і обмеженою кількістю часу на її вивчення.

Тема уроку: «Використання інтегралу».

Урок побудований з використанням прийомів технології розвитку критичного мислення, спрямований на самостійне придбання і засвоєння нових знань. На уроці використовуються різні форми роботи: фронтальна, індивідуально-самостійна, групова, пошуково-дослідницька, в яких у учнів формуються вміння самостійно здобувати знання, робити висновки й умовиводи. Урок послужить розвитку пізнавальної діяльності учнів з даної теми. Дана форма проведення уроку стимулює пізнавальні інтереси у дітей. Зміна видів роботи дозволяє підтримувати увагу, працездатність і мотивацію на необхідному рівні.

На даному уроці учні підводять підсумки вивчення теми. Тут вони повторюють, узагальнюють основні теоретичні положення, закріплюють і систематизують основні методи і прийоми обчислення невизначеного і визначеного інтегралів, навчаються застосовувати знання при вирішенні конкретних практичних завдань.

Мета:

Вид діяльності на уроці: самостійна робота з самоконтролем, робота в групах, усні вправи, тести.

Міжпредметні зв’язки: геометрія, фізика, економіка, хімія, біологія.

Урок розрахований на 45 хвилин.

 

Словесні методи:

• розповідь;

• бесіда;

• використання ключових слів;

• коментар до виконання вправ;

• самооцінка;

• взаємонавчання;

• методи мотивації;

• збудження інтересу;

• стимулювання навчання.

Практичні методи:

• конкретно-індуктивний;

• розв'язування вправ;

• супровідного закріплення;

• самостійна робота;

• робота в групах;

• проскриптивний метод;

• метод повторення;

 • поступового ускладнення завдань.

Очікувані результати:

 учням необхідно

знати: 

- таблицю первісних елементарних функцій,

- правила знаходження первісних,

- формулу Ньютона - Лейбніца,

- таблицю інтегралів;

вміти : 

 - знаходити первісну з використанням таблиці  первісних та  правил        знаходження первісних,

- застосовувати формулу Ньютона – Лейбніца до обчислення  визначеного інтеграла,

- обчислювати за допомогою інтеграла площу криволінійної  трапеції,

- застосовувати інтеграл до розв’язування задач стереометрії, фізики, економіки, техніки, тощо.

План - схема уроку.

Структура і методи навчання.	Діяльність викладача.	Діяльність учнів
I. Орг. момент. (2 хв.) 1. Привітання. 2. Відсутні. 3 Релаксація.	Перевіряє явку і готовність учнів до уроку. Запис у журнал. Формує позитивний мікроклімат в класі.	Позитивний настрій на роботу. Концентрація уваги.
II. Перевірка Д.З. Актуалізація опорних знань. (10 хв.) 1.Д.З. учні перевіряють за правильним рішенням.   2. Виклик вже наявних знань по досліджуваному питанню: * Усне опитування. Метод «Інтерв’ю». (додаток №1) Вірна відповідь – 4 бала 3. Установіть відповідність між заданими фігурами та формулами для обчислення їхніх площ. (додаток №2) Вірна відповідь – 4 бала   4. Повторення застосування інтеграла. «Асоціативний кущ». (додаток 3)	Відповідає на запитання учнів   Контролює і коректує відповіді. Організовує узагальнення знань.	Виправляють помилки. Задають питання. Відповідають за бажанням. Узагальнюють засвоєний матеріал, закріплюють вивчене шляхом повторення. Озвучування виконаного завдання та запис у зошитах. Самостійна робота с самоперевіркой.
III. Мотивація навчальної діяльності. (2 хв.) 1.Бесіда. 2.Повідомлення теми і мети. 3. Проблемне питання. (додаток №4)	Повідомлення теми і мети уроку. Створення ситуації зацікавленості. Здійснює постановку завдань на урок.	Запис у зошит.
IV. Удосконалення вмінь і навичок. (15 хв.) 1. Розв’язування задач за допомогою викладача. Робота в групах.	Організовує закріплення навчального матеріалу. Організує узагальнення результатів. Консультує, підказує шляхи вирішення, вказує на помилки.	Осмислюють, поглиблюють розуміння матеріалу. Розв’язують задачі в групах. Запис вірного розв’язування на екране з поясненням представника групи, яка виконала це завдання.
V. Застосування знань і вмінь. (10 хв.) 1. Тестування. Розв’язування тестових завдань "Перевір себе". (додаток №5) Вірна відповідь – 1,5 бала	Організовує застосування знань і оцінює ступінь засвоєння.	Використовують знання, здійснюють самоперевірку.
VI. Підведення підсумків уроку. (4 хв.) Рефлексія. 1. Робота с асоціативним кущем. (додаток №6) 2. Метод «Чарівна скринька». 3.Оцінювання.	Прийом створення ситуації успішності. Пропонує поставити самім собі оцінку за роботу. Коментує і озвучує оцінки за урок. Визначає важливість зусиль учня в діяльності. Виставляє оцінки в журнал.	По черзі достають питання із шкатулки і відповідають на нього. Підраховують бали і оголошують свої оцінки.
VII. Домашнє завдання. (2 хв.) Диференційоване. Підготовка к контрольної роботі.	коментує	Обирають свій рівень. Запис у зошит.

План – конспект уроку.

«Недостатньо лише отримати знання, треба їх систематизувати і знайти їм гідне застосування».

Гете І.

I. Орг. момент.

Добрий день.

Для того, щоб добре працювати на уроці, потрібний відповідний настрій. Почнемо із вправи на увагу.

Дивимось і запам’ятовуємо.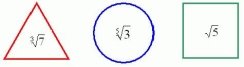


Декілька секунд учні дивляться на рисунок, а потім відповідають на запитання: 
1.    Перерахувати всі корені, які ви бачили. 
2.    У якій геометричній фігурі розміщений ? 
3.    Якого кольору це коло? 
4.    Квадратний корінь з якого числа знаходиться у квадраті? 
5.    Якого кольору цей квадрат? 

II. Перевірка Д.З. Актуалізація опорних знань.

1. Вашим домашнім завданням було розв’язати задачі з фізики, застосувавши поняття похідної.

Задача 1.

Робота, що виконується при стисканні пружини на х см задається рівнянням:  A(x) = 230x + 2x³. Яка сила пружності виникає в пружині при її стисканні на 2 см?

Розв’язування.

F(x) = A’(x);

F(x) = 230 + 6x²;

F(x) = 230 + 0,02² = 230,0024 (H).

Відповідь: 230,0024 (H).

Задача 2.

Нехай кількість речовини, що вступив в хімічну реакцію задається залежністю:

р (t) = + 3t -3 (моль)

Знайти швидкість хімічної реакції через 3 секунди.

Розв’язування.

υ(t) = P^’(t) = t + 3

υ(3) = 6

2. Усне опитування. Метод «Інтерв’ю».(додаток №1)

* Означення первісної.

(Первісною для функції f(x) називається така функція F(x), похідна якої F'(x) дорівнює f(x)).

* Основна властивість первісної.

(Якщо функція F(x) є первісною для функції  f(x) на даному проміжку, а  C  – довільна стала, то  F(x)+C  є також первісною для функції  f(x), при цьому будь-яка первісна для функції  f(x) на даному проміжку може бути записана у вигляді F(x)+C , де С – довільна стала).

* Правила знаходження первісної.

(Щоб знайти первісну суми скінченої кількості функцій, можна знайти суму первісних кожного доданка, якщо вони існують.

Щоб знайти первісну різниці двох функцій, можна знайти різницю первісних зменшуваного і від’ємника, якщо вони існують.

Щоб знайти первісну добутку функції і константи, можна знайти первісну функції і помножити її на цю ж константу.

Щоб знайти первісну складеної функції, внутрішня функція якої є лінійним виразом, можна первісну зовнішньої функції поділити на коефіцієнт при змінній внутрішньої функції.

Щоб знайти загальний вигляд первісних функції, треба знайти одну з первісних і додати до неї константу.)

* Які задачі приводять до поняття інтеграла?

(знаходження площ фігур межа яких складається з кривих ліній; задач з області механіки, фізики тощо).

* Формула Ньютона-Лейбніца.

= F(b) – F(a)

* Який геометричний зміст має визначений інтеграл?

(Геометричний зміст визначеного інтеграла — це площа криволінійної фігури (криволінійної трапеції), обмеженої віссю абсцис, двома вертикалями на краях відрізка і кривою графіка функції).

* Чи залежить значення інтеграла від вибору первісної для підінтегральної функції?

(ні).

* Встановити відповідність між формулою та фізичними величинами, які вона пов'язує. (додаток 1).

Вірні відповіді: 1-В. 2-А. 3-Б. 4-Д.

3. Установіть відповідність між заданими фігурами та формулами для обчислення їхніх площ. (додаток №2)

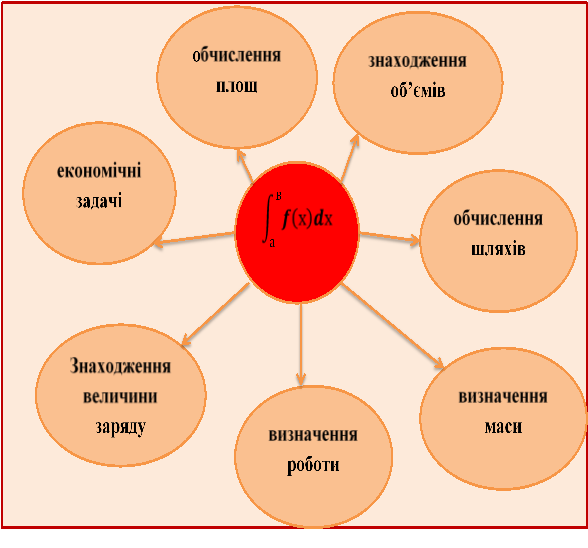
4. Повторення застосування інтеграла. «Асоціативний кущ». (додаток 3).

З якими областями застосування інтеграла мі вже познайомилися?

III. Мотивація навчальної діяльності.

1. Ми з вами сьогодні спробуємо за допомогою математики розв’язати  проблеми, що виникають на уроках геометрії, фізики економіки, тощо.

Альберт Ейнштейн говорив : "Наш досвід переконує нас, що природа – це реалізація найпростіших математичних ідей".

Будемо сподіватися, що ми переконуємося в істинності цих слів на сьогоднішньому уроці тема якого: «Інтеграл та його застосування».

До речі, задача (англ. problem) означає "проблема". Проблема розв’язування задач ускладняється в тому випадку, якщо вміння побачити єдину математичну модель у різних ситуаціях недостатньо розвинене. Але ж ще Анрі Пуанкаре, французький математик сказав: "Математика є спосіб називати різні речі одним ім’ям". Можливість розвивати ці уміння ви й матимете сьогодні, розв’язуючи задачі, пов’язані з геометрією, фізичними явищами, економічними процесами. І ви матимете чудову  нагоду закріпити і розвинути навички знаходити визначений інтеграл, застосовувати його при розв’язуванні практичних задач.

Інтеграл застосовують при знаходженні гальмування в в'язких середовищах, часу розрядки конденсатора, середніх значень різних величин, довжини кривих, часу скидання тиску через клапан; при дослідженні процесів горіння в різних опалювальних пристроях, чисельність популяції в біології. Скрізь, де деяка величина залежить від своїх похідних.

Це останній урок перед контрольною роботою.

2.Повідомлення теми і мети.

3. Проблемне питання. Задача 1.

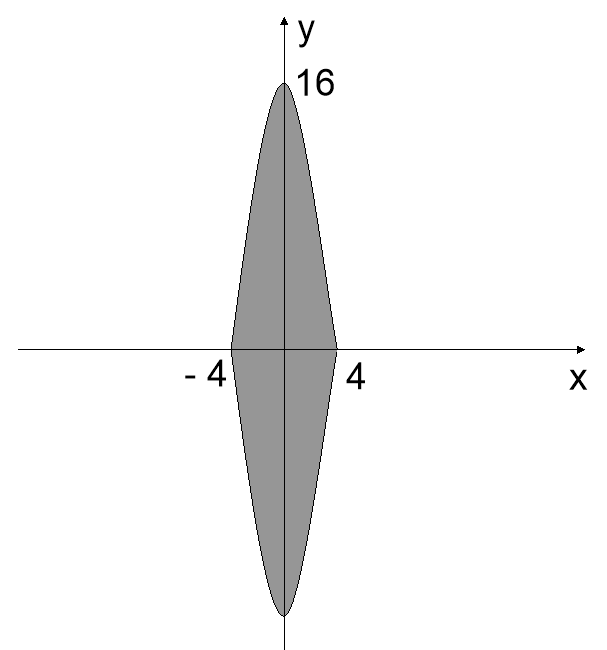
Я хочу відкрити магазин «Рай рибалки», в якому будуть продаватися товари для риболовлі та відпочинку. Торговий зал нагадує палубу корабля, найбільша відстань уздовж залу становить 16 метрів, найбільша відстань поперек залу - 12 метрів. Допоможіть розрахувати його площу. (додаток 4)

IV. Удосконалення вмінь і навичок.

1.               Розв’язування задач за допомогою викладача.

Задача 1. (проблемне питання).

Розв’язування.

Половина палуби є фігура обмежена графіком функції у = - х² + 16 і віссю ОХ

S = = 2(- + 16x = +64 - + 64) = 150 (м²)

Відповідь: S = 150 м².

Задача 2.

Швидкість зміни концентрації речовини, що вступила в реакцію, виражається функцією v = 3t + 1, де t – час (с), v – швидкість (моль/см³). Як зміниться концентрація речовини за час t₁=0 до t₂ =5 c?

Розв’язування:

Задача розв’язується методом безпосереднього інтегрування. Оскільки v(t)=C`(t) ,то C(t) – концентрація речовини і первісна для v(t), тому

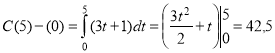(моль/м³).

Відповідь: 42,5 моль/м³.

Задача 3

Швидкість зростання популяції грибків пеніциліну при необмеженості ресурсів живлення описується експоненціальним законом

υ . Знайдіть приріст чисельності популяції ∆P за проміжок часу

∆t = t –t₀.

Розв’язування.

Задача також розв’язується методом безпосереднього інтегрування.

Приріст чисельності популяції

P = = = ( - ).

Задача 4.

Експериментально встановлено, що залежність витрати бензину автомобілем від швидкості на 100 км шляху визначається формулою
Q = 18 – 0,3v + 0,003v², де 30  v  110. Визначити середню витрату бензину при швидкості руху 50-60 км/год.

Розв’язання:

Середня витрата бензину становить

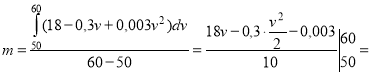
(л).

Відповідь: 10,6 л.

V. Застосування знань і вмінь.

Тести. (додаток 5)

Відповіді: 3, 5, 6, 10, 14, 20, 22.

VI. Підведення підсумків уроку.

Рефлексія.

1. Які області застосування інтеграла мі можемо додати до асоціативного куща?

(додаток 6).

2. «Чарівна скринька».

* Моя діяльність на уроці ( три дієслова )

Передати зміст своєї діяльності на уроці за допомогою трьох дієслів.

* Які види роботі виконували на уроці?

* Що мене здивувало?

* Які труднощі виникли? Чому, на ваш погляд? Як вони були подолані?

* Чи вдалося вам отримати відповіді на свої питання? На які питання ви хотіли б отримати відповідь?

* Які завдання з тих, що були на уроці, виявилися найпростішими, складними, цікавими ...? Чому?

* За що ти можеш себе похвалити?

* Над чим ще треба попрацювати?

2.Оцінювання.

VII. Домашнє завдання.

Середній.

1. Скласти список питань, на які, на ваш погляд, ми будемо відповідати на наступному уроці.
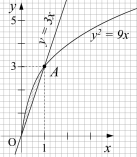
2.  Для функції f(x) = 4х³ знайдіть первісну, графік якої проходить через точку A (2;18).

Достатній.

1. Обчисліть інтеграл
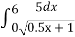
2. Знайдіть площу фігури, обмеженої графіками функцій y = x² + 2x + 2

і у = 2х = 3.

Для кмітливих.

1. З'ясувати в яких ще галузях використовується інтеграл. Доповнити до асоціативного куща.

2. Задача. Продуктивність праці робітника приблизно виражається формулою f(t) = − 0,0033t² – 0,089t + 20, 96, де t — робочий час (у годинах). Обчисліть обсяг продукції, випущеної протягом місяця, вважаючи, що робочий день триває 8 годин, а на місяць припадає 22 робочі дні.

Додаток № 1.

Усне опитування.

* Означення первісної.

* Основна властивість первісної.

* Правила знаходження первісної.

* Які задачі приводять до поняття інтеграла?

* Формула Ньютона-Лейбніца.

* Який геометричний зміст має інтеграл?

* Чи залежить значення інтеграла від вибору первісної для підінтегральної функції?

Встановити відповідність між формулою та фізичними величинами, які вона пов'язує.

1	S= t) t	А	Робота і  потужність
2	А = N(t) t	Б	Сила струму і електричний заряд
3	q = I(t) t	В	Швидкість руху і переміщення
4	Q = с(t) t	Г	Лінійна щільність і маса стрижня
		Д	Кількість теплоти і теплоємність

 

 

Додаток №2.

Установіть відповідність між заданими фігурами та формулами для обчислення їхніх площ.

1	Фігура, обмежена параболою у = х(х – 4) та прямою у = - 3.	А
2	Фігура, обмежена параболою у = х2 – 4х + 3 та прямою у = 3.	Б
3	Фігура, обмежена параболою у = х2 – 4х +3 та прямою у = 8.	В
4	Фігура, обмежена параболою у = х(х – 4) та прямими у = 0, х=5.	Г
		Д

 

Додаток №3.

Асоціативний кущ.

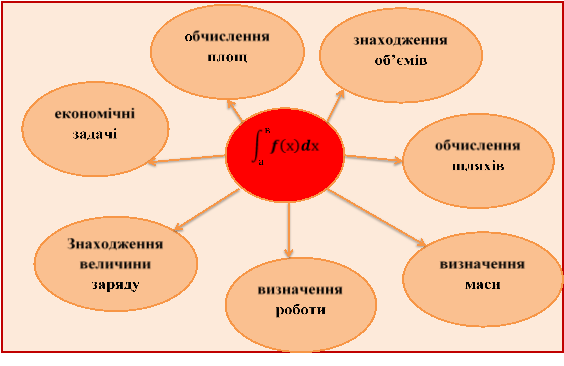
Додаток №4.

Проблемне питання.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

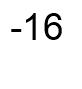
Додаток 5.

Тести.

1. За якою з наведених формул визначається площа даної фігури?

1. S =       2. S = – 3х)dx 3. S = 4. S =

2. Знайдіть в яких записах є помилка.

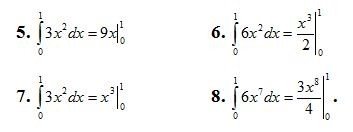
3. Швидкість руху змінюється за законом υ = 2t м / с. Знайти довжину шляху, пройденого тілом за 3-ю секунду його руху.

9.  S = (2t)’	10. S =
11. S =	12. S =

 

4. За якою з формул обчислюється обсяг виготовленої за перші 4 години продукції, якщо продуктивність праці задається формулою f(x)= 4x³?

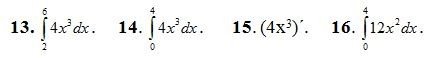
5. В якому випадку вірно обчислено навантаження електростанції за 3 години, якщо її витрати визначаються функцією f(х) = + 7t.

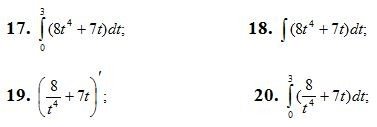
6. В якому з наведених випадків вірно визначений середній час, витрачений на засвоєння одного виробу від 10 до 20 виробів, якщо функція t= 3х описує зміни витрат часу t на виготовлення виробів в залежності від ступеня засвоєння виробництва.

 

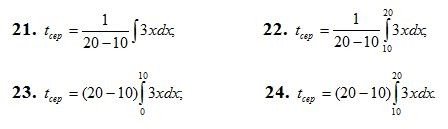
Додаток №6.

Асоціативний кущ.

 

Використовувані джерела.

1. Рачинська І.М. Технологія формування та розвитку критичного мислення. – Х.: Основа, 2013. -128 с.

2. Афанасьєва О.М.,Бродський Я.С., Павлов О.Л., Сліпенко А.К.Математика.11клас:Підручник для загальноосвітніх навчальних закладів. Рівень стандарту. - Тернопіль: Навчальна книга - Богдан, 2011.

3. Мерзляк А. Г., Полонський В. Б., Рабінович Ю. М., Якір М. С. Алгебра 11. – Збірник задач і контрольних робіт. – Харків, "Гімназія". – 2011. – 95 с.

4. Математика: 11 кл.: підруч. для загальноосвіт. навч. закл.: рівень стандарту / Г. П. Бевз, В. Г. Бевз. - К.: Генеза,2011.-320 с.: іл..-Бібліогр.:с.294.

5. http://osvita.ua/school/lessons_summary/math/43572/

6. http://metodportal.com/node/24456