Урок "Застосування похідної до розв'зяування прикладних задач"
Науково - методичне обґрунтування та актуальність теми
Характерною рисою сучасності є застосування математичних методів в різних областях людської діяльності.
Математика є не тільки знаряддям кількісного розрахунку, але також методом точного дослідження. Вона служить засобом гранично чіткого і ясного формулювання понять і проблем.
Диференціальне числення – одне з фундаментальних понять математики, іншими словами диференціальне числення – це опис навколишнього середовища, виконане на математичній мові. З його допомогою можна розв’язувати не тільки математичні задачі, а й задачі практичного характеру в різних областях науки та техніки.
Похідна функції використовується скрізь, де є нерівномірне протікання процесу: це і нерівномірний механічний рух, і змінний струм, і хімічні реакції, і радіоактивний розпад, і багато іншого. За допомогою похідної можна виконати розрахунки в короткі терміни.
Поняття похідної зустрічається ще в XV столітті. Великий італійський математики Нікколо Тарталья розглядав питання – наскільки залежить дальність польоту кулі від кута нахилу зброї.
Саме ж поняття похідної з’явилось дещо пізніше, в XXVII столітті та пов’язане з необхідністю розв’язання задач фізики та математики, в першу чергу: з визначенням швидкості прямолінійного руху та побудові дотичної до графіка функції.
Відкриттю похідної та основ диференціального числення передували роботи французьких математиків П’єра Ферма (1601 – 1665), який у 1629 р. запропонував способи знаходження найбільших і найменших значень функцій, проведення дотичних до довільних кривих, що фактично спиралися на застосування похідних, а також Рене Декарта (1596 – 1650), який розробив метод координат і основи аналітичної геометрії. У 1670-1671 рр. англійський математик і механік Ісаак Ньютон (1643 – 1727) і дещо пізніше у 1673 – 1675 рр. німецький філософ і математик Готфрід Вільгельм Лейбніц (1646 – 1716 ) незалежно один від одного побудували теорію диференціального числення .
І. Ньютон прийшов до поняття похідної, розв’язуючи задачі про миттєву швидкість, а Лейбніц – розглядаючи геометричну задачу про проведення дотичної до кривої.
Термін «похідна» ввів у 1797 р. французький математик Жозеф Луї Лагранж (1736 – 1813 ). Він ввів і сучасні позначення для похідної у вигляді ![]() та
та ![]() . До Лагранжа похідну за пропозицією Лейбніца називали диференціальним коефіцієнтом і позначали
. До Лагранжа похідну за пропозицією Лейбніца називали диференціальним коефіцієнтом і позначали![]()
![]() .
.
Цікавою є легенда про відшукання найбільшого значення функції, за якою засновниця м. Карфагену Дідона, дочка царя тірів, посварившись з братом Пігмаліоном, втекла від свого батька і після багатьох пригод з’явилася на південному узбережжі Середземного моря. Тут, у царя Нарбаса, за невеликі гроші вона купила шматок землі «не більше, ніж можна виміряти шкурою бика» – як зазначається в угоді. Місцеві жителі вважали умову буквальною і розраховували, що Дідоні для нового поселення дістанеться дуже маленький клаптик узбережжя. Проте спритна Дідона розрізала шкуру бика на найтонші смужки, зв’язала їх мотузкою і, закріпивши один її кінець на березі моря, пішла з іншим вздовж берега. Перед нею постало питання: яку форму потрібно надати мотузці, щоб «виміряти шкурою бика» найбільшу площу? Зокрема, це є задача на пошук замкненої кривої заданої довжини, що обмежує найбільшу площу. Виявляється, що такою кривою є коло. Дідоні, щоб розв’язати задачу, потрібно було обійти півколо з центром у точці О, довжина якого дорівнювала довжині мотузки.
Групу поділено на проектні групи, кожна з яких завчасно отримала домашнє завдання: знайти прикладну задачу, яку розв’язують за допомогою диференціального числення, розробити проект її розв’язання та презентацію до нього.
Основні вимоги
У результаті вивчення теми студенти повинні
Знати:
- Визначення похідної функції;
- Таблицю похідних;
- Правила диференціювання, похідну складеної функції;
- Геометричний та фізичний зміст похідної;
- Рівняння дотичної;
- Ознаки сталості функції; умови зростання та спадання функції, екстремуми функції;
- Правила знаходження найбільшого та найменшого значення функції на проміжку;
- Загальну схему дослідження функції;
Вміти:
- Знаходити похідні функцій;
- Застосовувати правила диференціювання до розв’язування задач;
- Складати рівняння дотичної до графіка функції в заданій точці;
- Знаходити проміжки зростання та спадання функції;
- Знаходити екстремуму функції та точки екстремуму;
- Проводити дослідження функції та побудувати графік;
- Знаходити найбільше та найменше значення функції на проміжку;
- Розв’язувати нескладні прикладні задачі на знаходження найбільшого та найменшого значень реальних величин;
Пряме не може бути кривим, а криве прямим. І все ж диференціальне числення, всупереч усім протестам людського розуму, прирівнює за певних умов пряме і криве одне до одного і досягає цим таких, яких ніколи не досягнути людському здоровому розумові.
Дане заняття буде підсумковим у вивченні теми «Похідна та її використання». Вашим домашнім завданням було повторити теоретичний матеріал з даної теми, а також підготувати цікаві задачі, в яких використовується похідна. .
Актуалізація опорних знань
- Сформулюйте означення похідної в точці;
- У чому полягає геометричний зміст похідної (фізичний зміст похідної)?
- Як знайти похідну добутку, частки, складеної функції?
- Що таке кутовий коефіцієнт прямої та чому він дорівнює?
- Що таке критичні точки? Як їх знайти?
- Що таке екстремуми функції та точки екстремуму?
Виконання вправ
Завдання 1. Укажіть в яких прикладах допущені помилки. Виправте їх.
|
|
Функція |
Похідна |
|
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
|
5 |
|
|
Завдання 2. Знайти проміжки зростання, спадання та точки екстремуму функції ![]() .
.
Розв’язання
-
 ,
, 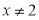 ;
;
-
Знайдемо похідну функції:
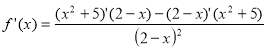 ;
;
![]() ;
;
![]()
![]()

![]() – критичні точки;
– критичні точки;

Функція зростає: ![]() ;
;
Функція спадає: ![]() ;
;
Точки екстремуму: ![]() ,
, ![]()
Завдання 3. Дослідити функцію та побудувати її графік ![]() .
.
Розв’язання
-
 ;
;
-
 – ні парна, ні непарна;
– ні парна, ні непарна;
Графік функції несиметричний ні відносно осі ординат, ні початку системи координат.
-
Точки перетину з віссю абсцис (нулі функції):
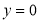 ,
, 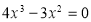 ;
;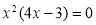
Отримаємо: ![]() або
або ![]() ;
;
Точки перетину з віссю ординат: ![]() ,
, ![]()
- Дослідимо функцію на зростання спадання та точки екстремму. Знайдемо похідну.
![]()
![]()
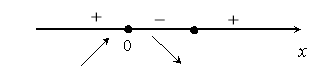
![]() – критичні точки.
– критичні точки.
![]()
Функція зростає: ![]() ;
;
Функція спадає: ![]() ;
;
Точки екстремуму: ![]() ,
, ![]() ;
;
Екстремуми функції: ![]() ,
, ![]() ;
;
- Будуємо графік (рис. 11)

Рис. 11
Завдання 4. На рисунку зображено графік функції ![]() і дотична до нього в точці з абсцисою
і дотична до нього в точці з абсцисою ![]() . Знайти значення похідної функції
. Знайти значення похідної функції ![]() в точці
в точці ![]()
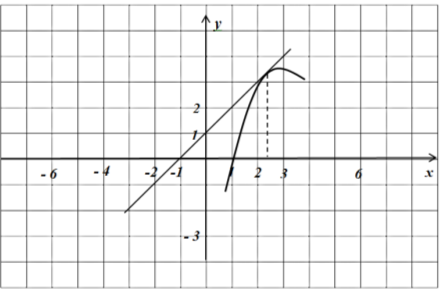
Рис. 1
Розв’язання
За геометричним змістом ![]() , тому задача зводиться до знаходження тангенса гострого кута (рис. 2).
, тому задача зводиться до знаходження тангенса гострого кута (рис. 2).
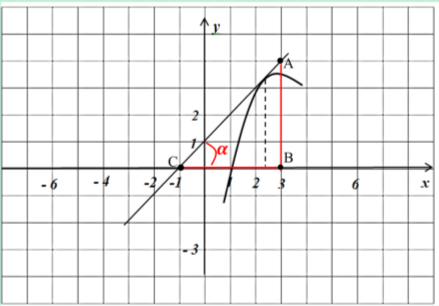
Рис. 2
![]()
Завдання 5. Скільки критичних точок має функція ![]() зображена на рисунку.
зображена на рисунку.
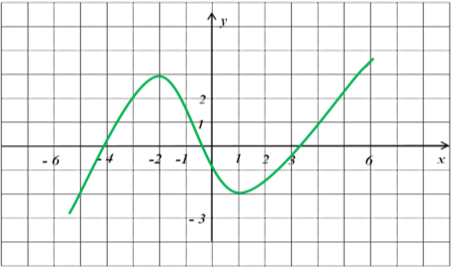
Рис. 3
Розв’язання
Так як на рисунку зображено графік функції ![]() , то критичними точками будуть ті точки, де функція змінює знак. Таких точок 2 (рис. 4)
, то критичними точками будуть ті точки, де функція змінює знак. Таких точок 2 (рис. 4)

Рис. 4
Завдання 6. Вказати проміжки спадання функції ![]() на відрізку [a;b], якщо на рисунку зображено графік похідної
на відрізку [a;b], якщо на рисунку зображено графік похідної ![]() .
.
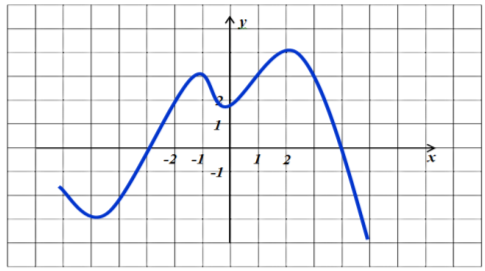
Рис. 5
Розв’язання
Так як на рисунку зображено графік похідної функції, то вихідна функція спадатиме на проміжку там, де похідна має від’ємний знак, тобто ![]()
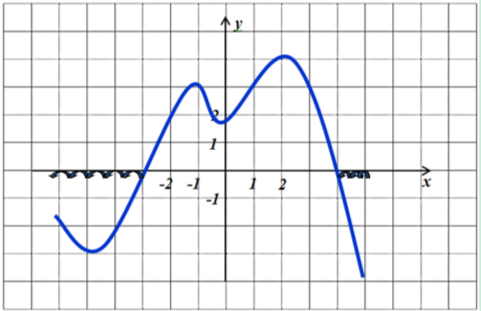
Рис. 6
Завдання 7. Вказати проміжки спадання функції ![]() на відрізку [a;b], якщо на рисунку зображено графік похідної
на відрізку [a;b], якщо на рисунку зображено графік похідної ![]() .
.

Рис. 7
Розв’язання
Так як на рисунку зображено графік похідної функції, то вихідна функція зростатиме на проміжку там, де похідна має додатній знак, тобто ![]() .
.
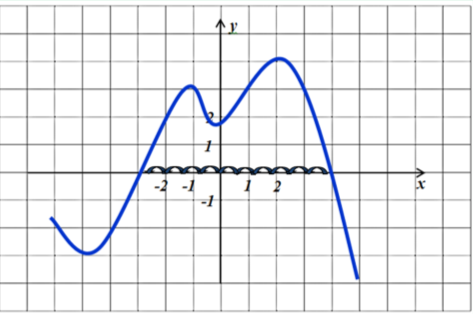
Рис. 8
Завдання 8. На рисунку зображено графік похідної функції ![]() на інтервалі (-7;7). Скільки точок екстремуму має функція?
на інтервалі (-7;7). Скільки точок екстремуму має функція?
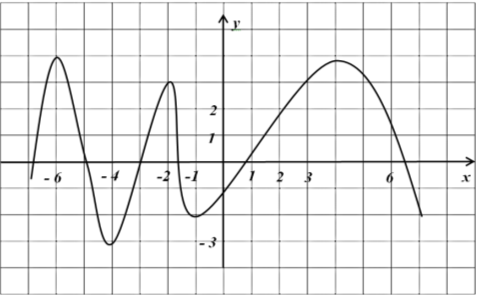
Рис. 9
Розв’язання
Так як на рисунку зображено графік похідної функції, то точки екстремуму будуть ті точки, де похідна змінює знак. На даному графіку таких точок 5 (рис. 10).
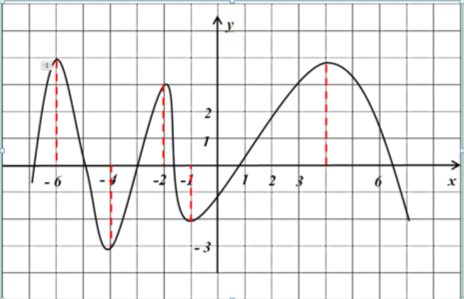
Рис. 10
Задачі прикладного характеру
- Задача геометричного змісту
Яким слід зробити нахил мосту, щоб перехід з мосту на схил був плавним, при довжині мосту 20 м і стріли підвісу 0,5 м.
Розв’язання
З точки зору математики міст має форму параболи, яку можна задати рівнянням ![]() . Так як довжина
. Так як довжина ![]() м, а стріла підвісу
м, а стріла підвісу ![]() м, то точки
м, то точки ![]() і
і ![]() є координатами кінцевих точок мосту.
є координатами кінцевих точок мосту.
З рівняння параболи ![]() . Маємо функцію
. Маємо функцію ![]() .
.
Для знаходження кута нахилу, використаємо геометричний зміст похідної ![]() . Для цього знайдемо похідну функції.
. Для цього знайдемо похідну функції.
![]() .
.
Знайдемо значення похідної в точці 10 ![]() .
.
Маємо: ![]() . Знаходимо обернену функцію
. Знаходимо обернену функцію ![]()

- Задача цариці Дідони
Парканом довжиною 80 м потрібно обгородити прямокутну ділянку найбільшої площі. Знайдіть розміри ділянки.
Розв’язання
Позначимо одну сторону прямокутника ![]() , тоді друга сторона буде дорівнювати
, тоді друга сторона буде дорівнювати ![]() , площа прямокутника
, площа прямокутника ![]() . З умови задачі випливає, що
. З умови задачі випливає, що ![]() . Таким чином, задача зводиться до знаходження найбільшого значення функції
. Таким чином, задача зводиться до знаходження найбільшого значення функції ![]() на відрізку
на відрізку ![]() .
.
Знайдемо похідну: ![]() . Знайдемо критичні точки:
. Знайдемо критичні точки: ![]() ,
, ![]() ,
, ![]() – належить проміжку
– належить проміжку ![]() . Знайдемо значення функції у критичній точці та на кінцях проміжку:
. Знайдемо значення функції у критичній точці та на кінцях проміжку:
![]()
![]()
![]()
Звідси отримуємо, що функція на інтервалі ![]() набуває найбільшого значення при
набуває найбільшого значення при ![]() .
.
Таким чином, із усіх прямокутників периметромом 80 м найбільшу площу має квадрат зі стороною 40 м.
- Задача фізичного змісту
Задача 1. При виверженні вулкану камені гірської породи викидаються перпендикулярно вгору з початковою швидкістю 120 м/с. Якої найбільшої висоти досягне каміння?
Увага!Речовина викидається перпендикулярно вгору. Висота каменя h дорівнює шляху ![]()
Розв’язання
Початкові умови: ![]() м/с.
м/с.
За фізичним змістом похідної: ![]() .
.
Знайдемо критичні точки функції: ![]() ,
, ![]() ,
, ![]() с.
с.
12,3 – критична точка максимуму, тоді![]() м
м
Задача 2. Автомобіль наближається до мосту зі швидкістю 72 км/год. Біля моста стоїть дорожній знак 36 км/год. За 7 с до виїзда на міст водій нажав на гальма. Чи з дозволеною швидкістю автомобіль виїхав на міст, якщо шлях зупинки визначається формулою ![]() ?
?
Розв’язання
Знайдемо швидкість автомобіля під час зупинки. Для цього знайдемо похідну даної функції: ![]() .
.
Гальмівний шлях за умовою задачі дорівнює 7 с. Обчислимо швидкість ![]() м/с.
м/с.
Переведемо отриману швидкість у потрібні одиниці виміру:
![]() м/с =
м/с = ![]() км/год =
км/год = ![]() м/год.
м/год.
Отже, автомобіль виїхав з дозволеною швидкістю.
- Задача біології
У живильне середовище вносять популяцію з 1000 бактерій. Чисельність популяції зростає за законом ![]() , t – виражається у годинах. Знайти через який час настане максимальний розмір цієї популяції.
, t – виражається у годинах. Знайти через який час настане максимальний розмір цієї популяції.
Розв’язання
![]() - закон зростання популяції. Для знаходження часу максимального розміру популяції, використаємо знаходження точок екстремуму. Для цього знайдемо похідну даного закону:
- закон зростання популяції. Для знаходження часу максимального розміру популяції, використаємо знаходження точок екстремуму. Для цього знайдемо похідну даного закону:
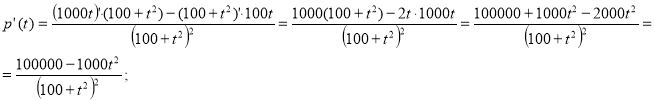 Знайдемо критичні точки, тобто прирівнюємо похідну до нуля.
Знайдемо критичні точки, тобто прирівнюємо похідну до нуля.

![]()
![]()
![]()
![]()
![]()
![]()
![]()
Маємо критичну точку ![]() год. Визначимо знак похідної на кожному проміжку.
год. Визначимо знак похідної на кожному проміжку.

Як бачимо, відбувається зміна знаку з «+» на «–», тому ця точка є точкою максимуму. Максимальний розмір популяції настане через 10 год.
- Задачі економіки
Задача 1. Розрахувати зміни продуктивності праці на початку робочого дня та за годину до її закінчення, якщо обсяг виготовлення продукції залежить від часу ![]() і описується рівнянням
і описується рівнянням ![]() ,
, ![]() – робочий день у годинах.
– робочий день у годинах.
Розв’язання
Згідно економічного змісту похідної продуктивність праці є похідною від обсягу виготовленої продукції.
![]() (од/год.)
(од/год.)
Знайдемо продуктивність праці на початку робочого дня та за годину до кінця.
![]() (од/год.);
(од/год.);
![]() (од/год.).
(од/год.).
Як бачимо, продуктивність праці на початку робочого дня вище, чим в кінці. Даний факт підтверджують і закони біології, і життєві спостереження.
Задача 2. На підприємстві виготовляють продукцію одного виду. Витрати на виробництво ![]() одиниць продукції виражається функцією
одиниць продукції виражається функцією ![]() , а дохід, отриманий від реалізації
, а дохід, отриманий від реалізації ![]() (у грн.). Визначте скільки продукції треба виготовити, щоб дохід був максимальний.
(у грн.). Визначте скільки продукції треба виготовити, щоб дохід був максимальний.
Розв’язання
![]() – витрати
– витрати
![]() – дохід, то прибуток
– дохід, то прибуток ![]()
![]() =
=![]()
Оскільки, за умовою задачі потрібно знайти кількість продукції, тому функцію розглядаємо на проміжку ![]() .
.
![]() ,
, ![]() ,
, ![]() – квадратне рівняння;
– квадратне рівняння;
![]()
![]() ,
, ![]() – критичні точки.
– критичні точки.
Проміжку ![]() належить одна критична точка,
належить одна критична точка, ![]() .
.
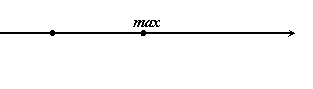
Дана точка є точкою максимуму, оскільки похідна змінює знак з «+» на «–». Обчислюємо прибуток ![]() - максимальний прибуток.
- максимальний прибуток.
- Використання похідної в задачах медицини
Концентрація ліків у хворого через деякий час після ін'єкції задається формулою ![]() . Знайти максимальну концентрацію і час, коли вона стане максимальною.
. Знайти максимальну концентрацію і час, коли вона стане максимальною.
Розв’язання
![]()
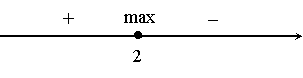
![]()
![]()
![]()
![]() або
або ![]()
![]() с.
с.
Максимальна концентрація досягне максимуму через 2 с і по величині буду дорівнювати ![]()
Задача 2. Розчинення лікарської речовини з таблетки описують рівнянням ![]() , де
, де ![]() – початкова маса на момент часу
– початкова маса на момент часу ![]() ;
; ![]() – нерозчинна маса на момент часу
– нерозчинна маса на момент часу ![]() ;
; ![]() – стала розчинення при заданих зовнішніх умовах. Визначте швидкість розчинення даної речовини за 30 хв, якщо
– стала розчинення при заданих зовнішніх умовах. Визначте швидкість розчинення даної речовини за 30 хв, якщо ![]() г,
г, ![]() .
.
Розв’язання
Масу лікарської речовини, що розчинилася на момент часу ![]() , записують у вигляді
, записують у вигляді ![]() Швидкість розчинення визначають за похідною:
Швидкість розчинення визначають за похідною: ![]() . Швидкість розчинення пропорційна масі розчиненої частини таблетки.
. Швидкість розчинення пропорційна масі розчиненої частини таблетки.
Нехай константа швидкості розчинення ліків дорівнює 0,02 ![]() , початкова маса 25 г. Розграхуємо швидксть розчинення препарату за 30 с.
, початкова маса 25 г. Розграхуємо швидксть розчинення препарату за 30 с.
![]() г маса розчиненої речовини;
г маса розчиненої речовини;
![]() г/с =
г/с = ![]() мг/с
мг/с
Задача 3. Ємність легенів людини, вік якої не менше 10 років наближено виражається формулою ![]() , де
, де ![]() – вік людини в роках,
– вік людини в роках, ![]() – ємність легенів в літрах. Встановити, в якому віці ємність легенів найбільша і чому дорівнює.
– ємність легенів в літрах. Встановити, в якому віці ємність легенів найбільша і чому дорівнює.
Розв’язання
Для розв'язання даної задачі, необхідно знайти похідну за даною залежністю: 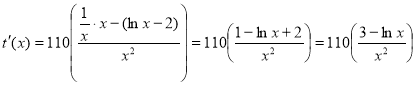 .
.
Знайдемо критичні точки: ![]() ,
, ![]() ,
, ![]() ,
,
![]() – критична точка, обчислити наближене значення
– критична точка, обчислити наближене значення ![]() років.
років.
Отже, максимальна ємність легенів людини досягається у віці 20 років. Обчислимо її значення: ![]()
![]() л.
л.
Задача 4. При вливанні глюкози протягом t хвилин у кров хворого її вміст складає ![]() . Якими будуть прирости глюкози в крові протягом
. Якими будуть прирости глюкози в крові протягом
Додаток 2
Графічний диктант
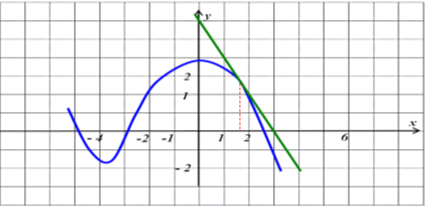
Завдання 2. На рисунку зображено графік функції ![]() і дотична до нього в точці з абсцисою
і дотична до нього в точці з абсцисою ![]() . Знайти значення похідної функції
. Знайти значення похідної функції ![]() в точці
в точці ![]()
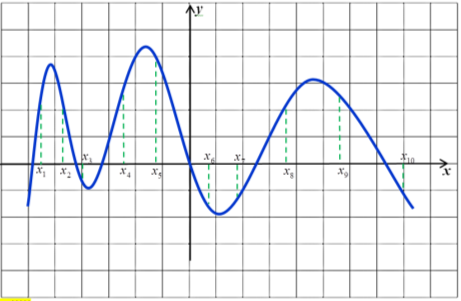
Завдання 2. На рисунку зображено графік функції ![]() . На осі абсцис відмічено десять точок. Знайти всі точки, в яких похідна функції
. На осі абсцис відмічено десять точок. Знайти всі точки, в яких похідна функції ![]() від’ємна.
від’ємна.
Завдання 3. На рисунку зображено графік похідної функції ![]() на інтервалі (-8;8). Відповісти на наступні запитання:
на інтервалі (-8;8). Відповісти на наступні запитання:
- Скільки критичних точок має функція?
- Скільки проміжків зростання має функція?
- Скільки точок екстремуму має функція?
- Укажіть кількість точок максимуму;
-
Укажіть кількість точок, де дотична паралельна прямій
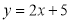 .
.
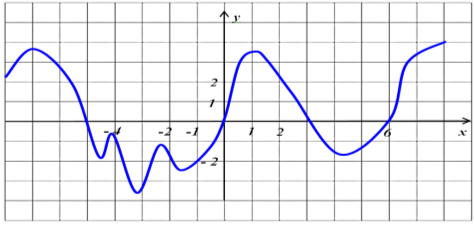
Завдання 3. Провести дослідження функції та побудувати її графік
Варіант 1 ![]() Варіант 2
Варіант 2 ![]()
Варіант 3 ![]()


про публікацію авторської розробки
Додати розробку
