Урок "Застосування визначеного інтеграла"
Узагальнити знання учнів із теми «Первісна та інтеграл»,розвивати вміння застосовування інформаційних технологій для перевірки знань учніввідповідно до сучасних вимог , активізувати взаємодію між учнями, виховувати інтерес до математики; актуалізувати досвід учнів; надати можливість стати «успішним», практично застосовувати інформаційні технології; розвивати прийоми розумової діяльності (узагальнення, аналіз, синтез, порівняння).
Державний навчальний заклад
«Нововолинський центр професійно-технічної освіти»

Панас Г.І.,
викладач математики,
спеціаліст вищої категорії,
старший викладач
Вступ
Комп’ютерні технології надають великі можливості для розвитку процесу сучасної освіти. Важливе значення має ефективне використання педагогічних програмних засобів у навчальному процесі.
У поданій методичній розробці уроку «Застосування визначеного інтеграла» акцентується увага на історії виникнення інтеграла і сферах його використання. Це є урок узагальнення і систематизації знань, який вимагає чіткої організації, високої активності і зацікавленості учнів.
Ще К.Д. Ушинський зазначав: «Дитяча природа потребує наочності». Зараз це вже не тільки схеми, таблиці і картинки, а більш близька дитячій природі гра, нехай навіть і науково-пізнавальна.
Метод інтегрального числення - один із фундаментальних математичних методів пізнання закономірностей навколишнього світу. Під час вивчення теми «Первісна і інтеграл» учні ознайомлювалися з основними ідеями інтегрального числення та його найпростішими застосуваннями. Великою є роль інтегрального числення в дослідженнях процесів і явищ реального світу: задачі на визначення закону руху тіла, гармонічні коливання, радіоактивний розпад речовин, охолодження тіла в середовищі, приріст населення, закони механіки, біологічні процеси тощо.
При вивченні теми акцентувалася увага саме на практичному використанні первісної і інтеграла.
Метою уроку є узагальнення знань учнів із теми «Первісна та інтеграл», активізація взаємодії між учнями, виховування інтересу до математики; актуалізація досвіду учнів; надання можливостей стати «успішним»; розвивання прийомів розумової діяльності (узагальнення, аналіз, синтез, порівняння), навчання самостійно працювати над творчими завданнями, пов’язувати вивчену тему із майбутньою професією .
На уроці узагальнюються знання, повторюються і закріплюються основні поняття і формули з теми, розвиваються практичні навички, вміння застосовувати набуті знання, розвивається логічне мислення.
На усіх етапах уроку використовуються активні форми навчання.
Застосовано інформаційні технології для перевірки знань учнів відповідно до сучасних вимог; впроваджено у навчальний процес елементи програми «Intel@. Навчання для майбутнього»; використано основні поняття, формули, правила, теореми. Теоретичні відомості поєднані із історичними довідками про розвиток інтегрального числення.
Для закріплення знань, навичок і умінь запропоновано завдання самостійної роботи, добірки задач та їх розв’язання , кросворд, тестові завдання.
Домашнє завдання диференційоване, передбачає підготовку до ДПА.
Особливістю даної розробки є те, що вона тісно пов’язана із професійною спрямованістю даної теми для учнів, що навчаються за професією «Слюсар з ремонту автомобілів».
Таким чином, комп’ютер – це засіб пізнання; він сприяє розвитку мотивації, комунікативних здібностей, нагромадженню фактичних знань,сприяє розвитку інформаційної грамоти. Його використання на уроці відіграє важливу роль у спостережливості, увазі, мисленні учнів. Показана Презентація дозволяє покращити запам’ятовування і засвоєння матеріалу, який вивчається.
Уроки такого типу допомагають викладачам розв’язати наступні дидактичні завдання: засвоєння базових знань з предмету, систематизація засвоєних знань, формування навиків самоконтролю, формувати мотивацію до навчання, надати методичну допомогу учням у самостійній підготовці до уроку.
Використання на уроці мультимедійних засобів сприяє формуванню у учнів уміння працювати з різною інформацією, критично до неї відноситися, розвиває логічне мислення, забезпечує інформаційну і емоційну наповнюваність уроку, сприяє підвищенню інтересу учнів до предмету, забезпечує зв'язок навчального матеріалу із реальним життям. Використання комп’ютерного тестування підвищує ефективність навчального процесу, активізує пізнавальну діяльність учнів.
Наведені приклади і задачі не є обов’язковими. Використовуючи цю розробку, викладачі математики ПТНЗ мають можливість запропонувати і використати свої варіанти задач чи завдань професійного напрямку.
Розробка уроку «Застосування визначеного інтеграла» корисна у першу чергу для викладачів математики училищ. У ній вони можуть знайти корисний матеріал і використати у своїй роботі.
Тема . Застосування визначеного інтегралу
Мета: узагальнити знання учнів із теми «Первісна та інтеграл», розвивати вміння застосовування інформаційних технологій для перевірки знань учнів відповідно до сучасних вимог , активізувати взаємодію між учнями, виховувати інтерес до математики; актуалізувати досвід учнів; надати можливість стати «успішним», практично застосовувати інформаційні технології; розвивати прийоми розумової діяльності (узагальнення, аналіз, синтез, порівняння).
Тип уроку: комплексне застосування знань та способів дій.
Обладнання :
- технічне: комп’ютери ; мультимедійний проектор;
- програмне забезпечення : педагогічний програмний засіб «Алгебра і початки аналізу» 11 клас, ОС PowerPoint;
- дидактичний матеріал: тестові завдання, завдання самостійної роботи, задачі професійної спрямованості, кросворди;
- інтерактивні технології : випереджаюче навчання, повідомлення учнів, елементи програми Intel @«Навчання для майбутнього».
Міжпредметні зв’язки : інформатика, виробниче навчання, фізика, економіка.
Очікувані результати: учні повинні
знати: - таблицю первісних елементарних функцій,
- правила знаходження первісних,
- формулу Ньютона-Лейбніца,
- таблицю інтегралів;
вміти : - знаходити первісну з використанням таблиці первісних та
правил знаходження первісних,
- застосовувати формулу Ньютона – Лейбніца до обчислення
визначеного інтеграла,
- обчислювати за допомогою інтеграла площу криволінійної
трапеції,
- застосовувати інтеграл до розв’язування задач стереометрії,
фізики, економіки, техніки.
Структура уроку
1.Організаційний момент.
2. Вступна бесіда викладача.
3. Перевірка домашнього завдання (тести, індивідуальні завдання).
4. Сприймання і усвідомлення матеріалу ( історичні повідомлення).
5. Застосування вивченого матеріалу (Презентація, розв’язування задач).
6. Закріплення вивченого ( тести «Перетягування», кросворди).
7. Підсумок уроку і оцінювання.
Характеристика уроку
Учні завершують вивчення теми «Первісна і інтеграл». Основними темами були: «Поняття первісної. Таблиця первісної. Основна властивість первісної», «Невизначений інтеграл», «Правила знаходження первісної», «Приклади, що приводять до поняття інтеграла. Означення інтеграла. Формула Ньютона-Лейбніца», «Застосування інтеграла до обчислення площ плоских фігур», «Інтеграл у фізиці та техніці».
Це урок систематизації і узагальнення знань. Його мета узагальнити і систематизувати знання учнів з теми «Первісна і інтеграл», показати зв'язок з виробничим навчанням ― слюсарною справою. На всіх етапах уроку використовуються активні форми навчання, максимально проявляється робота усіх учнів .
У навчальній групі є теоретики, дослідники, практики. Таким чином усі учні групи закріплюють набуті вміння та навичкиі отримують відповідні оцінки.
Сміливість розуму характерна для всіх математиків.
Математик не любить, коли йому про щось розповідають, він сам хоче дійти до всього.
І.Сойєр.
Хід уроку
І. Організаційний момент.
ІІ. Вступна бесіда викладача.
Сьогоднішній урок у нас буде незвичним. Ми разом продемонструємо усі свої знання, вміння, можливості.
Ви уже знаєте основні формули та правила знаходження інтегралів, вмієте їх вірно і розумно застосовувати.
Зверніть увагу на епіграф нашого уроку : Сміливість розуму характерна для
всіх математиків. Математик не любить, коли йому про щось розповідають, він сам хоче дійти до всього.
Невідомо чи станете ви великими математиками, проте у кожного із вас є велике бажання до усього доходити самим.
Отож, починаємо.
ІІІ. Перевірка домашнього завдання.
На кожному уроці , щоб він був результативним , необхідно оцінити і уміння і навички.
Першим етапом оцінювання буде перевірка отриманих раніше знань за допомогою тестів (додаток 1) і індивідуальних завдань (додаток 2).
До комп’ютерів я запрошую: _____________________________________
Інші учні отримують індивідуальні завдання на місцях – Обчислити площі криволінійних трапецій (додаток 2)
(Роздати завдання і пояснити схему виконання і оцінювання)
(В цей час звучить тиха музика _________________ )
Ми завершили роботу. Оцінки учасникам тестування виставив комп’ютер. Результати кожного етапу будуть зафіксовані у бланку оцінювання (додаток) і підсумовані у кінці уроку.
ІУ. Сприймання і усвідомлення матеріалу.
Отже, Первісна – позаду.
За нею ждуть нас інтеграли
І дифрівнянь стрункі ряди,
А потім треба йти нам далі –
Веди нас, первісна, веди!
Відкрий секрети нам науки,
Поживу дай уму й душі,
Хай вдячно нам потиснуть руки
Ньютон, і Лейбніц, і Коші.
- А що ж зробили для науки
Ви, математики - мужі.
А зараз запишемо тему уроку: « Застосування визначеного інтеграла».
На попередніх уроках ви отримали випереджаючі завдання по темі «Первісна і інтеграл».
Цікаво, що у нас вийшло…
1-й учень. Я хочу зробити повідомлення «Про походження термінів і позначень».
Про походження термінів і позначень
Історія поняття інтеграла тісно пов’язана із задачами знаходження квадратур. Задачами про квадратуру тієї чи іншої плоскої фігури математики Стародавньої Греції та Риму називали задачі, які ми нині відносимо до задач на обчислення площ. Латинське слово guadratura перекладається як «надання квадратної форми». Необхідність у спеціальному терміні пояснюється тим, що в античний час (аж до ХУІІІ ст..) ще не були достатньо розвинені звичні для нас уявлення про дійсні числа. Математики оперували їх геометричними аналогами або скалярними величинами, які не можна перемножити. Тому і задачі на знаходження площ доводилося формулювати так : «Побудувати квадрат, рівновеликий даному кругу» (ця класична задача про «про квадратуру круга» не розв’язується за допомогою циркуля і лінійки).
Символ ![]() увів Лейбніц у 1675р. Цей знак є зміненою латинською буквою (перша буква слова summa). Саме слово інтеграл увів Я.Бернуллі у 1690р. Можливо воно походить від латинського integro, яке перекладається як приводити в початковий стан, відновлювати. (Операція інтегрування «відновлює» функцію, внаслідок диференціювання якої утворено підінтегральну функцію). Можливо , походження терміна інтеграл інше: слово integer означає цілий.
увів Лейбніц у 1675р. Цей знак є зміненою латинською буквою (перша буква слова summa). Саме слово інтеграл увів Я.Бернуллі у 1690р. Можливо воно походить від латинського integro, яке перекладається як приводити в початковий стан, відновлювати. (Операція інтегрування «відновлює» функцію, внаслідок диференціювання якої утворено підінтегральну функцію). Можливо , походження терміна інтеграл інше: слово integer означає цілий.
Під час листування Й.Бернуллі і Г. Лейбніца погодилися із пропозицією Я.Бернуллі. Тоді ж, у 1696р., з’явилася й назва нової галузі математики – інтегральне числення (calculus integralis) .
Інші відомі терміни, що стосуються інтегрального числення, з’явилися значно пізніше. Назва первісна функція, що застосовується тепер, замінила більш ранню «примітивна функція», яку ввів Лагранж у 1797р. Латинське слово primitivus перекладається як «початковий». У сучасній літературі множина усіх первісних для заданої функції називається також невизначеним інтегралом.
2-й учень. Моє повідомлення пов’язане «З історією інтегрального числення»
З історії інтегрального числення
Багато значних досягнень математиків Стародавньої Греції у розв’язуванні задач на знаходження квадратур (тобто обчислення площ) плоских фігур, а також кубатур (обчислення об’ємів ) тіл пов’язані із застосуванням методу вичерпування, що запропонував Евдокс Кнідський (бл. 408-355рр. до н.е.). За допомогою цього методу Евдокс довів, що площі двох кругів відносяться, як квадрати їх діаметрів, а об’єм конуса дорівнює третині об’єму циліндра, з такою ж основою і висотою.
Цей метод удосконалив Архімед. Виведення формули площі круга в геометрії ґрунтується на ідеях Архімеда. За допомогою методу вичерпування і цілого ряду інших дотепних міркувань вчений розв’язав багато задач : дав оцінку числа π , знайшов об’єми кулі і еліпсоїда, площу сегмента параболи. Сам Архімед високо цінив ці результати: за його бажанням на могилі висікли кулю, вписану в циліндр.
Архімед передбачив багато ідей інтегрального числення. Але пройшло більш як півтори тисячі років, перш ніж ці ідеї знайшли чітке вираження і були доведені до рівня числення.
(Паралельно інший учень показує презентацію про Архімеда. Додаток 3 )

3-й учень . Я маю намір розповісти про «Застосування визначених інтегралів»
Застосування визначених інтегралів
За допомогою визначених інтегралів обчислюють площі криволінійних фігур на площині, статистичні моменти, моменти інерції, роботу сили, потенціали. Наприклад, обчислюючи роботу сили, доводиться мати справу з функціями, аргументом яких є довжина кривої, відлічувана від певної точки на кривій, - криволінійна координата. До таких функцій застосовують такий самий обчислювальний процес, що й для знаходження визначеного інтеграла як границі інтегральних сум. Але шлях інтегрування не є прямолінійним відрізком осі абсцис, а є дугою певної кривої. Такий інтеграл називають криволінійним. Інтегрування застосовують до функцій кількох змінних і інтерпретують як обчислення об’єму , тобто запроваджують подвійні, потрійні і п-кратні інтеграли. Узагальнення криволінійних інтегралів приводить до поверхневих інтегралів. Досліджують також умови, які повинна задовольняти функція, щоб до неї можна було застосувати інтегрування.
Виникнення інтегрального числення пов’язане з потребою обчислення площ і об’ємів. Уже в античній математиці для обчислення площ і об’ємів застосовували способи , схожі на обчислення визначених інтегралів. Значних успіхів у цьому досяг давньогрецький математик Архімед (ІІІ ст.. до н.е. ), який для розв’язування задач на обчислення площ і об’ємів застосовував метод вичерпування. (презентація)
Створенню інтегрального числення сприяли праці Й.Кеплера, Б.Кавальєрі, Е.Торрічеллі, Дж.Валліса , Б. Паскаля. Математики ХУІІ ст. не користувалися поняттям границі. Замість цього вони говорили про «суму нескінченно великої кількості нескінченно малих доданків». Площу криволінійної трапеції вони уявляли складеною із вертикальних відрізків довжиною f(x), яким , проте, приписували площу, що дорівнює нескінченно малій величині f(x)dx. Шукана площа подавалася у вигляді суми нескінченно великої кількості малих площ ![]() . Іноді навіть підкреслювалося, що окремі доданки цієї суми нулі, але нулі особливі, в результаті додавання нескінченної кількості яких дістаємо цілком певну додатну суму. Учитель І.Ньютона І.Барроу встановив зв'язок між диференціюванням та інтегруванням у геометричній формі, а І.Ньютон і Г.Лейбніц незалежно один від одного в кінці ХУІІ ст. розробили для цих двох операцій системи позначень і правил, вказали на зв'язок між ними. З того часу це окремий розділ математики. Метод Ньютона-Лейбніца починається заміною кривої, що обмежує площу, яку треба знайти, послідовністю ламаних, що наближається до неї , аналогічно до методу вичерпування. Операція, обернена до диференціювання, називається інтегруванням.
. Іноді навіть підкреслювалося, що окремі доданки цієї суми нулі, але нулі особливі, в результаті додавання нескінченної кількості яких дістаємо цілком певну додатну суму. Учитель І.Ньютона І.Барроу встановив зв'язок між диференціюванням та інтегруванням у геометричній формі, а І.Ньютон і Г.Лейбніц незалежно один від одного в кінці ХУІІ ст. розробили для цих двох операцій системи позначень і правил, вказали на зв'язок між ними. З того часу це окремий розділ математики. Метод Ньютона-Лейбніца починається заміною кривої, що обмежує площу, яку треба знайти, послідовністю ламаних, що наближається до неї , аналогічно до методу вичерпування. Операція, обернена до диференціювання, називається інтегруванням.
У ХУІІІ ст. розвиткові інтегрального числення найбільше сприяли праці Якоба та Йоганна Бернуллі, Ж.Лагранжа і особливо Л.Ейлера, який довів апарат інтегрального числення майже до сучасного стану.
У ХІУ ст. інтегральне числення перебудовують на рівні зрослих вимог математичної строгості О.Коші, Г.Ріман, К.М.Жордан. важливі результати належать українському математикові М.В.Остроградському (перетворення п-кратного інтеграла на (п-1)- кратний та ін.) і російському вченому П.Л.Чебишеву (умови інтегрування диференціальних біномів та ін.).
У ХХ ст. розвитку інтегрального числення особливо сприяли праці французьких математиків (А.Лебег, Е.Борель, А.Данжуа) і радянських математиків (О.Я.Хінчин, М.М.Лузін, А.М.Колмогоров).
У. Застосування вивченого матеріалу.
Звучать слова :
Спочатку було слово…
І слово було «функція»…
І для неї було введено символ…
І ототожнювали її з аналітичним виразом або формулою…
І навчилися задавати функцію графічно або у вигляді таблиці…
І далі була границя функції…
І границя породила «метод вичерпування»…
І наслідком цього методу стали площа фігури і об’єми тіл…
І знаходили це за допомогою інтеграла, тобто первісної функції…
Отже, спочатку було слово…
І слово було – ФУНКЦІЯ…
Із поняття первісної ми отримали поняття інтеграла. Що ж можна за допомогою інтеграла визначити або дослідити?
Тільки той себе вважає сильним,
Кому з математикою дружити стильно.
Без інтегралів можна прожити,
Та чи не краще все охопити?
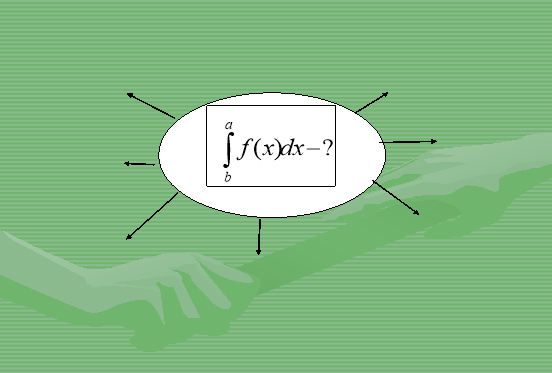
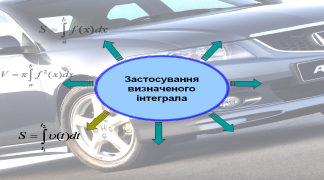
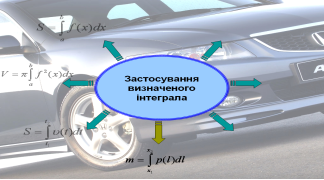
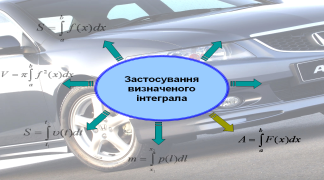
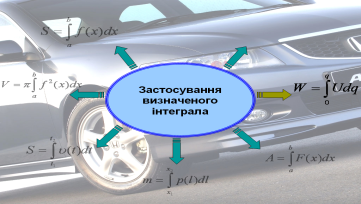
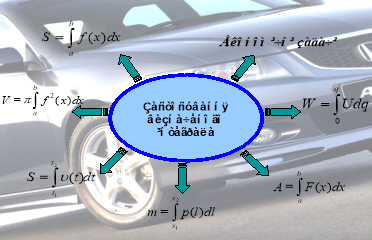
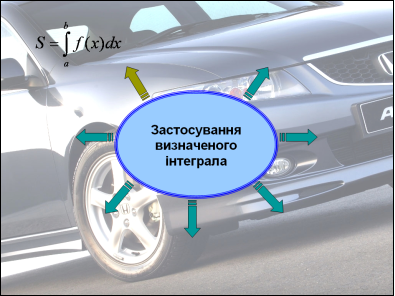
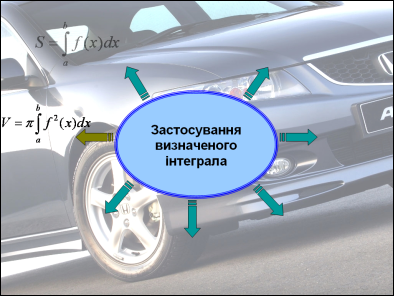
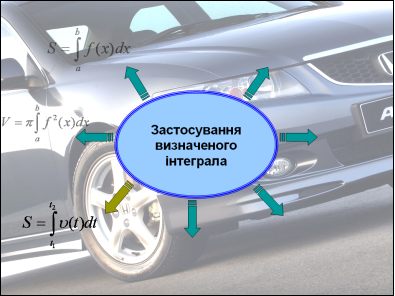
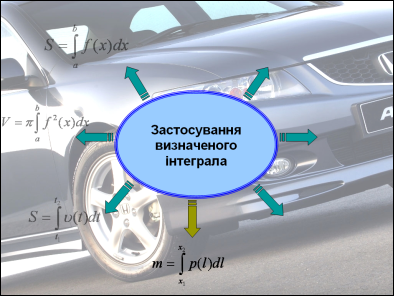
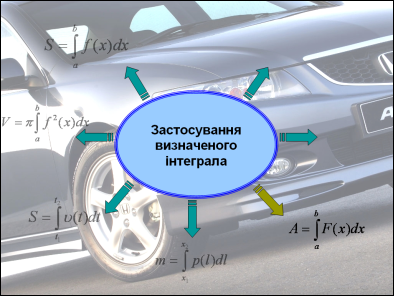
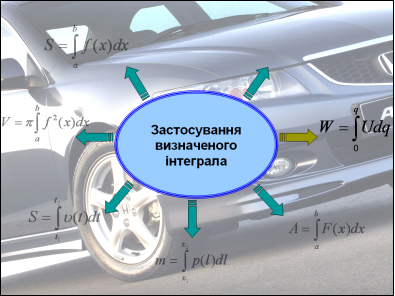
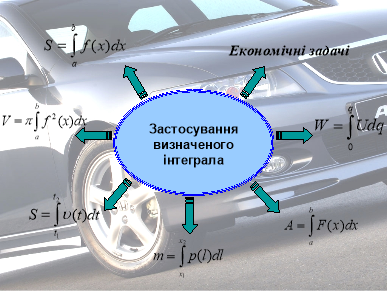
На екрані зображена схема – формула для знаходження інтегралу. Біля стрілок ви повинні записати деякі із застосувань цієї формули; усно прокоментувати конкретні використання у своїй професії.
Але спочатку запрошую до перегляду Презентації «Застосування інтеграла». (Роздати картки із схемою-формулою (проекція на екран), щоб учні по ходу пояснень її заповнювали).
![]()
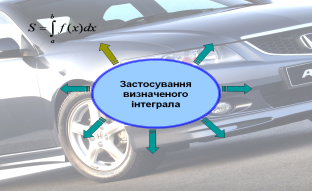
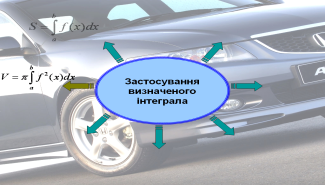
- обчислення площ (днище кузова вантажного автомобіля),
- знаходження об’ємів (бензобаку, бачка для води, цистерни),
- обчислення шляху ( шлях руху автомобіля, швидкість руху автомобіля),
- визначення маси ( бензину, електроліту),
- визначення роботи (робота насоса по подачі води на склоочисники для омивання переднього скла),
- знаходження величини заряду (знаходження ємності конденсатора),
- економічні задачі (продуктивність праці робітників автомобільного заводу).







На попередньому уроці ви отримали завдання підібрати вдома відповідні задачі, які б розкрили тему нашого уроку.
Отож, запрошую до дошки …
(Приклади задач на знаходження шляху автомобіля, обчислення маси бензину, визначення роботи для деформації ресор, обчислення енергії конденсатора (додаток 4)).

-
Швидкість руху автомобіля задано рівнянням
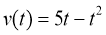 (м/с). Знайти шлях, який пройде автомобіль від початку руху до його зупинки.
(м/с). Знайти шлях, який пройде автомобіль від початку руху до його зупинки.
- У момент зупинки швидкість тіла дорівнює нулю, тобто 5t – t2=0, t(5-t)=0, t1=0; t2=5. Отже тіло зупинилось через 5с.
Шлях, який пройде тіло за цей час, обчислюється так:
![]()
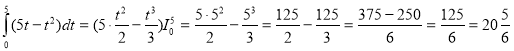 (м.)
(м.)

2. Експериментально встановлено, що залежність витрати бензину автомобіля від швидкості на 100 км шляху визначається формулою ![]() , де 30≤ v ≤110 .
, де 30≤ v ≤110 .
Визначити середню витрату бензину, якщо швидкість руху 50 – 60 км/год.
-
Середня витрата бензину становить
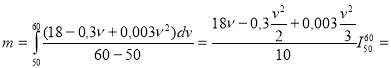
= ![]() (18*60-0,03*1800+0,003*72000-18*50+0,3*1250-0,003*41667)=
(18*60-0,03*1800+0,003*72000-18*50+0,3*1250-0,003*41667)=
= ![]() (1080-540+216-900+375-125)=10,6 (л.)
(1080-540+216-900+375-125)=10,6 (л.)
Отже, автомобіль на 100км шляху, рухаючись із швидкістю 50-60 км/год., витрачає в середньому 10,6л бензину.

- Ресора автомобіля прогинається під дією сили 1,5 . 104 Н на 1см. Яку роботу треба затратити для деформації ресори на 3 см? (Деформаційна сила пропорційна прогину ресори).
F=kx, х – прогин ресори
При х=0,01м маємо k=![]()
Тому А=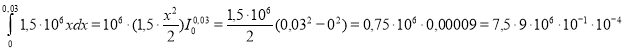 =
=
=675 Дж.

4. Знайти енергію конденсатора ємністю С= 200мкф, якщо напруга на обкладках рівна U= 1200 В.
-
200 мкф=2
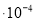 ф
ф
Напруга на конденсаторі в процесі зарядки:
U=q/c=![]() .
.
Кінцевий заряд
![]() Кл.
Кл.
Енергія зарядженого конденсатора: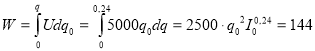 Дж.
Дж.
УІ. Закріплення вивченого.
І на завершення нашої роботи проведемо мозкову атаку на закріплення вивченого.
- Тестові завдання виконують учні , які при перевірці домашнього завдання виконували самостійну роботу.
- Кросворди (додаток 5) розв’язують учні, які при перевірці домашнього завдання розв’язували тести.
(Завдання кросворду додається. Під час виконання завдань звучить музика)
УІІ. Підсумок уроку і оцінювання.
Повернемося до епіграфу – «сам хоче дійти до всього». Що ви і довели.
Проте робота продовжується.
Домашнє завдання. Використайте збірник Завдань для ДПА : В - 16, 2.6*;
В – 17 , 2.5
В – 38, 2.5*
В - 46, 2.5.
На уроці отримали оцінки __________________________________________
І закінчити урок хочу словами англійського математика Л.Морделла :
- Ніхто не піде далеко в математиці і не стане справжнім математиком, якщо не матиме деяких необхідних рис. У ньому повинні жити Віра, Надія, і Допитливість. І найважливіша з цих рис – допитливість. Він повинен раз у раз запитувати себе : чому , як і коли – і це мусить стати головним рушієм, що приводить його в дію.
Ви побачили , що саме допитливість допомогла нам сьогодні досягнути значних результатів.
Тому я бажаю усім, щоб саме ДОПИТЛИВІСТЬ ніколи і ніде не залишала вас.
Додаток 1
Тестові завдання «Первісна і інтеграл»
1. ![]() ;
; ![]() ?
?
А) ![]() ; Б) -
; Б) -![]() ;
;
В) ![]() ; Г) -
; Г) -![]() .
.
-
Для функції
 знайти первісну, графік якої проходить через точку А(1;2).
знайти первісну, графік якої проходить через точку А(1;2).
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]() .
.
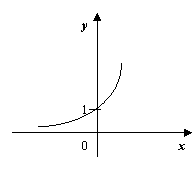
- Графік якої із даних функцій подано на рисунку.
А)![]() ; Б)
; Б) ![]() ;
;
В) ![]() ; Г)
; Г) ![]() .
.
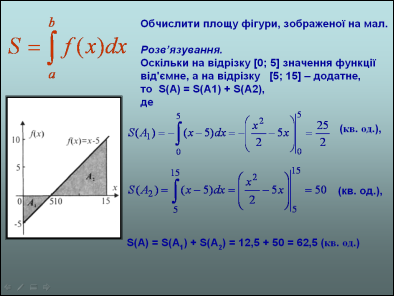
- Знайдіть площу фігури, заштрихованої на рисунку.
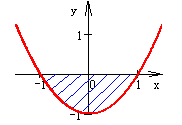
А) 1/3; Б) 1;
В) 4/3; Г) -4/3.
-
Знайти площу фігури, обмеженої лініями:
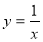 ; х=1; х=3; у=0.
; х=1; х=3; у=0.
А) 1; Б) ½; В) ln 3; Г) 3.
6. 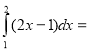 ?
?
А) 2; Б) -2; В) ½; Г) 4.
7. 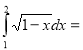 ?
?
А) 2/3; Б) -2/3; В) 1; Г) 3/2.
8. Знайти об’єм тіла, яке утворюється при обертанні навколо осі криволінійної трапеції, обмеженої лініями: ![]() ; у=0; х = 3.
; у=0; х = 3.
А) 1; Б) 1/3; В) 9; Г) 2.
Прізвище _________________________
Група ______________
Оцінка____________
Додаток 2
В-1
Обчислити площу криволінійної трапеції, обмеженої лініями:
![]()
![]() ; х=4; х=10.
; х=4; х=10.
(графіки зображати схематично)
В-2
Обчислити площу криволінійної трапеції, обмеженої лініями:
![]()
![]() ; х=2; х=0.
; х=2; х=0.
(графіки зображати схематично)
В-3
Обчислити площу криволінійної трапеції, обмеженої лініями:
![]()
![]() ; х=1; х=3.
; х=1; х=3.
(графіки зображати схематично)
В-4
Обчислити площу криволінійної трапеції, обмеженої лініями:
![]() у=0; х=2; х=3.
у=0; х=2; х=3.
(графіки зображати схематично)
В-5
Обчислити площу криволінійної трапеції, обмеженої лініями:
![]() у=0; х=0; х=2.
у=0; х=0; х=2.
(графіки зображати схематично)
В-6
Обчислити площу криволінійної трапеції, обмеженої лініями:
![]() х=2; х=3; у=0.
х=2; х=3; у=0.
(графіки зображати схематично)
Додаток 3


Додаток 4
Задачі




Кросворд на тему “Інтеграл”
Додаток 5
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
По горизонталі
3. Найпростіший прилад для вимірювання площі.
5. Сукупність усіх первісних —…
6. За допомогою інтеграла шукають…
7. Один із елементів прямокутника, який потрібен для обчислення площі.
По вертикалі
1. Метричний вимір фігури.
2. Якщо F(x)=0, то F(x)=C, де С—…
3. Якщо функція має похідну, то вона має і …
4. Будь-яке стереометричне тіло має...
Додаток 5
Презентація






Література
- Бородін О.І., Бугай А.С. Біографічний словник діячів у галузі математики. – К.: Рад. шк., 1973.
- Возняк Григорій, Возняк Ольга. Дидактичні матеріали для атестаційних робіт і тематичного контролю знань з алгебри і початків аналізу, 10 і 11 класи. – Т.: Підручники & посібники, 2001.
- Возняк Григорій, Возняк Ольга. Диференційовані дидактичні матеріали з алгебри і початків аналізу: 11 клас. – Т.: Підручники & посібники, 2000.
- Збірник завдань для державної підсумкової атестації з математики. 11 клас: У 2 кн. Кн. 2/ М.І. Бурда, О.Я. Біляніна, О.П. Вашуленко та ін. – Х.: Гімназія, 2008.
- Збірники завдань для тематичного оцінювання. Математика, 10 клас, 11 клас / Н.С. Прокопенко, А.Г. Мерзляк, В.Б. Полонський, М.С. Якір. – К.: КІМО, 2002.
- Інформаційно-практичний бюлетень «Все для вчителя», № 3-4, 2005, 2007.
- Мерзляк А.Г. та ін. Вчимося розв’язувати задачі з початків аналізу: Навч.-метод. посіб. / А.Г. Мерзляк, В.Б. Полонський, Ю.М. Рабинович, М.С. Якір. – Т.: Підручники і посібники, 2003.
- Стасюк В.Д. Практикум з розв’язування конкурсних завдань з математики. – К.: Карбон, 2006.
- Шкіль М.І., Слєпкань З.І., Дубинчук О.С. Алгебра і початки аналізу: Навч. посібник для учнів проф.-техн. навчальних закладів. – К.: Техніка, 2000.
-
+


про публікацію авторської розробки
Додати розробку
