Урок "Застосування властивостей степеня з натуральним показником"

 

 

 

 

Урок алгебри у 7 класі

на тему:

«Застосування  властивостей  степеня  з натуральним  показником»

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 Мета : формування вмінь учнів тотожно перетворювати вирази зі степенями.

 Тип уроку: урок   застосування  знань,  формування  умінь та  навичок  учнів.

Обладнання: дошка, плакат з  „алгебраїчною  ромашкою”,  таблиця  із  завданнями  уроку  для  кожного  учня,  картки  із  завданнями  для  змагання,  картки  із  текстом  самостійної  роботи.

Хід  уроку

     І. Організаційно  психологічний  етап.

Вітання  з  учнями.

•              На  сьогоднішньому  уроці  ми  маємо  навчитися  застосовувати

властивості  степеня  на  практиці.

     ІІ. Перевірка домашнього завдання, актуалізація  опорних  знань,  вмінь, постановка  мети,  мотивація. 

-  Ми  маємо  повторити  властивості  степеня  з  натуральним  показником,  маємо  навчитися  застосовувати  їх  при  розв’язуванні  різних  практичних  завдань,  але  крім  того,  ми  маємо  встигнути  перевірити  результати  своєї  навчальної  діяльності  під  час  виконання  самостійної  роботи,  бо  отримані  сьогодні  знання  знадобляться  нам  на  наступному  уроці  при  знайомстві  із  новим  для  вас  поняттям – „одночлен”.  Ми  будемо  вчитися  виконувати  різні  операції  з  одночленами,  але  цьому  неможливо  навчитися  не  знаючи  властивостей  степеня  з  натуральним  показником  і  не  навчившись  ними  користуватися.

-  Тож  до  роботи!  Вдома  кожен  з  вас  мав  навчитися  формулювати  п’ять  властивостей  степеня  з  натуральним  показником  і  записувати  їх  у  вигляді  формул.  Як  ви  впоралися  із  цією  частиною  домашнього  завдання  ми  перевіримо  так:  всі  учні  класу  виймають по одній формулі і записують цю астивість на дошці. 

 

        На  дошці:       Властивості  степеня  з  натуральним  показником:

1. a^m ∙ aⁿ = a^m+n;
2. a^m : aⁿ = a^m-n;    а ≠ 0,  m > n
3. (a^m)ⁿ = a^m∙n;
4. (ab)ⁿ = aⁿbⁿ;
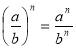5. ,  b ≠ 0

Учитель  підводить  підсумки  роботи  учнів:  узагальнює,  перевіряє,  схвалює.

-  Отже,  теорію  ви  вивчили  чудово.  Подивимось  як  ви  впорались  із  практичною  частиною  домашнього  завдання.  Я  запропонувала  вам  намалювати  „алгебраїчні  ромашки”  ( на  зворотному  боці  дошки  намальована  „алгебраїчна  ромашка”)  і,  користуючись  різними  властивостями  степеня,  на  пелюстках  цих  „ромашок”  написати  приклади,  які  б  дорівнювали  виразу  в  середині.  Давайте  разом  заповнимо  пелюстки  моєї  „алгебраїчної  ромашки”.

     На  дошці:

Учні  пропонують  свої  варіанти  прикладів,  учитель  вписує  їх  у  пелюстки  „алгебраїчної  ромашки”,  корегує  приклади  і  правильність    математичного  мовлення  учнів,  якщо  це  потрібно.

-  Свої  „ромашки”  ви  здасте  мені  на  перевірку. 

 

-  А  зараз  нам  лишається  перевірити  останнє  завдання,  яке  ви  виконували  вдома.  Кожен  з  вас  мав  в зошиті для самостійних робіт  виконати сам. Роботу ст. 14 в1. Покажіть  свої  зошити!  Тепер  обміняйтеся  завданнями  із  сусідом  по  парті!  На  виконання  роботи  1  хвилина. Відповіді записані на дошці.(1, 2, 6)  Виконавши  роботу,  не  забудьте  підписати  її  і  поверніть  автору  завдань.  Автор  прикладів  має  перевірити  правильність  виконання  роботи,  поставивши  відмітку  „+”  або  „-”  біля  розв’язку.

-  Підніміть  руки  в  кого  на  листочку  три  „+”. 

  Чудово!  Я  бачу  ви  ретельно  попрацювали  вдома:  вивчили  властивості  степеня  з  натуральним  показником  і  навчилися  користуватися  цими  властивостями  при  розв’язуванні  однокрокових  прикладів  на  безпосереднє  застосування  конкретної  властивості.  Безумовно,  це  певне  досягнення  і  успіх

ІІІ. Застосування  знань,  засвоєння  навичок  та  вмінь  на  готовому  матеріалі  (тренувальні  вправи  за  зразком,  інструкції,  завдання).

-  Пропоную  всім  розглянути  таблицю  завдань  уроку,  яка  лежить  у  кожного  на  парті.

 

Завдання  уроку
виконуються  під  керівництвом  учителя		виконується самостійно із  перевіркою  в  класі
1.  Запишіть  у  вигляді  степеня:
а)  (а2)3 ∙ (a3a4)2;б)  (х3)4 ∙ (х2х5)6;		в)  (y3y5)4 ∙ (y2)6
2.  Спростіть  вираз:
а)  (-53)7 ∙ (-52)4;  б)  (-94)2∙ (-95)3;		в)  (-43)5 ∙ (-42)3
3.  Знайдіть  значення  виразу:
а)  ;		б)
Відпочинок  (змагання) 4.  Замініть  зірочку  степенем  так,  щоб  утворилась  правильна  рівність:
-	а4 ∙ * : а13 = а2		-
5.  Порівняйте:
а)  85  та  214;		б)  1253  та  255;
6.  Розв’яжіть  рівняння:
а)  (х2х)4 = 1;		в)  (х4х3)5 – 1 =0.

 

-  Таблиця  поділяється  на  два  стовпчики  по  формах  роботи.  Перший  стовпчик  містить    завдання:  ми  докладно  розберемо  разом,  знайдемо  раціональний  розв’язок,  правильно  оформимо  завдання;  завдання  другого  стовпчику – додаткові,  вони    призначені  для  учнів,  які  працюють  самостійно.

Коментар  до  виконання  завдань:

• (завдання 1) :  відпрацьовується  правило  піднесення  степеня  до  степеня,  добуток  двох  степенів  з  однаковими  основами  і  правило  піднесення  до  степеня  добутку.

Перед  тим  як  запропонувати  самостійне  виконання  завдання  варто  навести  дітям  вислів  видатного  американського  математика  А. Ні вена: „Математику  неможна  вивчати,  спостерігаючи,  як  це  робить  сусід!” 

• (завдання 2) : важливо  запитати  в  учнів  правило  піднесення  до  степеня  від’ємного  числа.

Ймовірна  відповідь:

-  Щоб  піднести  до  степеня  від’ємне  число,  треба  піднести  до  такого  самого  степеня  модуль  цього  числа  і  перед  результатом  поставити  знак  плюс,  якщо  показник  степеня  парний,  або  мінус,  якщо  показник  степеня  непарний.

• (завдання  4) :

-  Зверніть  увагу  на  четверте  завдання! У  нас  з  вами  запланований – відпочинок.  Але  всім  відома  мудрість,  що  найкращій  відпочинок – це  зміна  праці.  Отже,  пропоную  змінити  форму  нашої  роботи  і  провести  невеличке  змагання.  Зараз  ви  об’єднаєтесь  у  дві  команди: І  ряд – І  команда,  ІІ  ряд – ІІ  команда.  Кожна  команда  отримає  своє  завдання,  яке  складається  з  чотирьох  прикладів.  Кожна  парта  працює  за  принципом: „Одна  голова – це  добре,  але  дві  краще”.  Тобто,  учні  кожної  парти  працюють  разом,  знаходять  вірне  рішення  свого  приклада  і  передають  листочок  із  завданнями  далі.  Зрозуміло,  що  переможе  команда,  яка  швидше  за  інші  і  абсолютно  вірно  виконає  завдання.  Щодо  суті  завдань:  треба замінити  зірочку  степенем  так,  щоб  утворилась  правильна  рівність.  На  старт!

ЗАВДАННЯ  ДЛЯ  ЗМАГАННЯ

І  команда 1)  а11  ∙  *  = а16; 2)   *  :  а6  = а3; 3)  ( * )2  =  а14; 4)  а3  ∙  *  = а9.

ІІ  команда 1)  х3  ∙  *  = х15; 2)   *  :  х7  = х2; 3)  ( * )3  =  х12; 4)   х3 ∙  *  = х10.

 

Учитель  підводить  підсумки  змагання:  перевіряє  правильність,  визначає  переможця,  підбадьорює  інших  учнів.

-  Мені  здається,  що  головним  досягненням  цього  змагання  є  те,  що  ви  побачили,  як  чудово  вміти  співпрацювати  в  парі,  як  чудово  відчути  радість  від  спільної  перемоги  і  як  корисно  навчитися  об’єднувати  зусилля  і  знання  задля  досягнення  успіху  своєї  команди,  чи  свого  класу,  школи,  а  може  і  всієї  країни!

 

ВІДПОВІДІ  ЗАВДАНЬ

І  команда 1)  а5; 2)  а9; 3)  а7; 4)  а6.

ІІ  команда 1)  х12; 2)  х9; 3)  х4; 4)  х7.

 

•  (завдання  5) : необхідно  пригадати  означення  степеня  (степінь – це  добуток  кількох  рівних  множників).
• (завдання  6) :  з’ясовується  питання: „Чому  дорівнює  будь-яке  число  у  першому  степені?”

Учитель  підводить  підсумки  роботи  за  таблицею  завдань:

-  Отже,  ми  виконали  з  вами  всі  заплановані  на  сьогоднішній урок  завдання.  Ми  навчилися  застосовувати  властивості  степеня  з  натуральним  показником  при  спрощенні  виразів,  під  час  обчислення  значень  виразів  та  їх  порівнянні,  при  розв’язуванні  рівнянь

IV.  Самостійна  робота  із  взаємоперевіркою.

-  Самостійну  роботу  ви  будете  виконувати  по  варіантах.  Робота  розрахована  на  5 хвилини  і  подана  у тестовій  формі.  Результати  роботи  ми  дізнаємось  відразу,  бо  зробимо  взаємоперевірку,    і  за  результатами  ви  отримаєте  домашнє  завдання.  Учні,  які  виконували  додаткові  завдання,  мають  покласти  зошити  на  край  парти,  я  перевірю  результати  вашої  індивідуальної  роботи.  (під  час  цієї  промови  учитель  роздає  учням  текст  самостійної  роботи)

САМОСТІЙНА  РОБОТА

 

Варіант  1        ________________________________________

                                                            ^{ПІ  учня}

1. Знайдіть,  які  з  даних  рівностей  неправильні:                                    ( 1 бал)

А) х⁵ ∙ х³ = х⁸;     Б) а¹² : а³ = а⁴;     В) х⁶у⁶ = (ху)¹²;     Г) (а³)² ∙ а⁴ = а¹⁰.

2. Подайте  вираз  у  вигляді  степеня  з  основою  а.                      ( 1 бал)

А) а⁸;                   Б) а³;                    В) а²;                       Г) а⁴.

3. Виконайте  піднесення  до  степеня:  (- 3х³)³.                                         ( 2 бали)

А) -9х⁹;                Б) -9х⁶;                В) -27х⁹;                 Г) 27х⁹.

4. Чому дорівнює  значення  виразу  4³ : 2⁶  ?                                              ( 2 бали)

А) 1;                     Б) 2;                    В) 32;                      Г) 4.

5. Які  з  нерівностей  правильні ?                                                                  ( 2 бали)

А) 2⁵ < 2⁶;                    Б) 2⁰ < 2;                    В) < ;              Г) 2¹ > 2.

6. Розв’яжіть  рівняння   х²х⁴ = 1.                                                                    ( 2 бали)

А) 1;                     Б) 1;                 В) -1;                      Г) немає  розв’язків.

 

                                                                                    Кількість  балів:   _______

Варіант  2       __________________________________________

                                                             ^{ПІ  учня}

1. Знайдіть,  які  з  даних  рівностей  неправильні:                                      ( 1 бал)

А) х⁶ ∙ х⁴ = х²⁴;     Б) а¹⁵ : а³ = а⁵;     В) х⁴у⁴ = (ху)⁴;      Г) (а⁷)² ∙ а⁴ = а¹⁸.

2. Подайте  вираз  у  вигляді  степеня  з  основою  а.                        ( 1 бал)

А) а⁸;                   Б) а³;                     В) а²;                       Г) а⁴.

3. Виконайте  піднесення  до  степеня:  (- 2х³)⁴.                                           ( 2 бали)

А) 8х¹²;                Б) 8х⁷;                  В) -16х¹²;                Г) 16х¹².

4. Чому дорівнює  значення  виразу  9³ : 3⁶  ?                                               ( 2 бали)

А) 0;                     Б) 3;                     В) 9;                         Г) 1.

5.  Які  з  нерівностей  правильні ?                                                                ( 2 бали)

А) < ;     Б) 3⁵ < 3⁷;            В) 3⁰ < 2;                 Г) 3¹ > 3.

6. Розв’яжіть  рівняння   х²х⁴ = 1 .                                                                 ( 2 бали)

А) 1;                     Б) 1;                  В) -1;                       Г) немає  розв’язків.

 

                                                                            Кількість  балів:   _______

 

ВІДПОВІДІ  ТЕСТІВ  (на  зворотному  боці  дошки)

Варіант  1                    Варіант  2

1. Б, В;                         1. А, Б;

2. Г;                              2. В;

3. В;                              3. Г;

4. А;                              4. Г;

5. А, Б;                          5. Б, В;

6. Б.                               6. Б.

 

Через  5  хвилини  учитель  має  призупинити  роботу  учнів,  запропонувати  їм  виконати  взаємоперевірку  і  визначити  кількість  набраних  балів.

- Підніміть  руки,  ті  учні,  які  набрали  9  або  10  балів  ( 10 - це  максимальний  результат)!  Чудово,  не  забудьте  здати  свої  роботи.  Я  бачу,  що  урок  для  вас  пройшов  не  даремно  і  ви  навчились  застосовувати  властивості  степеня.  Але  прошу  не  розгублятись  тих,  в  кого  результат  гірший,  бо  вдома  ви  повторите  властивості  степеня  і  спробуєте  виконати  аналогічні  завдання,  крім  того  на  наступних  уроках  ми  ще  не  раз  будемо  відпрацьовувати  навички  застосування  властивостей  степеня  з  натуральним  показником.

V.  Повідомлення    домашнього  завдання.

        Учитель  звертає  увагу  учнів  на  дошку:

-  Отже,  учні,  які  набрали  9,10  балів,  виконують  домашнє  завдання  ІІІ рівня.  Завдання - цікаві,  потребують  не  тільки  знань,  а  й  певної  кмітливості,  аналітичного  мислення.  Учні,  які  набрали  5 - 8  балів  мають  працювати  вдома  над  завданням  ІІ  рівня,  яке  відповідає  середньому  та  достатньому  рівню  навчальних  досягнень.  Учні,  які  набрали  1 - 4  бали,  перш  за  все  повинні  вдома проаналізувати    самостійну  роботу  (діти  роботу  не  здають),  може  ви  просто  були  неуважні  і  ваш  результат  набагато  кращій,  а  по-друге,  повторити  властивості  степеня  і  відповідні  формули.  Після  цього  ви  маєте  виконувати  домашнє  завдання  І  рівня,  яке  передбачає  безпосереднє  застосування  властивостей  степеня.

 

На  дошці:

§ 6,7 – повторити  властивості  степеня  (формули)

Виконати №319.

 

VI.  Підведення  підсумків  уроку.

-  А  зараз  нам  лишається  підвести  підсумки  роботи  на  уроці.  По-перше,  дозвольте  оцінити  роботу  окремих  учнів,  тобто  їх  рівень  навчальних  досягнень. 

Учитель  озвучує  і  коментує  оцінки  учнів,  які  активно  працювали  протягом  уроку,  враховуючи  результати  тестування,  індивідуальну  роботу,  роботу  біля  дошки  і  усні  відповіді.

-  По-друге,  пропоную  повернутися  до  мети,  яку  ми  підняли  на  початку  уроку.

Ймовірна  відповідь:

- Ні,  недостатньо  вивчити  правила  чи  формули,  треба  навчитися  ними  користуватися,  тобто  застосовувати  на  практиці!

Отже,  навчаючись  користуватися  своїми  знаннями,  ми  зростаємо  як  особистість,  ми  набуваємо  досвіду  і  впевненості  у  своїх  силах,  ми  просуваємось  вперед,  готуючись  до  дорослого  життя!