Урок "Золотий переріз"
«Золотий переріз»
Урок з математики. 6 клас
вчителя математики СЗШ № 50
Іванової Наталії Ніластіївни
спеціаліста вищої категорії
Львів - 2013
Тема: «Золотий переріз»
Мета: 1) Сформувати знання про «золотий переріз» , застосування цієї пропорції у різних видах мистецтв, діяльності людини;
2) розвивати в учнів увагу, уяву, інтуїцію, пам’ять, логічне мислення;
3) виховувати самостійність, вміння орієнтуватись у життєвих ситуаціях, зацікавленість до вивчення математики, мистецтві.
Тип уроку: засвоєння нових знань.
Метод уроку: пояснювально-ілюстративний у поєднанні з практичною роботою.
Обладнання: проектор (слайди), дидактичні картки.
Хід уроку:
- Перевірка домашнього завдання.
- Повідомлення теми, мети уроку.
- Мотивація навчальної діяльності.
Люди завжди оточували себе не лише корисними, а й красивими речами (прикрашали їх, надавали певну форму тощо). Люди не лише створювали красиві речі, вони задавались питанням: чому цей предмет гарний, він подобається, а інший, подібний на нього, не можна назвати гарним? Ще в Стародавній Греції вивчення сутності краси сформувалось у самостійну науку – естетику, де народилось уявлення про те, що основою прекрасного є гармонія. Піфагорійці прийшли до висновку, що гармонійні співвідношення частин у цілому об’єкті можна виразити за допомогою чисел. І існує одна єдина і неповторна пропорція, яка допомагає створювати гарні речі. (Слайд 1).
Слайд 1

Золотий переріз
«Геометрія володіє двома скарбами – теоремою Піфагора і «золотим перерізом»» Кеплер
- Вивчення нового матеріалу
У кінці 19 століття німецький вчений психолог Густав Теодор Фехнер проводив експеримент, якій ми зараз проведемо.
Учням пропонується серед 10 прямокутників вибрати один, який найбільше сподобався. ( Слайд 2- прямокутники Фехнера).
Слайд 2

Вчитель перевіряє прямокутник, який обрали діти (зауважуючи, що будь-який вибір є правильним і залежить лише від власних уподобань). Більшість людей обирають 7, потім 6 або 8. Саме вони відповідають так званому «золотому перерізу».
«Золотий переріз» - це поділ відрізка на дві рівні частини так, довжина всього відрізка відноситься до довжини більшої його час-тини , як довжина більшої частини до довжини меншої ![]() 1,618.
1,618.
(Слайд 3 – означення).
Вчитель звертає увагу на визначення.
Золотий переріз – це поділ відрізка на дві нерівні частини так, що довжина всього відрізка відноситься до довжини більшої його частини, як довжина більшої частини до довжини меншої ![]() .
.
Слайд 3
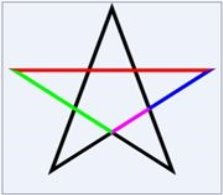
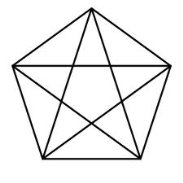
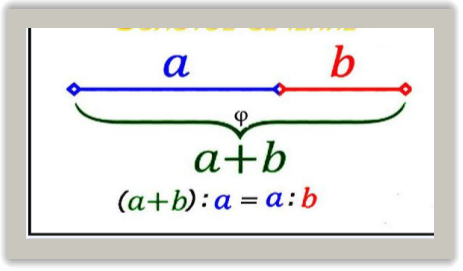
Ці відношення можна побачити на відрізках правильного п’ятикутника (відношення червоного до зеленого дорівнює відношенню зеленого до синього і дорівнює відношенню синього до червоного).
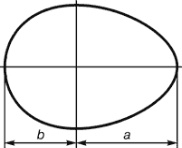
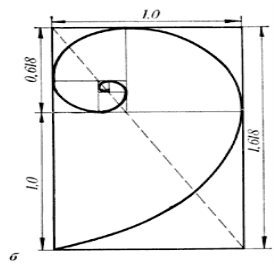
Можна з таких частин відрізка побудувати прямокутник, який називається «золотим прямокутником» (слайд 4) , а розділяючи це прямокутник таким же поділом на квадрат і прямокутник і вписуючи в квадрат коло - спіраль Архімеда.
Вчитель пропонує розглянути «золотий прямокутник» та спіраль Архімеда, розміри якої ґрунтуються на цьому же розподілі.
Слайд 4
Золотий прямокутник»
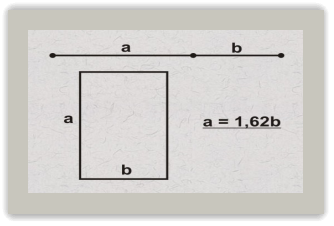
Спіраль Архімеда
Учні в зошитах малюють прямокутник із стороною b = 3см, обчислюють сторону а = 1,6b = 1.6*3 = 4.8см.
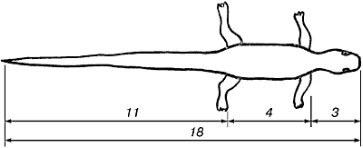
Такий розподіл цілого на частини можна зустріти і у природі (Слайд5). Вчитель пропонує розглянути приклади на деяких тваринах і рослинах.
Слайд 5
Золотий переріз у природі
Вчитель пропонує розглянути приклади у різних видах візуального мистецтвах: архітектурі, скульптурі, живопису, фотографії.
Найдавніші пам’ятки архітектури, які збереглися до нашого часу і зараз дивують своєю величчю і красотою – піраміди у Єгипті (Слайд 6).
Слайд 6
Єгипет
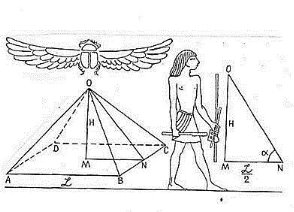

Піраміди Гізи
Виявилось, що відношення бічної грані до середини основи цих пірамід дорівнює 1,6.
І це не поодинокі випадки: Парфенон у Греції (Слайд 7),
Слайд 7
Золотий переріз в архітектурі


Парфенон в Афінах (V ст. до н.э.)
Notre Dame de Paris у Франції , (Слайд 8)
Слайд 8
Золотий переріз в архітектурі
Notre Dame de Paris (Франція)
Собор Василія Блаженного у Росії.


Собор Василія Блаженного (Москва)
Ми, львів’яни, живемо у надзвичайно гарному місті, де багато пам’яток архітектури, які побудовані у пропорціях «золотого перерізу» (Слайд 9).
Слайд 9
Архітектура Львова

Нац. Акад. театр опери та балету ім. Соломії Крушельницької


Вежа Корнякта Домініканський собор

Собор Св.Юра
Вчитель пропонує розглянути пропорції у живописі, наприклад, у відомих творах Леонардо да Вінчі : картині «Джоконда» та фресці « Таємна вечеря». (Слайд10).
Слайд 10
Золотий переріз у живопису
 Мона Ліза
Мона Ліза 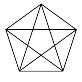
(Леонардо да Вінчі)

Таємна вечеря
Леонардо да Винчи
Розглядаючи будову людини можна побачити, що різні частини тіла знаходяться у певних відношення , серед яких можна побачити той же «золотий переріз» (Слайд 11).
Слайд 11
Пропорції людини
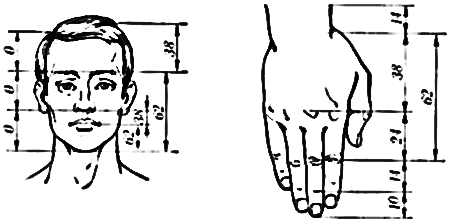
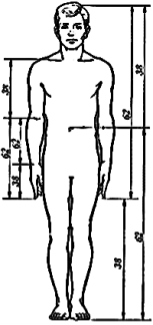
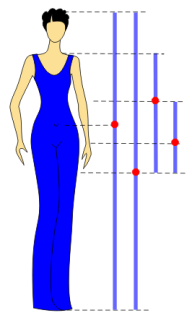
Митці Давньої Греції прагнули передати красу пропорцій людського тіла. Скульптура у Давній Греції була надзвичайно популярною. Неперевершеними зразками є, наприклад, Аполлона Бельведерського, Афіни (Слайд 12).
Слайд 12
Золотий переріз в скульптурі
 Аполлон Бельведерський
Аполлон Бельведерський
 Афіна
Афіна
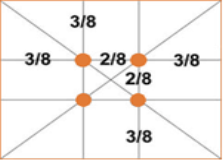
Ці знання дали поштовх на правильний ракурс, розташування об’єкта при фотографуванні. (Слайд13) В точках перехрещення прямих, які розбивають кадр на частини, що відповідають нашій пропорції найбільш концентрується увага глядача. Можна розбивати наближено на три рівні частини.
Вчитель пропонує переглянути «Золотий переріз» у фотографії.
Слайд 13
«Золотий переріз» у фотографії






5.Практична робота.
Тепер прийшов час для того, щоб подивитись як ви зрозуміли ,чи уважно ви слухали, чи добре запам’ятали. (Слайд 14).
Учням роздається практична робота, яка перевіряється і оцінюється.
(додаток 1)
- Підсумок уроку. Висновки.
«Мікрофон». Учні по черзі говорять, що їх зацікавило під час даного уроку, про що вони дізналися.
- Домашнє завдання.
Знайти приклади «золотого перерізу» в різних творах мистецтв.
Додаток 1
Практична робота.
(Практична робота)
Прізвище, ім’я _________________________________________________________
- Продовжити слова Кеплера : «Геометрія володіє двома скарбами – теоремою Піфагора і _______________________________________»
- Значення золотого перерізу наближено дорівнює __________ .
- Сторона прямокутника дорівнює 3см. Знайдіть другу його сторону, щоб це був «золотий прямокутник». Побудуйте його.
- Чи даний поділ відрізка є «золотим»? (Зробіть необхідні вимірювання і обчислення)
![]()
![]()
- Навести приклад де золотий переріз зустрічається у природі: __________________________________________________________
__________________________________________________________
- Навести приклади відомих архітектурних споруд, де можна побачити золотий переріз :_____________________________________________
____________________________________________________________
____________________________________________________________
- В яких видах мистецтва використовують золотий переріз?
_____________________________________________________________
________________________________________________________________
- Поділіть даний відрізок на відрізки,які відповідають золотому перерізу.
![]()
(Зробіть необхідні вимірювання і обчислення)
Додаток 2
Глосарій
- Гармонія - поєднання, злагодженість, взаємна відповідність якостей (предметів, явищ, частин цілого).
- Піфагор – (580 до н. е. — 500 до н. е.) — давньогрецький філософ, релігійний та політичний діяч. У 306 р. до н. е. йому, як найрозумнішому з греків, поставили пам'ятник у римському форумі.
- Леонардо да Вінчі - (15 квітня 1452— 2 травня 1519) — видатний італійський вчений, дослідник, винахідник, художник, архітектор, анатоміст, інженер, одна з найвизначніших постатей італійського Відродження.
- Фехнер - 19 квітня 1801 — † 18 листопада 1887) — німецький фізик, філософ, засновник психофізики.
-
Золотий переріз - це поділ відрізка на дві нерівні частини так, що довжина всього відрізка відноситься до довжини більшої його частини, як довжина більшої частини до довжини меншої
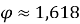 .
.
1

про публікацію авторської розробки
Додати розробку