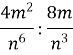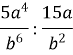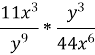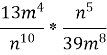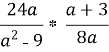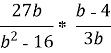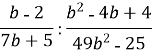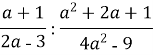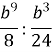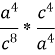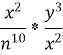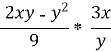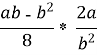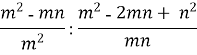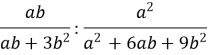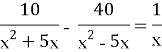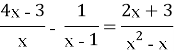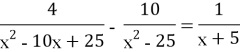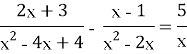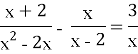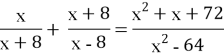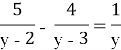Уроки "Повторення вивченого матеріалу за курс основної школи"
Підсумкове повторення вивченого матеріалу за курс основної школи
ПЛАН
Урок 1. Повторення. Тотожні перетворення раціональних виразів. Дробово-раціональні рівняння. Розв’язування текстових задач.
Урок 2. Повторення. Квадратні корені Арифметичний квадратний корінь. Перетворення виразів, що містять квадратні корені.
Урок 3. Повторення. Квадратні рівняння. Види. Способи розв’язування.
Урок 4. Повторення. Співвідношення між тригонометричними функціями одного аргумента.
Урок 5. Повторення. Елементи прикладної математики.
УРОК 1
Тема уроку : Повторення. Тотожні перетворення раціональних
виразів. Дробово-раціональні рівняння.
Розв’язування текстових задач.
Мета уроку: продовжувати формувати вміння перетворювати раціональні
вирази; повторити способи розв’язання дробово-раціональних
рівнянь, текстових задач;
формувати навички роботи в групі;
виховувати інтерес до математики.
Тип уроку: систематизація та узагальнення знань,
застосування знань та вмінь.
Наочність та обладнання: картки, індивідуальні завдання, різнокольорові
маркери.
Хід уроку
І. Організаційний етап:
- привітання,
- перевірка присутності учнів,
- перевірка готовності учнів та кабінету до уроку,
ІІ. Формулювання мети й завдань уроку , мотивація навчальної діяльності:
- оголошення теми уроку,
- формулювання разом з учнями мети та завдань уроку.
ІІІ. Мотивація навчальної діяльності:
Девіз нашого уроку – слова видатного англійського математика та фізика Ісаака Ньютона «Приклади в навчанні корисніші за правила»
IV. Актуалізація опорних знань:
1. Виконання усних вправ на швидкість обчислення «Не потрап у дроби»
Кожен учень в групі отримує картку із 16 прикладами, відповіді до яких повинен записати на окремому аркуші. Початок обчислення – за сигналом вчителя, термін - 3хв. Після сигналу вчителя – закінчили роботу.
|
Варіант 1 |
Варіант 2 |
Варіант 3 |
|||
|
1 |
0,6 *0,4 |
1 |
0,05 * 0,09 |
1 |
200 * 0,9 |
|
2 |
0,08 * 0,7 |
2 |
0,06 * 0,3 |
2 |
0,007 * 0,3 |
|
3 |
0,5 * 600 |
3 |
0,05 * 400 |
3 |
0,05 * 60 |
|
4 |
0,25 * 40 |
4 |
2,5 * 0,4 |
4 |
0,8 * 0,25 |
|
5 |
0,125 * 80 |
5 |
1,25 * 8 |
5 |
1,25 * 8 |
|
6 |
2,8 :0,7 |
6 |
0,36 :9 |
6 |
5,4 :0,9 |
|
7 |
3,2 : 8 |
7 |
4,2 : 0,7 |
7 |
3,2 : 4 |
|
8 |
0,23 |
8 |
0,022 |
8 |
0,0032 |
|
9 |
0,42 |
9 |
(-0,3)3 |
9 |
0,43 |
|
10 |
0,032 |
10 |
(-0,1)4 |
10 |
(-0,2)3 |
|
11 |
(-0,5)3 |
11 |
00,53 |
11 |
(-0,1)3 |
|
12 |
(-0,6)2 |
12 |
0,62 |
12 |
0,62 |
|
13 |
402 |
13 |
2003 |
13 |
0,032 |
|
14 |
3003 |
14 |
(-70)2 |
14 |
6002 |
|
15 |
1,22 |
15 |
1,32 |
15 |
1,62 |
|
16 |
0,142 |
16 |
0,182 |
16 |
0,0152 |
2.Повторення формул та прийомів, що використовуються для розв’язання рівнянь.
Учні працюють в групах, записують відповіді на аркушах маркерами певного кольору (у кожної групи свій колір), великими літерами, коли відповіді будуть написані, їх почеплять на дошку і презентують. За сигналом вчителя індивідуальні завдання передають по колу до повного їх заповнення.
Біля дошки учні коментують виконані завдання, виправляють помилки (якщо є), визначають переможців за кількістю правильних відповідей, записаних маркером певного кольору.
Виконати дії:
|
Завдання №1 |
Завдання №2 |
||
|
1 |
|
1 |
|
|
2 |
(- |
2 |
(- |
|
3 |
(m2 – 16n2) : |
3 |
(c2 – 25d2) : |
|
4 |
|
4 |
|
|
5 |
|
5 |
|
|
6 |
|
6 |
|
|
Завдання №3 |
Завдання №4 |
||
|
1 |
|
1 |
|
|
2 |
(- |
2 |
(- |
|
3 |
|
3 |
(d-3) : |
|
4 |
|
4 |
|
|
5 |
|
5 |
|
|
6 |
|
6 |
|
3. Актуалізація теоретичних знань (метод «Незакінчене речення»)та практичних навичок розв’язання дробово-раціональних рівнянь:
1. Рівність із невідомим значенням змінної називається … (рівняння).
2. Значення змінної, для якої рівняння перетворюється у правильну числову рівність, називається … ( коренем рівняння).
3.Розвязати рівняння означає … (знайти всі його корені або довести, що їх немає).
4. Дріб дорівнює нулю … (коли чисельник = 0, а знаменник ≠ 0).
5.ОДЗ рівняння … ( значення змінних, при яких рівняння має зміст).
6.Дробово-раціональним називається рівняння, в якому … (ліва чи права частина є дробовими виразами).
7.План-схема розв’язання дробово-раціональних рівнянь:
1) знайти спільний …(знаменник дробів, що є в рівнянні);
2)помножити обидві частини рівняння на … (спільний знаменник);
3)розв’язати … з цілими числами (рівняння);
4)перевірити корені рівняння на …(ОДЗ).
Продовжується робота в групах .Кожна група отримує плакат з рівняннями. Термін - 7-10 хв.
|
№1 |
№2 |
||
|
1 |
|
1 |
|
|
2 |
|
2 |
|
|
№3 |
№4 |
||
|
1 |
|
1 |
|
|
2 |
|
2 |
|
4. Закріплення вмінь та навичок. Розв’язування задач:
Ми доведемо -, що рівняння – це математична модель задачі, а задача - реальна життєва ситуація. Розв’язуємо задачу – готуємося до життя! Пропонуємо групам обмінятися досвідом. Скористуємося для цього «математичною каруселлю».
На 4 плакатах кожна група розв’язує по одній задачі на вибір, всього 4 задачі. Розв’язування задач в зошиті, відповідь на плакаті.
ПЛАКАТ №1 (Пропорції)
|
|
Задачі |
Група |
Відповідь |
|
1 |
Який відсотковий зміст солі в розчині, якщо 400г розчину містять 36г солі? |
|
|
|
2 |
Фермер засіяв житом 1,8 га. Це на 20%більше, ніж торік. Яку площу фермер засіяв житом минулого року? |
|
|
|
3 |
Товаркоштує 140грн. Через деякий час ціна його збільшилася на 35 грн. На скільки відсотків підвищилася ціна? |
|
|
|
4 |
Поклавши до банку 1100грн, через рік клієнт отримав відсотки 88грн. Скільки відсотків річних оплачує цей банк? |
|
|
ПЛАКАТ №2 (Лінійні рівняння)
|
|
Задачі |
Група |
Відповідь |
|
1 |
На першому складі вугілля утричі більше, ніж на другому. Скільки вугілля на кожному складі, якщо на другому на 20т менше, ніж на першому? |
|
|
|
2 |
Чи можна 59 банок консервів розмістити 3 ящики так, щоб в третьому було на 9 банок більше, ніж у першому, а в другому – на 4 банки менше, ніж у третьому? |
|
|
|
3 |
Фермер засіяв просом три поля загальною площею 1800 га. Площа першого поля становить 50% площі другого, а площа третього більша від площі першого в 3 рази. Яка площа кожного поля? |
|
|
|
4 |
Відстань від одного села до іншого пішохід проходить за 3 год, а спортсмен – за 2 год. Яка відстань між селами, якщо швидкість спортсмена на 2км/год більша від швидкості пішохода? |
|
|
ПЛАКАТ №3 (квадратні рівняння)
|
|
Задачі |
Група |
Відповідь |
|
1 |
Андрій мав набрати на комп’ютері 20 сторінок тексту за певний час. Якби він набирав щогодини на 1 сторінку більше, то виконав би завдання на 1 год швидше. Скільки сторінок планував набирати Андрій за 1 год? |
|
|
|
2 |
Катер за 1 год пройшов 20км за течією річки і 9 км проти тичїі. Знайти швидкість течії річки, якщо швидкість катера у стоячій воді 21 км/год? |
|
|
|
3 |
Різниця двох додатніх чисел дорівнює 23, а їхній добуток – 420. Знайти ці числа |
|
|
|
4 |
Відстань між містами 180км. Пасажирський потяг подолав цей шлях на 1 год швидше, ніж товарний. Знайти швидкість потягів, якщо швидкість пасажирського на 30км/год більша швидкості товарного. |
|
|
ПЛАКАТ №4 (Дробово-раціональні рівняння)
|
|
Задачі |
Група |
Відповідь |
|
1 |
Знаменник звичайного дробу більше чисельника на 3. Якщо до чисельника додати 7, а до знаменника 5, то дріб збільшиться на ½. Знайти дріб. |
|
|
|
2 |
Щоб уникнути запізнення на 1 год, поїзд на перегоні в 720км збільшив початкову швидкість на 10км/год. Яка швидкість поїзда за розкладом? |
|
|
|
3 |
Один муляр виконує роботу на 5 год швидше другого. Разом цю роботу вони виконують за 6 год. . За який час кожен з них виконує роботу? |
|
|
|
4 |
Один з бігунів пробіг відстань у 20км на 20хв швидше, ніж другий. Знайти швидкість кожного бігуна, якщо швидкість одного з них на 2км/год більша. |
|
|
Керівники груп звітують про виконану роботу.
V. Підбиття підсумків уроку.
Вчитель констатує той факт, що працюючи на уроці в групах, учні дали відповідь на 20 запитань, розв’язали 4 задачі,2 рівняння і прокоментували способи розв’язання ще 6 рівнянь і 12 задач. Це принесло чималу користь. В зошиті оцінимо свою роботу на уроці.
Оцінювання учнів.
VІ. Домашнє завдання
УРОК 2
Тема уроку : Повторення. Квадратні корені. Арифметичний
квадратний корінь. Перетворення виразів, що
містять квадратні корені.
Мета уроку: повторити означення квадратного кореня, арифметичного
квадратного кореня, закріпити навички знаходження
арифметичного квадратного кореня з добутку, дробу, степеня; повторити особливості внесення множника під знак кореня та
винесення множника з-під знака кореня; повторити виконання
тотожних перетворень з квадратними коренями;
повторити основні тотожності квадратного кореня
Тип уроку: систематизація та узагальнення знань,
застосування знань та вмінь.
Наочність та обладнання: таблиці, карточки.
Хід уроку
І. Організаційний етап:
- привітання,
- перевірка присутності учнів,
- перевірка готовності учнів та кабінету до уроку,
ІІ. Формулювання мети й завдань уроку , мотивація навчальної діяльності:
- оголошення теми уроку,
- формулювання разом з учнями мети та завдань уроку.
ІІІ. Повторення та систематизація знань:
1. Виконання усних вправ:
- скільки коренів має рівняння х2 = а?
- чим відрізняються ці корені?
- розв’язати рівняння:
х2 = 36; х2 = 81; 9х2 = 1; х2 = 0,64.
- що називають квадратним коренем із числа а?
- чи існує квадратний корінь з від’ємного числа?
- що називають арифметичним квадратним коренем із числа а?
- символ арифметичного квадратного кореня
- як за допомогою символу 
позначити обидва квадратні корені з числа а?
2. Активізація навчально-пізнавальної діяльності учнів шляхом проведення гри « Подолай перешкоди».
Завдання (вписані до «сходинок» і відповіді занесені до таблиці відповідей разом із зайвими числами) заздалегідь готують на дошці.
Грають дві команди(наприклад два ряди), третій виступає арбітром. З кожної команди до дошки виходять по одному учню, ведуть усні обчислення, (починаючи з нижньої сходинки). Одержану відповідь учень викреслює в таблиці відповідей, до дошки виходить наступний… Якщо учень виконав завдання невірно, то його повторно виконує інший член команди. Перемагає та команда, яка швидше і за меншої кількості учасників досягла фінішу .
|
Ф І Н І Ш |
|
Таблиця відповідей |
|||
|
0,1 |
-5 |
0,04 |
3,5 |
||
|
6 |
2-3 |
4 |
|
-1,5 |
|
|
0,1 |
|
4,6 |
0,3 |
-1 |
|
|
|
2 |
5 |
|
-0,9 |
|
|
( |
( |
7 |
0,49 |
-0,5 |
|
|
|
3 |
8 |
0,5 |
-0,1 |
|
|
|
|
||||
|
|
|
15,5 |
1,5 |
0 |
|
|
-5 |
-6 |
||||
|
( |
( |
400 |
2,5 |
0,03 |
|
|
|
|
||||
3. Повторення навиків виконання найпростіших тотожних перетворень виразів із коренями.
Згадати основні тотожності: 1) (
)2 =а, 2) 
= .
,а 
0, в 0,
3)
= 
, а 0,в
0, 4) 
= | а |.
4. Виконання письмових вправ (на дошці):
Обчислити:
а)
; 
; 
; 
.
б) 
; ) 
; ) 
.
в) 
; 
; 
.
г)
; 
;
.
д) Винести множник з-під знака кореня: 
; 
.
є) Внести множник під знак кореня: -5а
; 5а 
.
з) Звільнитися від ірраціональності в знаменнику:
; 
; 
; 
;
.
IV.Підбиття підсумків уроку.
Виконання тестової роботи:
І варіант
1. Обчислити: -2,6 
|
А) -13 |
Б) 13 |
В) -6,5 |
Г) 6,5 |
2. Який з наведених виразів має зміст при х
-5
|
А) |
Б) |
В) |
Г) |
3. При яких значеннях х визначена функція у=
|
А) х |
Б) х |
В) х |
Г) х |
4. Знайти значення функції у= 
в точці х0 = 4
|
А) 6 |
Б) -6 |
В) 5 |
Г) 15 |
5. Звільнитися від ірраціональності в знаменнику 
:
|
А) 2 |
Б) 3 |
В) 6 |
Г) 9 |
6.Спростити вираз (
– 1)2 + 2
|
А) 2+2 |
Б) 7 |
В) 4 |
Г) 8 |
ІІ варіант
1. Обчислити: -3,5 
|
А) 56 |
Б) -56 |
В) 14 |
Г) -14 |
2. Який з наведених виразів має зміст при х -3
|
А) |
Б) |
В) |
Г) |
3. При яких значеннях х визначена функція у=
|
А) х |
Б) х |
В) х |
Г) х |
4. Знайти значення функції у= 
в точці х0 = 8
|
А) 10 |
Б) -11 |
В) 14 |
Г) -10 |
5. Звільнитися від ірраціональності в знаменнику 
:
|
А) 2 |
Б) 3 |
В) 6 |
Г) 10 |
6.Спростити вираз (
– 
)2 -15
|
А) 2 |
Б)-2 |
В) 0 |
Г) -30 |
V. Домашнє завдання:
1. Спростити вираз:
а) 3 + 5 - 4;
б)
- 
+
;
в) (
+ ) *3;
г) 
+ 
.
2. Обчислити:
а) 
;
б) 
.
3. Скоротити дріб:
а) 
;
б) 
.
УРОК 4
Тема уроку : Повторення. Співвідношення між тригонометричними функціями одного аргументу.
Мета: повторити, систематизувати та поглибити знання, вміння перетворювати тригонометричні вирази;
формувати навички творчого застосування знань до виконання вправ ;виховувати культуру ведення записів як на дошці, так і в зошитах.
Тип уроку: комбінований
Форми роботи: колективна, групова, індивідуальна.
Методи навчання: пояснювально-ілюстративний, продуктивно-практичний.
Обладнання: презентація, опорний конспект, роздатковий матеріал, підручники.
ХІД УРОКУ
Що саме ти не вивчав би, -
ти навчаєшся для себе.
Гай Петроній
(держ.діяч Римської імперії у 4 ст.)
І. Організаційний етап
Інтерактивна вправа «Снігова куля»
Учитель. Які асоціації викликає у вас слово «урок»?
У —успіх...
Р —радість...
О — обдарованість...
К — кмітливість...
Успіхів бажаю вам сьогодні на уроці!
Робота радість хай вам принесе!
Обдарованість покажіть на кожномукроці,
Кмітливість впевненості хай додає!
II. Формулювання теми, мети і завдань уроку
III. Актуалізація опорних понять.
Тригономе́трія (від грец.τρίγονο — трикутник та μετρειν — вимірюю, тобто буквально вимірювання трикутників)
Вставити пропущене слово.
Тригономе́трія - розділ елементарної математики, що вивчає співвідношення між сторонами й кутами...(трикутників).
1. Математична естафета
1.Як називаються функції у= sinх, у = cosх?
А. Логарифмічні В. Тригонометричні
Б. Показникові Г. Обернені.
2. Яка з цих функцій парна?
А. Синус В.Тангенс
Б. Косинус Г. Котангенс
3. При якому значенні α синус і косинус мають однакові значення?
А. 30º В. 60º
Б. 90º Г. 45º
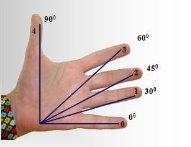
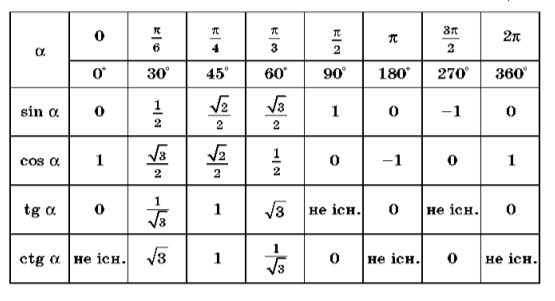
2.Завдання для майбутніх абітурієнтів: соs30º, …( робота з таблицею)
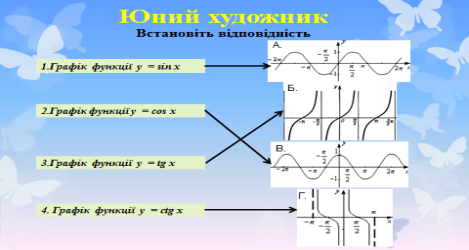
3.Дайте означення косинуса, синуса, тангенса і котангенса.
Як ми косинус знаходим
Ти спитай медузу.
- Ділим катет ми прилеглий
На гіпотенузу.
Синус нам знайти зуміє
Котик незалежний
На гіпотенузу ділить
Катет протилежний
Щоб нам тангенс заучити
Треба катети ділити.
IV.Тригонометрія в науці і в житті
Тригонометрія зустрічається не лише в математиці, але, хто би міг подумати, і в фізиці, астрономії, медицині, інших галузях:
- пружинний маятник;
- поява веселки (закон заломлення)
n1 – показник заломлення першого середовища
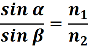n2 – показник заломлення другого середовища
α - кут падіння,
- кут заломлення світла.
- одним з основних властивостей живої природи є біоритм. Модель біоритмів може бути побудована з використанням тригонометричних функцій. Для побудови моделі біоритмів необхідно ввести
дату народження людини, дату відліку (день, місяць, рік) і кількістьднів).
- якщо на хвості риби зафіксувати точку, то можна розглянути траєкторію руху, яка нагадує косинусоїду чи синусоїду. А при плаванні тіло риби приймає форму кривої, яка нагадує графік функції y=tgx;
- при польоті птахів траєкторія крил утворює синусоїду;
- в архітектурі: ресторан в Лос-Манантіалісі, Виноробня «Бодегас Ісіос», дитяча школа в Барселоні, страхова корпорація в Лондоні;
- на танцях інколи є такий рух як хвиля, що також нагадує синусоїду чи косинусоїду.
V. Узагальнення та систематизація знань
Під час вивчення тригонометричних функцій гострого кута було доведено за теоремою Піфагора основну тригонометричну тотожність:
sin ²α + cos ²α = 1.
Як ви думаєте: що отримаємо 1- sin ²α, 1- cos ²α ?
Інші тригонометричні співвідношення мають вид:
2. tgα = 
3. ctgα = 
4. tgα
ctgα = 1 ( учні доводять користуючись формулами 2 і 3)
5. 1 + tg ²α = 
6. 1 + ctg ²α = 
.
VІ. Самостійна робота.
V. Робота з підручником.
Вправа 37 (2, 3, 5, 8) Ст.72
Відповіді: 2) ; 3) 2 
; 5); 8)
Вправа 41 (1) Ст.73
Відповідь: = 
; tgα = 
; сtgα = 
.
VІ. Підбиття підсумків уроку. Оголошення оцінок. Відповіді на запитання учнів.
Виведемо «формулу успіху», що допомагатиме боротися з труднощами не тільки в математиці, але й у реальному житті.
Успіх = несподіваність + оригінальність + дивовижна простота + фантазія + рішучий крок + здивування + краса + прагнення успіху + бажання перемогти.
Бажаю вам завжди перемагати!
Ви з математикою знайтесь, ви науку цю любіть!
Що ж, до побачення! Хай вам у житті щастить!
VІI. Домашнє завдання
Виконати завдання № 1 (1; 3), № 2, № 3 (4), № 5 (1) (Ст. 138)
VІІI. Цікавинка «Магія цифр». Загадайте будь-яке трьохцифрове число з різними цифрами, крім 0. Складіть нове число з тих самих цифр, але розміщених у зворотному порядку. Далі знайдіть різницю, і назвіть останню цифру. Після цього фокусник називає число. (Середня цифра 9, а крайні в сумі повинні дати 9)
УРОК 5
Тема уроку : Повторення. Елементи прикладної математики.
Мета уроку: узагальнити й систематизувати знання учнів з теми «Елементи прикладної математики», повторити основні типи задач на відсотки та основні статистичні поняття; закріпити уміння оперувати із статистичними даними, розв’язування прикладні задачі, задачі на відсотки та задачі на обчислення ймовірності події; розвивати самостійність, увагу, пам’ять, логічне мислення; виховувати толерантність, уміння працювати у команді, наполегливість.
Очікувані результати: учні повинні вміти розв’язувати основні задачі на відсотки, на банківські розрахунки, на обчислення ймовірності випадкової події, на знаходження центральних тенденцій вибірки.
Обладнання: підручник, роздавальний матеріал, комп’ютер, проектор, презентація.
Тип уроку: урок узагальнення й систематизації знань.
I. Організаційний етап
II. Перевірка домашнього завдання
Перевірити наявність виконаного домашнього завдання, з’ясувати питання, що виникли під час роботи.
III. Формулювання мети й завдань уроку, мотивація навчальної діяльності
Сьогодні у нас узагальнюючий урок з розділу «Елементи прикладної математики» . Епіграфом до сьогоднішнього уроку я вибрала слова М.І. Лобачевського, який сказав, що немає жодної галузі математики, якою б абстрактною вона не була, щоб вона коли-небудь не виявилась застосованою для явищ дійсного світу. І дійсно математика дуже практична річ. Сьогодні ми будемо розв’язувати прикладні задачі, повторимо необхідний для цього теоретичний матеріал Саме прикладна спрямованість математики часто допомагає нам у повсякденному житті. Активно працюйте на уроці, ставте запитання, і ви зможете краще підготуватися до ДПА.
Стародавній грецький вчений Аристотель вважав, що запитання є переходом від незнання до знань. Питання являються поштовхом для наступної діяльності. Тільки ставлячи запитання, ми можемо знайти відповіді. Тільки відчуваючи потребу, ми починаємо розв’язувати проблеми.
Питання на сьогоднішньому уроці допоможуть нам розглянути вивчені теми з усіх сторін, виділити головне, а також пов’язати його з раніше вивченим матеріалом.
IV. Актуалізація опорних знань
-
Аукціон запитань.
- Які види задач нам відомі?
- Що називається прикладною задачею?
- Що називається математичною задачею?
- Що називається математичною моделлю прикладної задачі?
- Назвіть етапи розв’язування прикладної задачі.
- Що називається математичним моделюванням?
- Чим займається наука «статистика»?
- Що таке математична статистика?
- Що таке вибірка? Навіщо використовують вибіркове спостереження?
- Що таке ранжування?
- Які є способи подання статистичних даних?
- Що таке варіанта?
- Що таке частота?
- Що називається полігоном частоти?
- Що таке центральні тенденції?
- Що таке мода вибірки?
- Що називається медіаною вибірки?
- Чи може вибірка не мати моди?
- Чи може вибірка мати дві моди?
- Сформулювати означення середнього значення n даних вибірки.
- Що таке відсоток?
- Як знайти відсоток від числа?
- Як визначити, який відсоток становить число a від числа b?
- Який вигляд має формула складних відсотків?
- Яку подію називають випадковою?
- Які бувають події?
- Що називають імовірністю випадкової події?
- Чому дорівнює ймовірність неможливої події?
- Чому дорівнює ймовірність вірогідної події?
- Звіт творчої групи про результати роботи.
Учням було потрібно обрати прикладні задачі з різних шкільних предметів і запропонувати їх математичну модель. На прикладі однієї з задач продемонструвати етапи розв’язання прикладної задачі.
V. Удосконалення вмінь
1) Робота з таблицею. Повторення і систематизація уявлень про задачі на відсоткові розрахунки та різні способи їх розв’язання
Знаходження відсотків від даного числа
Щоб знайти р % від даного числа а, достатньо це число поділити на 100 і помножити на число відсотків, тобто: 
, де 
— число, що дорівнює р % від числа 
. Або 
Знаходження числа за його відсотками
Щоб знайти невідоме число 
, р % якого становить число 
, достатньо число 
помножити на 100 і одержаний добуток поділити на р, тобто: 
Знаходження відсоткового відношення двох чисел
Щоб знайти відсоткове відношення числа до числа а, достатньо знайти їх відношення і помножити на 100 %: 
2) Практикум по розв’язуванню задач. Робота у групах
Виберіть правильну, на вашу думку, відповідь.
1. Розчин містить 4 % солі. Скільки грамів солі в 350 г розчину?
А 140 г Б 1,4 г В 0,14 г Г 14 г
2. На скільки відсотків збільшиться периметр квадрата, якщо його сторону збільшити на 80 %?
А На 20 % Б На 40 % В На 80 % Г На 144 %
3. Скільки відсотків однієї години становлять 24 хв?
А 80 % Б 24 % В 40 % Г 48 %
4. У школі 50 % учнів займаються в спортивних секціях, із них 30 %, крім того, співають у хорі. Скільки відсотків учнів одночасно займаються спортом і співають?
А 15 % Б 20 % В 25 % Г 80 %
5. Після того як ціну знизили на 20 %, товар став коштувати 248 грн. Якою була початкова ціна товару?
А 360 грн Б 1080 грн В 1240 грн Г 310 грн
6. До банку поклали 30 000 грн під 20 % річних. Скільки становитиме нарощений капітал через 2 роки?
А 43 000 грн Б 43 200 грн В 30 020 грн Г 30 040 грн
3. Додаткові завдання. Завдання для тих, хто любить думати
Маємо ряд даних: 1; 1; 4; х; 3; 9;9; 5. Знайти х, якщо мода цього ряду дорівнює 1. А. 1; Б. 3; В. 4; Г. 9
Задана вибірка: 4;4;х;4;4. Які характеристики центральної тенденції не залежать від х?
А. медіана,
Б. середнє значення,
В. Мода
Ціну на товар двічі знизили на 10%. На скільки відсотків треба підвищити нову ціну, щоб отримати початкову?
VI. Підведення підсумків уроку. Рефлексія
1. Як ви оцінюєте свою роботу на уроці?
2. Які завдання були найскладнішими?
3. Наведіть приклади застосування знань з алгебри у різних сфера діяльності людини?
VII. Домашнє завдання, інструктаж щодо його виконання
п. 17-20 повторити №963, №966, №1038
про публікацію авторської розробки
Додати розробку