Узагальнена теорема Фалеса

Тема. Узагальнена теорема Фалеса

Мета: сформувати в учнів поняття про відношення відрізків, про­порційні відрізки; сформувати свідоме розуміння учнями змісту тео­реми про пропорційні відрізки (узагальнення теореми Фалеса) та ідеї її доведення, а також можливість запису теореми у вигляді двох різних рівностей. Формувати в учнів уміння:

• відтворювати зміст вивчених на уроці тверджень;
• знаходити на рисунку пропорційні відрізки;
• записувати рівність відношень пропорційних відрізків за умовою задачі для знаходження довжин невідомих відрізків;
• використовувати теорему про пропорційні відрізки для розв'я­зування задачі на побудову четвертого пропорційного відрізка.

Тип уроку: засвоєння нових знань.

Наочність та обладнання: конспект «Теорема Фалеса».

Хід уроку

I. Організаційний етап

Оскільки урок є першим у другому розділі курсу геометрії 8 класу («Подібність трикутників. Теорема Піфагора»), то на цьому етапі уро­ку доречно буде надати учням інформацію про:

• орієнтовний план вивчення розділу;
• кількість навчальних годин, що відведено для його вивчення;
• приблизний зміст матеріалу;
• основні вимоги до знань та вмінь учнів;
• приблизний зміст завдань, що будуть винесені на контроль.

(Цю інформацію можна помістити на стенді «Довідково-інфор­маційний куточок» у кабінеті математики. З метою економії часу запро­понувати учням для самостійного ознайомлення у позаурочний час).

II. Перевірка домашнього завдання

Якщо на попередньому уроці було запропоновано учням вдома розв'язання задач контрольної роботи або корекційну роботу тощо), то правильність виконання цієї роботи вчитель перевіряє, зібравши зо­шити на перевірку (для оцінювання).

III. Формулювання мети і завдань уроку

Для розуміння учнями логіки вивчення матеріалу та з метою ство­рення мотивації навчальної діяльності учнів на уроці пропонуємо їм виконати практичну роботу.

Практична робота

1. Виконайте зображення довільного відрізка АВ . За допомогою цир­куля та лінійки поділіть відрізок АВ на дві частини у відношен­ні 2 : 3. (Точку поділу позначте літерою С). (Зауваження: під час виконання побудови використовуємо теорему Фалеса та алгоритм розв'язання задачі на поділ даного відрізка на п рівних частин.)
2. Виміряйте довжини всіх відрізків ( АВ , АС , СВ , AY , АХ , XY), що утвори­лися на рисунку І.
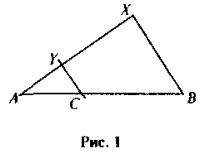3. Обчисліть значення часток: АС : ВС ; АС : АВ ; AY : XY; AY : АХ. Порівняй­те здобуті числа. Що ви помітили? Чи можете ви пояснити здобуті результа­ти?

 Виконуючи побудови, що відповідають умові задачі 1, учні дістають конфігурацію, подібну до тієї, що зображена на рис. 1.

Після виконання вимірювань та обчислень відповідно до умов за­вдань 2 і 3 учні мають помітити, що, незалежно від довжини відрізка АВ та градусної міри кута ХАВ і незважаючи на неточність вимірю­вань, серед здобутих значень часток довжин утворених відрізків є рів­ні числа, існування яких учні не можуть пояснити. Вчитель пропонує учням порівняти рис.1 із рисунком до теореми Фалеса та знайти од­накові й відмінні риси. Після виконання цієї дії учні мають поміти­ти, що, незважаючи на певну схожість (паралельні прямі перетина­ють сторони кута), випадок на рис. 1 не відповідає повністю умові те­ореми Фалеса. Таким чином формулюється проблема. Існує необхід­ність узагальнення теореми Фалеса для випадку, коли паралельні пря­мі перетинають сторони кута, відтинаючи на одній зі сторін довіль­ні відрізки, а також вираження залежності між здобутими відрізками в алгебраїчній формі. Розв'язування поставленої проблеми є основою метою цього уроку.

IV. Актуалізація опорних знань

Для успішного засвоєння учнями змісту понять «відношення відрізків», «пропорційні відрізки», змісту теореми про пропорційні відрізки (узагальнення теореми Фалеса) та ідеї її доведення, а також розуміння учнями можливості запису теореми у вигляді двох різних рівностей учням слід активізувати знання і вміння щодо означення та властивостей пропорції; змісту теореми Фалеса.

Виконання усних вправ

1. Серед записів: 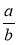, ab, a : b, а – b, а + b вибрати ті, які можна на­звати відношенням чисел а і b . Що може показувати це відношення?
2. Як називається запис 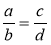? Як називаються числа а , b , с, d у цьому запису?
3. Відомо, що рівність 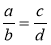є правильною. Які із запропонованих нижче рівностей є правильними? Чому?

а) ad = bс; b) ; в) ; г) ; д) .

4. а) АК : KB = 2 : 3 (рис. 2). Знайдіть: АК : АВ; ВК : АК; ВК : АВ;

б) ВК : АВ = т : п. Знайдіть АК : ВК; АК : АВ.

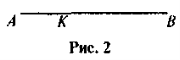
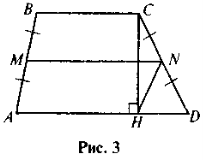
5. Знайдіть NH (рис. 3), якщо АВ = 10.

V. Засвоєння знань

План вивчення нового матеріалу

1. Уявлення про зміст понять «відношення відрізків»; «пропорційні відрізки».
2. Теорема про пропорційні відрізки (формулювання та ідея доведення).
3. Побудова четвертого пропорційного відрізка.

 Як показує досвід, труднощі сприйняття змісту, а звідси застосуван­ня узагальненої теореми Фалеса, виникають тому, що учні не розуміють змісту поняття «пропорційні відрізки». Отже, вивчення но­вого матеріалу слід розпочинати із формування свідомого розумін­ня учнями поняття пропорційних відрізків із наступним закріплен­ням його змісту на прикладах.

За такого способу вивчення матеріалу формулювання теореми про пропорційні відрізки є простим узагальненням результатів практичної роботи, тому, перш ніж формулювати твердження теореми, учитель може запропонувати учням самостійно скласти узагальнене твердження (виходячи із рівностей, які учні здобули під час виконання практичної роботи). Вчителю слід наголосити на тому, що виконана побудова не є доведенням твердження (це лише ілюстрація теореми). Учні мають розуміти, що складене твердження має бути доведеним. Оскільки строге математичне доведення узагальненої теореми Фалеса є досить складним для учнів 8 класу, то надається лише ідея доведення твердження теореми про пропорційні відрізки із посиланням на доведену раніше теорему Фалеса. Зауважимо, що, на відміну від традиційного підручника, у новому підручнику формулюється та доводиться твердження для відрізків, які послідовно розташовані на кожній зі сторін кута (за такого підходу до формулювання теореми посилання на теорему Фалеса стає більш зрозумілим).

Що стосується пропорційності відрізків, які мають спільний кінець у вершині кута, то в новому підручнику досить оригінально доведено цей факт через застосування до раніше доведеного твердження однієї із властивостей пропорції.

Після опрацювання поняття пропорційних відрізків та форму­лювання і доведення теореми про пропорційні відрізки бажано на прикладах закріпити шляхом складання відповідних пропорцій за готовими рисунками розуміння учнями змісту теореми.

Якщо учні добре засвоїли теоретичний матеріал, а також демон­струють розуміння змісту теореми та вміння застосовувати його на прикладах, можна на цьому уроці вивчити схему розв'язання базової задачі на побудову четвертого пропорційного відрізка.

VI. Закріплення знань, формування первинних умінь

Виконання письмових вправ

1. Визначте, чи є відрізки завдовжки а і b пропорційними відрізкам с і d , якщо:

а) а = 8 см, b = 24 см, с = 7 см, d = 12 см;

б) а = 9 см, b = 14 см, с = 7 см, d = 18 см.

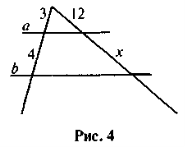
2. За даними рисунка 4 знайдіть х , якщо а || b .

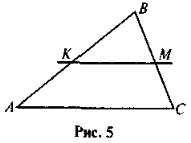
3. Пряма  KM   паралельна стороні  АС  трикутника ABC  (рис. 5). Знайдіть відрізок MС , якщо АК = 2 см, KB = 6 см, ВМ = 9 см.
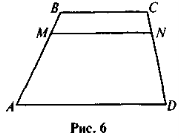
4. Пряма MN паралельна основам трапеції ABCD (рис. 6). Знайдіть сторону CD, якщо AM : AB = 4 : 5, CN = 3 см.

5. Дано відрізки а , b , с. Побудуйте відрізки: 1) 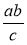; 2) .
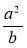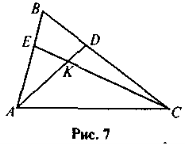
6. На рис. 7 BE : ЕА = 4 : 6, BD : DC = 6 : 7. Знайдіть відношення СК : КЕ .

VII. Підсумки уроку

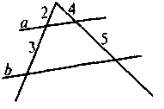
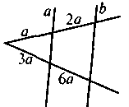
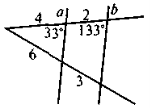
На якому з наведених рисунків допущено помилку в зображенні паралельних прямих а і b ?

VIII. Домашнє завдання

Вивчити теоретичний матеріал.

Розв'язати задачі.

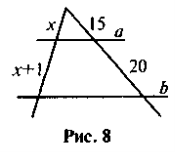
1. За даними рисунка 8 знайдіть х , якщо а || b.
2. Пряма KM паралельна стороні АС трикут­ника ABC (рис. 5). Знайдіть відрізок МС, якщо АК : KB = 2 : 3, ВС = 10 см.
3. Пряма   MN   паралельна основам трапе­ції ABCD  (рис. 6). Знайдіть сторону АВ , якщо AM : ND = 3 : 2, CN = 2 см, AM = 9 см.

4*. Дано відрізки а , b , c. Побудуйте відрізки: а) ; б) .