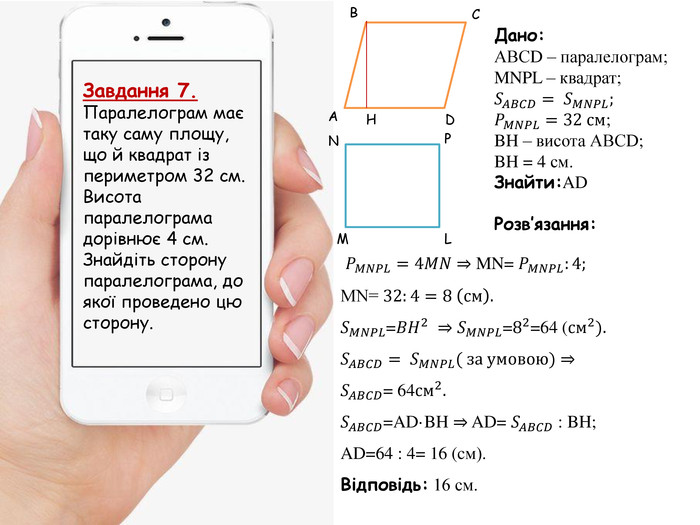
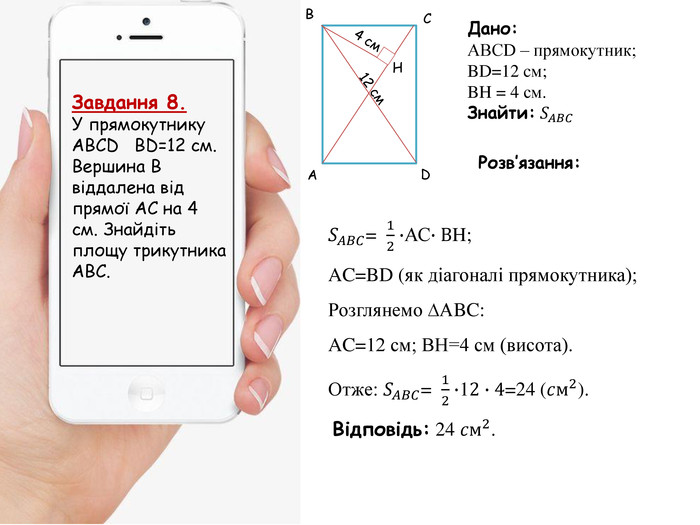
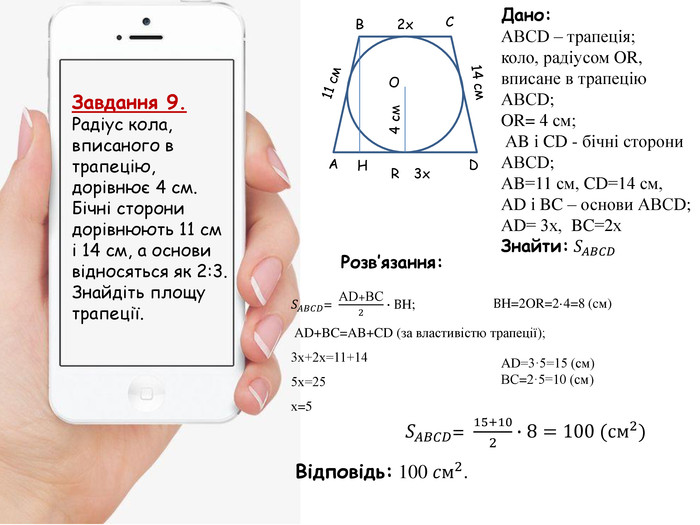
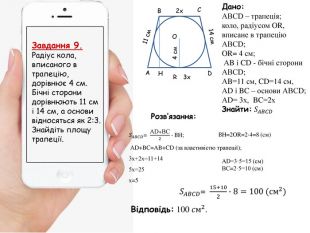
Узагальнення та систематизація знань умінь та навичок з теми "Многокутники. Площі многокутників"
Про матеріал
Узагальнення та систематизація знань умінь та навичок з теми "Многокутники. Площі многокутників" Перегляд файлу
Зміст слайдів
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку