V. Планіметрія. Частина 4. Чотирикутники

Про матеріал

Посібник призначений для підготовки учнів загальноосвітніх навчальних закладів та абітурієнтів до зовнішнього незалежного оцінювання з математики. Його укладено до чинної програми та чинних навчальних програм з математики. Метою посібника є надання практичної допомоги учням у підготовці до ЗНО та ДПА

Перегляд файлу

Чотирикутники.

(2009)19. Гострий кут паралелограма дорівнює , а його сторони – см і см. Обчисліть довжину меншої діагоналі паралелограма.

А	Б	В	Г	Д
см	см	см	см	см

Відповідь: Д.

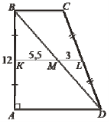
(2009)22. У трапеції , см (див. рисунок). Діагональ ділить середню лінію трапеції на відрізки і , причому см і см. Обчисліть периметр трапеції (у см).

Відповідь: .

(2010)8. Сума градусних мір двох кутів паралелограма дорівнює . Знайдіть градусну міру більшого кута паралелограма.

А	Б	В	Г	Д

Відповідь: В.

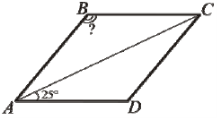
(2010)2. На рисунку зображено ромб . Знайдіть градусну міру кута , якщо .

А	Б	В	Г	Д

Відповідь: Б.

(2012)18. У прямокутнику , . Через точки і , що належать сторонам і відповідно, проведено пряму, паралельну . Знайдіть довжину більшої сторони трикутника , якщо .

А	Б	В	Г	Д

Відповідь: Г.

(2012)8. Укажіть хибне твердження.

А	Протилежні сторони паралелограма рівні.
Б	Сума двох кутів паралелограма, прилеглих до однієї сторони, дорівнює .
В	Діагоналі паралелограма точкою перетину діляться навпіл.
Г	Площа паралелограма дорівнює добутку двох його сусідніх сторін на синус кута між ними.
Д	Площа паралелограма дорівнює половині добутку його сторони на висоту, проведену до цієї сторони.

Відповідь: Д.

(2012)28. Бісектриса кута прямокутника перетинає його більшу сторону в точці . Визначте радіус кола (у см), описаного навколо прямокутника, якщо см, см.

Відповідь: .

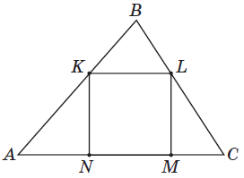
(2013)20. У трикутник вписано квадрат (див. рисунок). Висота цього трикутника, проведена до сторони , дорівнює см. Знайдіть периметр квадрата, якщо см.

А	Б	В	Г	Д
см	см	см	см	см

Відповідь: Г.

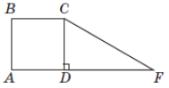
(2014)23. На рисунку зображено квадрат зі стороною см та прямокутний трикутник , гіпотенуза якого дорівнює см. Фігури лежать в одній площині. Установіть відповідність між початком речення (1 – 4) та його закінченням (А – Д) так, щоб утворилося правильне твердження.

Початок речення		Закінчення речення
1	Довжина катета трикутника дорівнює	А	см.
2	Довжина радіуса кола, описаного навколо квадрата , дорівнює	Б	см.
3	Відстань від точки до прямої дорівнює	В	см.
4	Відстань від точки до прямої дорівнює	Г	см.
		Д	см.

Відповідь: 1 – Г; 2 – Б; 3 – А; 4 – В.

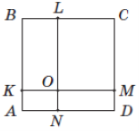
(2014)22. На сторонах квадрата задано точки , , і так, що , (див. рисунок). Відрізки і перетинаються в точці . , , . До кожного початку речення (1 – 4) доберіть його закінчення (А – Д) так, щоб утворилося правильне твердження.

Початок речення		Закінчення речення
1	Довжина відрізка дорівнює	А
2	Радіус кола, описаного навколо прямокутника , дорівнює	Б
3	Довжина середньої лінії трапеції дорівнює	В
4	Довжина відрізка , де – точка перетину бісектриси кута зі стороною , дорівнює	Г
		Д

Відповідь: 1 – А; 2 – Б; 3 – Г; 4 – В.

(2015)12. На діагоналі квадрата задано точку, відстань від якої до сторін і дорівнює см і см відповідно. Визначте периметр квадрата .

А	Б	В	Г	Д
см	см	см	см	см

Відповідь: В.

(2015)26. З вершини тупого кута паралелограма опущено перпендикуляр на сторону . Коло з центром у точці проходить через вершину та перетинає сторону в точці . Відомо, що см, см, см.

1. Визначте периметр паралелограма (у см).

2. Обчисліть довжину діагоналі (у см).

Відповідь: 1. ; 2. .

1. Визначте периметр паралелограма (у см).

2. Обчисліть довжину діагоналі (у см).

Відповідь: 1. ; 2. .

1. Визначте периметр паралелограма (у см).

2. Обчисліть довжину діагоналі (у см).

Відповідь: 1. ; 2. .

(2015)27. У прямокутній трапеції проведено середню лінію (див. рисунок). см, см, . Визначте довжину сторони (у см).

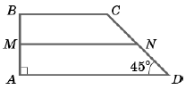
Відповідь: .

(2015)28. У прямокутній трапеції проведено середню лінію (див. рисунок). см, см, . Визначте довжину сторони (у см).

Відповідь: .

(2016)26. На рисунку зображено квадрат , сторона якого дорівнює . На сторонах і квадрата вибрано точки і так, що , .

1. Визначте відстань між серединами відрізків і .

2. Обчисліть довжину відрізка .

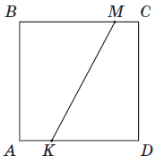
Відповідь: 1. ; 2. .

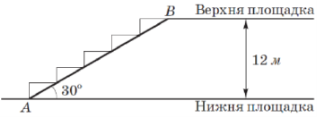
(2016)13. Нижня й верхня площадки ескалатора лежать у паралельних площинах, відстань між якими становить м (див. рисунок). Кут нахилу ескалатора до площини нижньої площадки дорівнює . Визначте довжину ескалатора .

А	Б	В	Г	Д
м	м	м	м	м

Відповідь: Б.

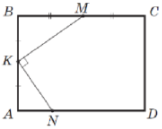
(2016)23. У прямокутнику см, см (див. рисунок). На сторонах , і цього прямокутника вибрано точки , і так, що , , . До кожного початку речення (1 – 4) доберіть його закінчення (А – Д) так, щоб утворилося правильне твердження.

Початок речення		Закінчення речення
1	Відстань від середини відрізка до сторони дорівнює	А	см.
2	Відстань від точки перетину діагоналей прямокутника до точки дорівнює	Б	см.
3	Довжина відрізка дорівнює	В	см.
4	Довжина відрізка дорівнює	Г	см.
		Д	см.

Відповідь: 1 – А; 2 – В; 3 – Б; 4 – Г.

(2017)11. Довжина сторони ромба дорівнює см. Визначте довжину більшої діагоналі цього ромба, якщо його тупий кут дорівнює .

А	Б	В	Г	Д
см	см	см	см	см

Відповідь: Г.

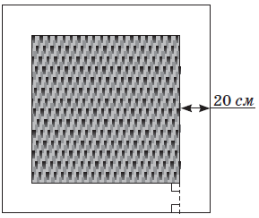
(2017)14. Підлога кімнати має форму квадрата. На ній лежить квадратний килим, кожна сторона якого віддалена від найближчої стіни кімнати на см (див. рисунок). Визначте периметр килиму, периметр підлоги дорівнює м. Наявністю плінтусів на підлозі знехтуйте.

А	Б	В	Г	Д
м	м	м	м	м

Відповідь: Г.

(2018)13. У паралелограмі на стороні вибрано точку . Діагональ і відрізок перетинаються в точці . Визначте довжину сторони , якщо см, см, см.

А	Б	В	Г	Д
см	см	см	см	см

Відповідь: Б.

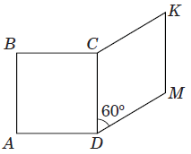
(2018)23. На рисунку зображено квадрат і ромб , які лежать в одній площині. Периметр ромба дорівнює см, а його гострий кут – . До кожного початку речення (1 – 4) доберіть його закінчення (А – Д) так, щоб утворилося правильне твердження.

Початок речення		Закінчення речення
1	Довжина сторони квадрата дорівнює	А	см.
2	Довжина більшої діагоналі ромба дорівнює	Б	см.
3	Відстань від точки до сторони дорівнює	В	см.
4	Відстань від точки до прямої дорівнює	Г	см.
		Д	см.