V. Планіметрія. Частина 6. Геометричні величини та їх вимірювання

Про матеріал

Посібник призначений для підготовки учнів загальноосвітніх навчальних закладів та абітурієнтів до зовнішнього незалежного оцінювання з математики. Його укладено до чинної програми та чинних навчальних програм з математики. Метою посібника є надання практичної допомоги учням у підготовці до ЗНО та ДПА

Перегляд файлу

Геометричні величини та їх вимірювання.

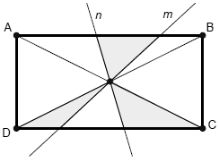
(2006)18. У прямокутнику прямі і проходять через точку перетину діагоналей. Площа фігури, що складається з трьох зафарбованих трикутників, дорівнює см². Обчисліть площу прямокутника .

А	Б	В	Г	Д
см²	см²	см²	см²	см²

Відповідь: Д.

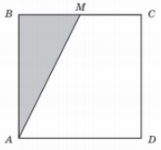
(2007)18. Точка – середина сторони квадрата . Площа зафарбованої частини дорівнює см². Знайдіть площу всього квадрата.

А	Б	В	Г	Д
см²	см²	см²	см²	см²

Відповідь: В.

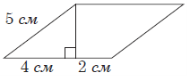
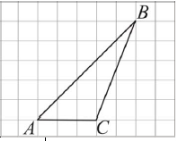
(2010)16. На папері у клітинку зображено трикутник , вершини якого збігаються з вершинами клітинок (див. рисунок). Знайдіть площу трикутника , якщо кожна клітинка є квадратом зі стороною завдовжки см.

А	Б	В	Г	Д
см²	см²	см²	см²	см²

Відповідь: Г.

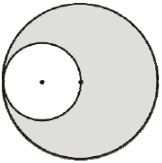
(2010)33. Два кола дотикаються, причому менше з кіл проходить через центр більшого кола (див. рисунок). Знайдіть площу зафарбованої фігури (у см²), якщо менше з кіл обмежує круг площею см².

Відповідь: .

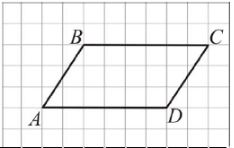
(2010)15. На папері у клітинку зображено паралелограм , вершини якого збігаються з вершинами клітинок (див. рисунок). Знайдіть площу паралелограма , якщо кожна клітинка є квадратом зі стороною завдовжки см.

А	Б	В	Г	Д
см²	см²	см²	см²	см²

Відповідь: Г.

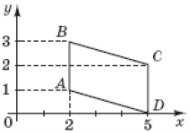
(2011)15. Обчисліть площу чотирикутника (див. рисунок), сторони і якого паралельні вісі .

А	Б	В	Г	Д

Відповідь: Г.

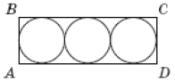
(2011)19. У прямокутник вписано три круги одного й того самого радіуса (див. рисунок). Визначте довжину сторони , якщо загальна площа кругів дорівнює .

А	Б	В	Г	Д

Відповідь: В.

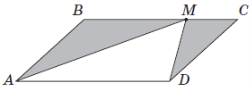
(2012)16. На рисунку зображено паралелограм , площа якого дорівнює см². Точка належить стороні . Визначте площу фігури, що складається з двох зафарбованих трикутників.

А	Б	В	Г	Д
см²	см²	см²	см²	см²

Відповідь: Г.

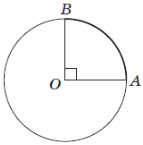
(2012)4. На рисунку зображено коло з центром в точці , довжина якого дорівнює см. Визначте довжину меншої дуги кола, якщо .

А	Б	В	Г	Д
см	см	см	см	см

Відповідь: В.

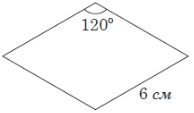
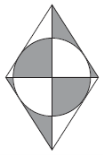
(2012)14. На рисунку зображено ромб, площа якого дорівнює см². У ромб вписано коло. Визначте площу зафарбованої фігури.

А	Б	В	Г	Д
см²	см²	см²	см²	см²

Відповідь: В.

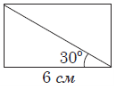
(2013)15. Менша сторона прямокутника дорівнює м і утворює з його діагоналлю кут . Середини всіх сторін прямокутника послідовно сполучено. Знайдіть площу утвореного чотирикутника.

А	Б	В	Г	Д
м²	м²	м²	м²	м²

Відповідь: Б.

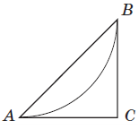
(2013)30. План паркової зони, обмеженої трикутником , зображено на рисунку. Дуга – велосипедна доріжка. Відомо, що дуга є четвертою частиною кола радіуса км. і – дотичні до цього кола ( і – точки дотику). Обчисліть площу зображеної на плані паркової зони (у км²).

Відповідь: .

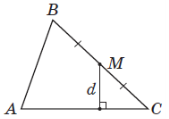
(2013)16. У трикутнику точка – середина сторони , см (див. рисунок). Знайдіть відстань від точки до сторони , якщо площа трикутника дорівнює см².

А	Б	В	Г	Д
см	см	см	см	см

Відповідь: В.

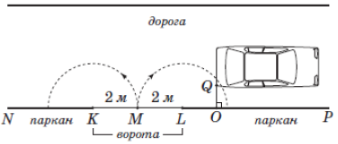
(2014)20. Автомобіль рухався по дорозі паралельно паркану і зупинився біля закритих воріт так, як зображено на рисунку. Відомо, що розмах стулки воріт становить м, м. Укажіть найменшу з наведених довжину відрізка , при якій стулка не зачепить автомобіль за умови повного відкривання воріт.

Уважайте, що ворота перпендикулярні до площини дороги і мають прямокутну форму. Товщиною стулок знехтуйте.

А	Б	В	Г	Д
м	м	м	м	м

Відповідь: В.

(2014)26. На стороні паралелограма як на діаметрі побудовано півколо так, що воно дотикається до сторони в точці . Довжина дуги дорівнює см.

1. Обчисліть (у см) довжину радіуса цього півкола.

2. Обчисліть площу паралелограма (у см²).

Відповідь: 1. ; 2 .

1. Обчисліть (у см) довжину радіуса цього півкола.

2. Обчисліть площу паралелограма (у см²).

Відповідь: 1. ; 2. .

1. Обчисліть (у см) довжину радіуса цього півкола.

2. Обчисліть площу паралелограма (у см²).

Відповідь: 1. ; 2 .

(2014)31. Діагональ рівнобічної трапеції є бісектрисою її гострого кута і ділить середню лінію трапеції на відрізки довжиною см і см. Обчисліть (у см²) площу трапеції.

Відповідь: .

(2014)25. У ромбі з вершини тупого кута до сторони проведено перпендикуляр . см, см.

1. Визначте довжину перпендикуляра (у см).

2. Обчисліть площу ромба (у см²).

Відповідь: 1. ; 2. .

(2014)25. У ромбі з вершини тупого кута до сторони проведено перпендикуляр . см, см.

1. Визначте довжину перпендикуляра (у см).

2. Обчисліть площу ромба (у см²).

Відповідь: 1. ; 2. .

(2014)25. У ромбі з вершини тупого кута до сторони проведено перпендикуляр . см, см.

1. Визначте довжину перпендикуляра (у см).

2. Обчисліть площу ромба (у см²).

Відповідь: 1. ; 2. .

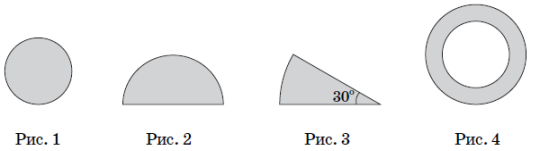
(2015)23. Установіть відповідність між геометричною фігурою (1 – 4) та її площею (А – Д).

Геометрична фігура		Площа геометричної фігури
1	круг радіуса см (рис. )	А	см²
2	півкруг радіуса см (рис. )	Б	см²
3	сектор радіуса см з градусною мірою центрального кута (рис. )	В	см²
4	кільце, обмежене колами радіусів см і см (рис. )	Г	см²
		Д	см²

Відповідь: 1 – Б; 2 – В; 3 – А; 4 – Г.

(2015)35. У прямокутному трикутнику точка є серединою гіпотенузи , довжина якої дорівнює см. Точка віддалена від вершин і на см, а від сторони – на см. З точки на катет опущено перпендикуляр , точка належить відрізку .

1. Доведіть, що чотирикутник є трапецією.

2. Визначте площу трапеції .

Відповідь: 2. см².

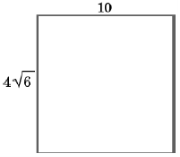
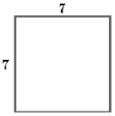
(2015)21. Установіть відповідність між твердженням (1 – 4) та зображеним на рисунку прямокутником (А – Д), для якого це твердження є правильним.

Твердження		Прямокутник
1	площа прямокутника дорівнює	А
2	периметр прямокутника дорівнює	Б
3	кут між діагоналями прямокутника дорівнює	В
4	діагональ прямокутника дорівнює	Г
		Д

Відповідь: 1 – В; 2 – А; 3 – Б; 4 – Г.

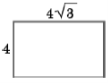
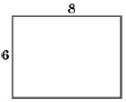
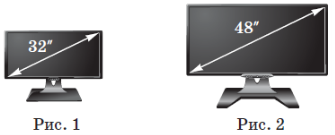
(2016)14. Екрани телевізорів, зображених на рис. і , мають форму прямокутників, відповідні сторони яких пропорційні. Діагоналі екранів цих телевізорів дорівнюють відповідно дюйма і дюймів. Визначте, у скільки разів площа екрана телевізора, зображеного на рис. , більша за площу екрана телевізора, зображеного на рис. .

А	Б	В	Г	Д

Відповідь: Д.

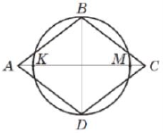
(2016)26. На рисунку зображено ромб та коло, побудоване на меншій діагоналі як на діаметрі. Довжина кола дорівнює . Це коло ділить діагональ на три відрізки , та , довжини яких відносяться як .

1. Обчисліть довжину діагоналі .

2. Визначте площу ромба .

Відповідь: 1. ; 2. .

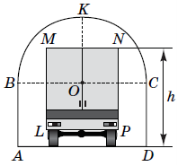
(2017)19. На рисунку зображено поперечний переріз аркового проїзду, верхня частина якого (дуга ) має форму півкола радіуса м. Відрізки і перпендикулярні до , м. Яке з наведених значень є найбільшим можливим значенням висоти вантажівки, за якого вона зможе проїхати через цей арковий проїзд, не торкаючись верхньої частини арки (дуги )? Уважайте, що – прямокутник, у якому м і .

А	Б	В	Г	Д
м	м	м	м	м

Відповідь: Г.

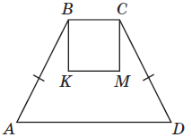
(2017)26. На рисунку зображено рівнобічну трапецію та квадрат . Точки і – середини діагоналей і трапеції відповідно. Площа квадрата дорівнює см².

1. Визначте довжину діагоналі (у см).

2. Обчисліть площу трапеції (у см²).

Відповідь: 1. ; 2. .

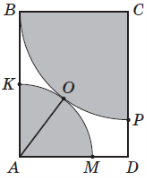
(2017)26. На рисунку зображено прямокутник і кругові сектори та , що мають одну спільну точку . Площа сектора дорівнює см², см.

1. Визначте радіус сектора (у см).

2. Обчисліть площу прямокутника (у см²).

Відповідь: 1. ; 2. .

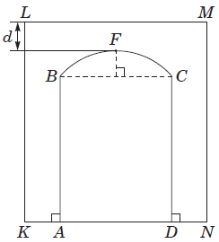
(2018)20. На рисунку зображено фрагмент поперечного перерізу стіни (прямокутник ) з арковим прорізом , верхня частина якого є дугою кола радіуса м. Відрізки і перпендикулярні до . м, , м. Визначте відстань від найвищої точки прорізу до стелі .

А	Б	В	Г	Д
м	м	м	м	м

Відповідь: Г.

(2018)24. Установіть відповідність між геометричною фігурою (1 – 4) та її площею (А – Д).

Геометрична фігура		Площа геометричної фігури
1	ромб зі стороною см і тупим кутом	А	см²
2	квадрат, у який уписане коло радіуса см	Б	см²
3	паралелограм, одна сторона якого дорівнює см, а висота, проведена з вершини тупого кута, ділить іншу сторону на відрізки завдовжки см і см	В	см²
4	прямокутник, більша сторона якого дорівнює см й утворює з діагоналлю кут	Г	см²
		Д	см²

Відповідь: 1 – Д; 2 – Б; 3 – В; 4 – Г.

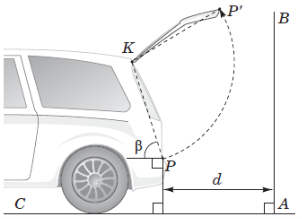
(2018)19. Автомобіль, задні дверцята якого відкриваються так, як зображено на рисунку, під’їжджає заднім ходом по горизонтальній поверхні перпендикулярно до вертикальної стіни . Укажіть серед наведених найменшу відстань від автомобіля до стіни , за якої задні дверцята автомобіля зможуть із зачиненого стану безперешкодно набувати зображеного на рисунку положення . м, . Наявністю заднього бампера автомобіля знехтуйте.

А	Б	В	Г	Д
м	м	м	м	м

Відповідь: Г.

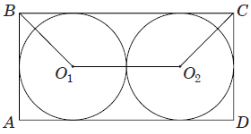
(2018)26. У прямокутник вписано два кола із центрами в точках та , кожне з яких дотикається до трьох сторін прямокутника й одне до одного (див. рисунок). Сума довжин уписаних кіл дорівнює .