Варіанти комплексної контрольної роботи з дисципліни "Вища математика"

Варіант 1

1. На першому курсі студенти мають 10 навчальних предметів і 5 різних занять на день. Скількома способами можна скласти відповідний розклад?
2. Розв’яжіть за формулами Крамера систему рівнянь:
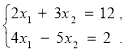
3. Дано два вектори: 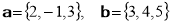 . Знайдіть вектор.

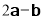Варіант 2

1. Знайдіть добуток комплексних чисел (1 – 2і)(3 + 2і).

2. Запишіть рівняння прямої, що проходить через точки М₁(1, 2, 3) і М₂(3, 5, 7).

3. Знайдіть суму площ двох сусідніх хвиль синусоїди

Варіант 3

1. Знайдіть суму двох матриць :
2. Знайдіть відстань d від точки М₁(1, 2, 3) до площини, заданої рівнянням .
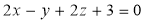3. Розв’яжіть нерівність:

Варіант 4

1. Скільки дев’ятицифрових чисел можна записати різ­ними значущими цифрами?
2. Обчислимо визначник:
3. Дано рівняння директрис гіперболи 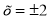, відстані між фокусами якої дорівнюють 10. Записати канонічне рівняння гіперболи.

Варіант 5

1. Знайдіть мінор М₁₁ визначника третього порядку:
2. Знайдіть

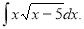
3. Дано просторовий трикутник з вершинами А(1, 2, –1), В(2, 4, 1), С(3, 0, 0). Знайдіть кут при вершині А.

Варіант 6

1. Із 10 кандидатів на одну й ту саму посаду мають бути обрані троє. Скільки існує варіантів вибору?
2. Обчислити площу фігури, обмеженої кривими 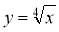і

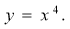
3. Обчислити відстань d від точки М₁(5, 3) до прямої 3х + 4у + 3 = 0.

Варіант 7

1. Знайдіть розв’язок системи рівнянь 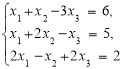за методом Гауса.
2.  Для деякого товару визначено виробничу функцію

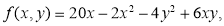
де x, y — фактори виробництва. Знайдіть граничну продуктивність фактора x.

3. Знайдіть канонічне рівняння еліпса, коли відомо, що .

Варіант 8

1. Знайдіть суму комплексних чисел  (– 3 + 5і) + (4 – 8і).
2. Знайдіть добуток матриць  ВА, якщо .
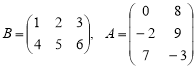3. Знайдіть координати фокуса параболи

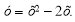
Варіант 9

1. Знайдіть
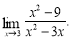
2. Для функції 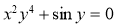Знайдіть .
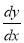3. Знайдіть ексцентриситет гіперболи  .

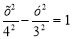Еталонна відповідь

Варіант 1

1. На першому курсі студенти мають 10 навчальних предметів і 5 різних занять на день. Скількома способами можна скласти відповідний розклад?

Розв’язання:

Усі можливі набори предметів становлять усі можливі розміщення з 10 елементів по 5. Отже, усіх таких способів існує

Відповідь: 30240 способів.

2. Розв’яжемо за формулами Крамера систему рівнянь:

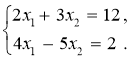
Розв’язання:

 Запишемо відповідні визначники і знайдемо розв’язки системи рівнянь:

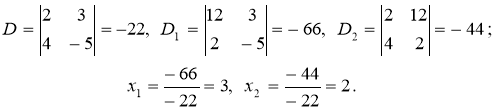
Відповідь: х₁=3, х₂=2.

3. Дано два вектори: 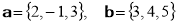. Знайдіть вектор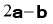

Розв’язання:

Знайдемо вектор  .

Відповідь: