Вектор (площинний випадок)
Вектор як напрямлений відрізок
(площинний випадок)
1) Розкриття поняття вектора, як напрямленого відрізка
Поняття вектора є одним із фундаментальних понять сучасної математики. Його можна визначати по-різному:
➢ як напрямлений відрізок;
➢ як упорядковану пару точок, що є кінцями напрямленого відрізка; ➢як паралельне перенесення.
Вектор характеризується числовим значенням (модулем) і напрямом.
Вектор зображають напрямленим відрізком, тобто відрізком зі стрілкою, яка показує напрям вектора.
Для позначення векторів використовують малі латинські букви: а, b, c...
або АВ… Перша з букв позначає початок, друга – кінець.
Риска або стрілка над назвою відрізка заміняє слово «вектор».
Щоб задати вектор, достатньо вказати його початок його кінець.
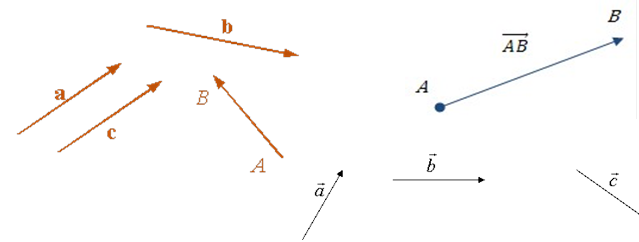
Рис. 1
2) Нульовий вектор
Вектор, у якого початок і кінець - одна й та сама точка, називають нульовим
![]()
вектором або нуль-вектором і позначають 𝟎 або 𝟎⃗

Про напрям нуль-вектора не говорять.
Довжина нуль-вектора дорівнює нулю: l⃗0 l=0. Нульовий вектор вважають колінеарним будь-якому вектору.
3) Колінеарні вектори
Ненульові вектори називають колінеарними, якщо вони лежать на паралельних прямих або на одній прямій.
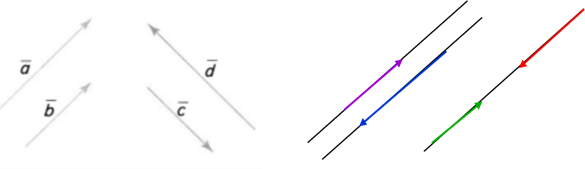
Рис. 3
Колінеарні вектори 𝑎 і 𝑏⃗ , які мають однаковий напрям, називають однаковонапрямленими (співнапрямленими), якщо промені АВ і СD однаково напрямлені, і записують:⃗а ⇈ 𝑏⃗ .
Колінеарні вектори⃗⃗⃗𝑎 і 𝑏⃗ , які мають протилежні напрями, називаютьпротилежнонапрямленими, якщопромені АВ і СD протилежно напрямлені,і записують:𝑎 ↑↓ 𝑏⃗ . Властивість та ознака колінеарних векторів:
у колінеарних векторів відповідні координати пропорційні і, навпаки:
якщо у двох векторів відповідні координати пропорційні, то ці вектори колінеарні.
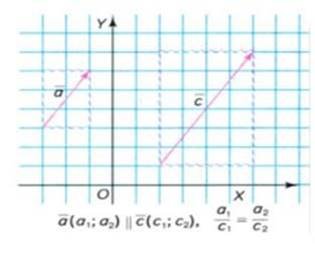
4) Співнапрямлені і протилежно напрямлені вектори
Якщо колінеарні вектори мають однаковий напрям, то їх називають співнапрямленими.
Якщо колінеарні вектори мають протилежний напрям, то їх називають протилежно напрямленими.
5) Рівні вектори
Вектори рівні тоді і тільки тоді, коли їх відповідні координати рівні. Рівні вектори співнапрямлені і рівні за абсолютною величиною. І навпаки, якщо вектори співнапрямлені і рівні за абсолютною величиною, то вони рівні.
Отже, вектори є рівними, якщо виконано дві умови:
1) вони однаково напрямлені;
2) їхні модулі рівні, тобто

6) Координати вектора
Нехай вектор ⃗а має початком точку А1(х1;𝑦1), а кінцем – точка А2(х2;𝑦2).
Координатами вектора ⃗а називаються числа 𝑎1= х2- х1, 𝑎2= 𝑦2- 𝑦1
Коротко записують:
➢ 𝑎̅(𝑎1; 𝑎2) і читають: вектор а з координатами𝑎1 і 𝑎2; ➢ ̅АВ̅̅̅ (𝑎1; 𝑎2) і читають: вектор̅ АВ̅̅̅̅ з координатами 𝑎1 і 𝑎2;
➢ ![]() (𝑎1; 𝑎2) і читають: вектор з координатами𝑎1 і 𝑎2.
(𝑎1; 𝑎2) і читають: вектор з координатами𝑎1 і 𝑎2.
Координати нуль-вектора дорівнюють нулю: 0̅ (0; 0).
Протилежні вектори мають протилежні відповідні координати.
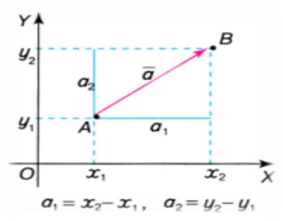
Рис. 4
Важливо: поняття координат вектора відрізняється від поняття координат точки на площині. Наприклад, точку М (2;1) можна позначити на координатній площині і ця точка буде єдиною. Знаючи координати точки, завжди можна знайти її положення на площині (у даному випадку І чверть). А ось векторів з координатими (2; 1) на площині можна зобразити безліч, головне, щоб різниці координат кінця і початку векторів були однакові, а вказати конкретно чверть, де знаходиться вектор з координатими (2; 1), – неможливо.
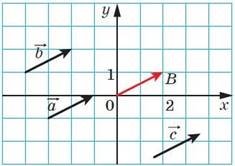
Рис. 5
7) Абсолютна величина вектора
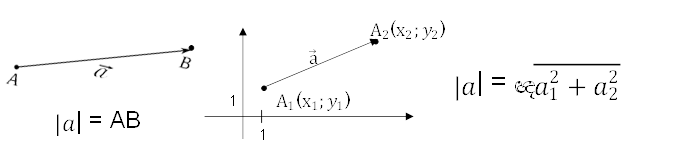 Абсолютною величиною (або модулем) вектора називається довжина відрізка, що задає вектор.
Абсолютною величиною (або модулем) вектора називається довжина відрізка, що задає вектор.
Вектор, який має довжину рівну одиниці, називається одиничним вектором. Тобто, якщо |⃗е |=1, то ⃗е −одиничний вектор
8) Сума векторів
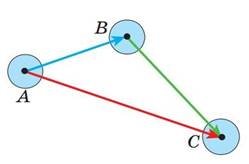
Якщо тіло перемістилося з точки A в точку B, а потім із точки B у точку C, то сумарне переміщення з точки A в точку C природно подати у вигляді
![]()
![]() вектора АС, вважаючи цей вектор сумою векторів AB і BC, тобто AB + BC = AC.
вектора АС, вважаючи цей вектор сумою векторів AB і BC, тобто AB + BC = AC.
![]() Рис. 6 Правила додавання двох векторів: правило трикутника: відкладемо від довільної точки A вектор AB, рівний
Рис. 6 Правила додавання двох векторів: правило трикутника: відкладемо від довільної точки A вектор AB, рівний
![]()
![]() вектору
вектору 𝑎. Далі від точки B відкладемо вектор BC, рівний вектору b. Вектор AC називають сумою векторів a і b і записують: a + b = AC.
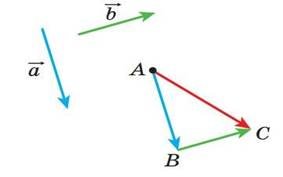
Рис. 7
За правилом трикутника можна додавати й колінеарні вектори.
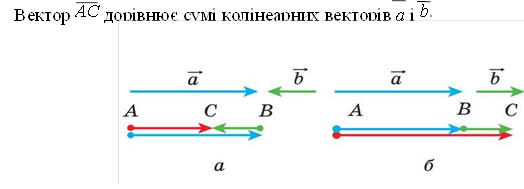
Рис. 8
![]()
Для будь-яких трьох точок A, B і C виконується рівність AB+ BC = AC, яка виражає правило трикутника для додавання векторів; правило паралелограма (для знаходження суми двох неколінеарних векторів, відкладених від однієї точки):
![]()
![]()
відкладемо від довільної точки A вектор AB, рівний вектору 𝑎, і вектор AD,
![]()
![]() рівний вектору b. Побудуємо паралелограм ABCD. Тоді шукана сума 𝑎 + b дорівнює вектору A
рівний вектору b. Побудуємо паралелограм ABCD. Тоді шукана сума 𝑎 + b дорівнює вектору A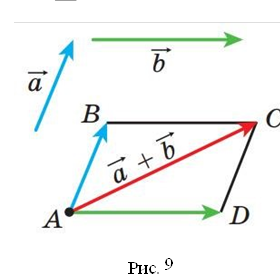 C.
C.
Правила додавання кількох векторів: сума кількох векторів визначається за допомогою правила многокутника, яке є узагальненням правила трикутника. Якщо вектори відкладені так, що початок другого вектора збігається з кінцем першого, початок третього – із кінцем другого і т.д., то сума дорівнює вектору, початок якого збігається з початком першого, а кінець – із кінцем останнього вектора, тобто 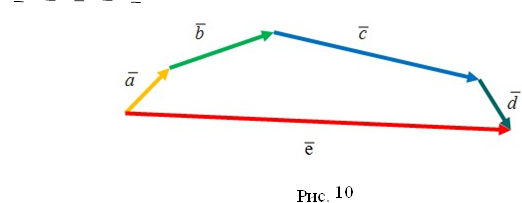 𝑎 + b + c + d = e
𝑎 + b + c + d = e
Властивості додавання векторів:
![]() для будь-яких векторів 𝑎, b і c виконуються рівності:
для будь-яких векторів 𝑎, b і c виконуються рівності:
1) a +0 = a – додавання нуль-вектора;
2) ![]()
a + b = b + a – переставна властивість;
![]() 3)(a+b)+c=
3)(a+b)+c= a +(b + c)– сполучна властивість; 4) a + ( - a ) = 0– додавання протилежних векторів.
9) Різниця векторів Означення різниці векторів:
![]()
![]()
![]() різницею векторів a і b називають такий вектор c , сума якого з вектором b дорівнює вектору
різницею векторів a і b називають такий вектор c , сума якого з вектором b дорівнює вектору a.
![]() Пишуть:
Пишуть: c= a - b.
Побудова вектора, який є різницею двох векторів:
![]() a
a 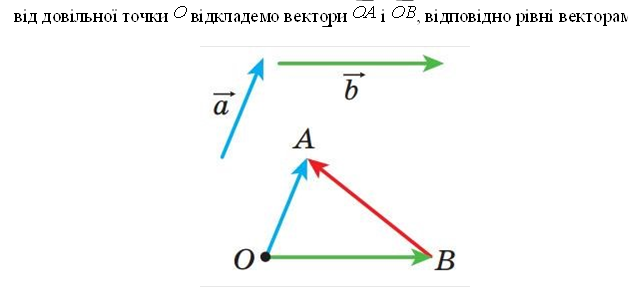 і b. Тоді вектор BA дорівнює різниці a - b.
і b. Тоді вектор BA дорівнює різниці a - b.
Рис. 11
Описаний алгоритм можна застосовувати й для знаходження різниці колінеарних векторів.
![]()
![]() Вектор BA дорівнює різниці колінеарних векторів
Вектор BA дорівнює різниці колінеарних векторів a і b.

Рис. 12
10) Множення вектора на число Означення множення вектора на число:
![]() добутком ненульового вектора 𝑎 і числа k, причому k≠0, називають
добутком ненульового вектора 𝑎 і числа k, причому k≠0, називають
![]() такий вектор b, що:
такий вектор b, що:
1) |b| = |k| | 𝑎|;
2) ![]()
![]() якщо k > 0, то b ↑↑𝑎; якщо k < 0, то b↑↓𝑎. Пишуть: b = k 𝑎.
якщо k > 0, то b ↑↑𝑎; якщо k < 0, то b↑↓𝑎. Пишуть: b = k 𝑎.
![]() Якщо
Якщо 𝑎=0 або k = 0, то вважають, що 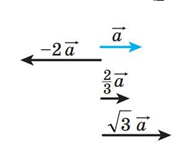 k 𝑎=0.
k 𝑎=0.
Рис. 13
Властивості множення вектора на число:
![]() для будь-яких чисел k, m і будь-яких векторів 𝑎, b виконуються рівності:
для будь-яких чисел k, m і будь-яких векторів 𝑎, b виконуються рівності:
1) 1 𝑎 = 𝑎;
2) ![]() - 1 𝑎 = 𝑎;
- 1 𝑎 = 𝑎;
3) k 0 = 0 𝑎 = 0;
4) k 𝑎 = 𝑎k
5) ![]() (km)𝑎 = k (m𝑎) - сполучна властивість;
(km)𝑎 = k (m𝑎) - сполучна властивість;
6) (k + m)𝑎 = k 𝑎 + m 𝑎 — перша розподільна властивість;
7) k (𝑎 + b) = k 𝑎 + kb — друга розподільна властивість.
![]() Абсолютна величина вектора ka:
Абсолютна величина вектора ka: ![]() |k
|ka| = |k| | 𝑎| Умова колінеарності двох ненульових векторів a і b:
![]()
![]() якщо вектори 𝑎 і b -колінеарні й
якщо вектори 𝑎 і b -колінеарні й ![]() ≠0, то існує таке число k, що b = k
≠0, то існує таке число k, що b = k 𝑎.
Дії над векторами у координатному поданні
Позначення вектора, заданого своїми координатами: якщо вектор𝑎 має координати 𝑎1 і 𝑎2, то його позначають:
![]() 𝑎(𝑎1 ;𝑎2) або (𝑎1 ;𝑎2).
𝑎(𝑎1 ;𝑎2) або (𝑎1 ;𝑎2).
Сума двох векторів:
![]()
![]()
![]() сумою векторів 𝑎 і b з координатами (𝑎1 ;𝑎2) і (𝑏1 ;𝑏2) називається вектор с з координатами (𝑎1 + 𝑏1; 𝑎2 + 𝑏2), тобто
сумою векторів 𝑎 і b з координатами (𝑎1 ;𝑎2) і (𝑏1 ;𝑏2) називається вектор с з координатами (𝑎1 + 𝑏1; 𝑎2 + 𝑏2), тобто
𝑎(𝑎1 ;𝑎2) + b(𝑏1 ;𝑏2) = c(𝑎1 + 𝑏1; 𝑎2 + 𝑏2). Різниця двох векторів:
![]()
![]() різницею векторів 𝑎(𝑎1 ;𝑎2) і b(𝑏1 ;𝑏2)називається такий вектор с(с1; с2) який у сумі з вектором b дає вектор 𝑎: b +
різницею векторів 𝑎(𝑎1 ;𝑎2) і b(𝑏1 ;𝑏2)називається такий вектор с(с1; с2) який у сумі з вектором b дає вектор 𝑎: b + c = 𝑎. Добуток вектора 𝒂(𝒂𝟏 ;𝒂𝟐) на число k:
![]()
![]() добутком вектора (𝑎1 ;𝑎2) на число k називається вектор (k𝑎1 ;𝑘𝑎2),
добутком вектора (𝑎1 ;𝑎2) на число k називається вектор (k𝑎1 ;𝑘𝑎2),
![]() тобто(𝑎1 ;𝑎2)k=(k 𝑎1 ;𝑘𝑎2). Ознака колінеарності двох векторів : у колінеарних векторів відповідні координати пропорційні і, навпаки: якщо у двох векторів відповідні координати пропорційні, то ці вектори колінеарні,
тобто(𝑎1 ;𝑎2)k=(k 𝑎1 ;𝑘𝑎2). Ознака колінеарності двох векторів : у колінеарних векторів відповідні координати пропорційні і, навпаки: якщо у двох векторів відповідні координати пропорційні, то ці вектори колінеарні,
𝑎1 𝑎2 𝑎1 𝑏1
тобто = або = 𝑏1 𝑏2 𝑎2 𝑏2
11) Скалярний добуток векторів
Скалярним добутком двох векторів ⃗𝒂⃗ і ⃗𝒃⃗ буде скалярна величина (число), що дорівнює добутку модулів цих векторів, помножене на косинус кута між ними: ⃗𝒂⃗ ![]()
![]() =
=![]() cosα
cosα
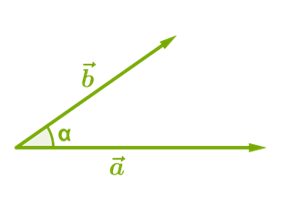
Рис. 14
̂ ⃗𝒃⃗ =α.
Кут між векторами позначають ⃗𝒂⃗
Скалярний добуток векторів:
![]()
➢скалярний добуток векторів a(𝑎1 ;𝑎2) і b(𝑏1 ;𝑏2) дорівнює сумі добутків відповідних координат цих векторів:
![]()
ab = 𝑎1𝑏1+ 𝑎2𝑏2;
➢скалярним добутком двох ненульових векторів називають число, що
![]() дорівнює добутку їх довжин та косинуса кута між ними:
дорівнює добутку їх довжин та косинуса кута між ними: ab = ![]() )
)
𝑎⃗ 𝑏⃗
𝑐𝑜𝑠 ![]() =
=![]()
![]()
Властивості скалярного множення векторів:
![]() для будь-яких векторів
для будь-яких векторів a, b, c і будь-якого числа k виконуються рівності:
1) ab=ba- переставна властивість;
![]() 2)(k
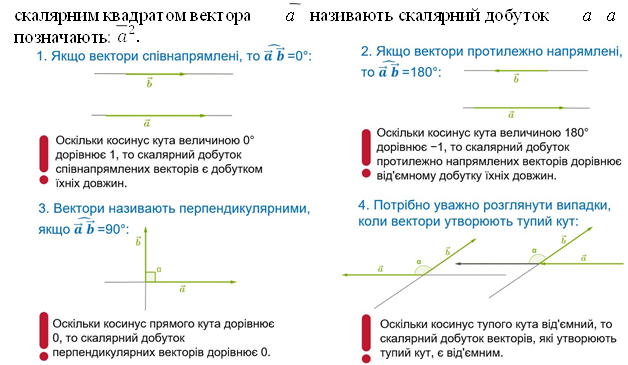
2)(ka)b=k(ab) - сполучна властивість (відносно скалярного множника); 3) (a+b )c = ac + bc - розподільна властивість. Скалярний квадрат вектора а:
12) Приклади задач
№1. Дано три точки А(2;2), B(-2;0), C(0;2). Знайдіть таку точку D(x;y), щоб вектори ⃗𝐴𝐷⃗⃗⃗⃗ і ⃗С⃗⃗⃗𝐷⃗ були рівні.
Розв'язання
𝐴⃗⃗⃗⃗В⃗ (−4;2), ⃗𝐶𝐷⃗⃗⃗⃗ (𝑥−0;𝑦−2)
Оскільки ⃗𝐴𝐷⃗⃗⃗⃗ = ⃗С⃗⃗⃗𝐷⃗ за умовою, то: x-0=4; y-2=-2
Звідси знаходимо координати точки D: x=-4; y=0
Відповідь: D (-4;0)
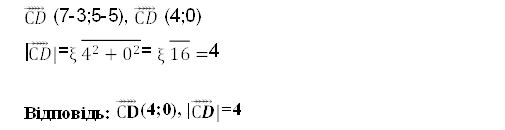
№2. Знайти координати і абсолютну величину вектора ⃗С⃗⃗⃗𝐷⃗ , якщо
С (3;5), D (7;5)
Розв'язання
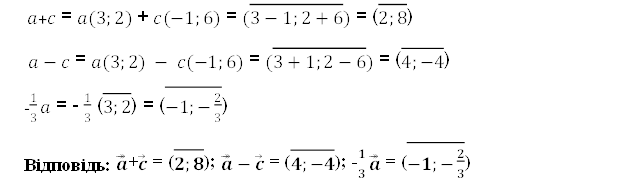
№ 3. Дано вектор 𝑎 (3;2) і 𝑐 (−1;6) були рівні. Знайдіть координати векторів: 𝑎 +𝑐 , 𝑎 −𝑐 , -![]() 𝑎
𝑎
![]()
Розв'язання
№4. Доведіть, що вектори 𝑎 і с перпендикулярні, якщо 𝑎 (3;2), 𝑐 (6;−9)
Розв'язання
Якщо вектори перпендикулярні, то їхній скалярний добуток дорівнює нулю:
𝑎 ![]() =0,
=0, ![]() = 3
= 3![]() 6-2
6-2![]() 9 = 0, тобто 𝑎
9 = 0, тобто 𝑎 ![]() с . Що і треба було довести.
с . Що і треба було довести.
№5. Знайдіть кут між векторами 𝑎 і 𝑏⃗ , якщо |𝑎 | ![]()
Розв'язання
𝑎 ![]()
![]() =
=![]() cosα;
cosα;
𝑐𝑜𝑠![]() = 𝑎⃗ 𝑏⃗ ;
= 𝑎⃗ 𝑏⃗ ;
![]()
𝑐𝑜𝑠![]() ;
;
![]() =
=![]()
Відповідь: α=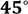


про публікацію авторської розробки
Додати розробку
