Відкрите заняття на тему "Розв’язування вправ на паралельність площин"

Передмова

 

 На сучасному рівні розвитку цивілізації особливу роль відіграє інноваційний потенціал суспільства, що потребує спеціалістів, здатних системно й конструктивно мислити, швидко знаходити потрібну інформацію, приймати адекватні рішення, створювати принципово нові ідеї в різних галузях знань. А це, в свою чергу, формує соціальне замовлення на нові підходи в системі освіти, нове педагогічне мислення, нове ставлення педагога до своєї діяльності, результатом якої має бути виховання «інноваційної людини».

 Представлена методична розробка з теми «Розв’язування вправ на паралельність площин» дає можливість познайомитись з застосуванням технології модульного навчання.  Модульне навчання характеризується випереджаючим вивченням теоретичного матеріалу укрупненими блоками - модулями, алгоритмізацією навчальної діяльності, завершеністю і узгодженістю циклів пізнання та інших циклів діяльності. Рівнева індивідуалізація і диференціація навчальної діяльності створюють ситуацію вибору для викладача і студента. Модульне навчання уможливлює: формування навичок самоосвіти учнів, що вкрай важливо в сучасних умовах; формування вміння усвідомленого цілепокладання; формування навичок співпраці, взаємоконтролю і самоконтролю.

Проведення заняття ведеться у відповідності до технологічної карти заняття, супроводжується слайдами презентації, мотивується різними фактами застосування паралельності площин в промисловості та побуті.

Представлена методична розробка практичного заняття демонструє один з варіантів вивчення обраної теми, допомагає спонукати студентів до самостійного мислення і ухвалення рішень.

 

 

 

 

 

ПЛАН    ЗАНЯТТЯ 

 

Дисципліна : Математика

Дата : 06.03.19            

Група : ЕТ-18

Кількість студентів за списком: 23

Спеціальність: 141 «Електроенергетика, електротехніка та електромеханіка»

Місце проведення: кабінет вищої математики,  № 28

 

Тема заняття : Розв’язування вправ на паралельність площин             

 

Мета заняття:

 

Методична – впроваджувати в освітній процес особистісно орієнтований підхід 

                        шляхом технології модульного навчання;

Дидактична – працювати над подальшим засвоєнням студентами означення, ознаки та властивостей паралельності площин, формувати уміння та навички використовувати вивчені твердження при розв’язанні вправ, творчого підходу до вирішення завдань на побудову перетинів;

Розвиваюча – розвивати у студентів навички дослідницької роботи, пам’ять, уміння проводити самоконтроль і взаємоконтроль;

Виховна  –       виховувати здатність до розв’язання проблемних ситуацій,

                        почуття відповідальності, організованості, наполегливість у

                        досягненні мети, формувати вміння працювати в команді.

 

Вид заняття : практичне заняття

 

Тип заняття : застосування знань, умінь та навичок

 

Форми і методи роботи на занятті: фронтальний опрос, робота в міні-групах, докладне коментування кроків рішення вправи, фронтальна бесіда, тестування, демонстраційний, дослідницький, систематизації

 

Методичне забезпечення:

•          Технологічна карта заняття;
•          Таблиці  «Аксіоми стереометрії», «Паралельність у просторі»;
•          Картки контролю теоретичних знань;
•        Презентація заняття.

 

Технічні засоби навчання:

•           Мультимедійний проектор
•           Персональний комп’ютер

 

Міжпредметні зв’язки:

Забезпечуючі:  «Українська мова», «Технології: Креслення», «Інформатика»

Забезпечуємі: «Інженерна та комп’ютерна графіка», «Теоретичні основи електротехніки», «Електропостачання підприємств і цивільних споруд»

 

Література

Основна:

1. Бевз Г. П.Математика : Алгебра і початки аналізу та геометрія.  Рівень стандарту : підруч. для 10 кл. закладів загальної середньої освіти / Г. П. Бевз, В. Г. Бевз. — К. : Видавничий дім «Освіта», 2018.

 

2. Афанасьєва О.М., Бродський Я.С., Павлов О.Л., Сліпенько А.К. Математика. Підручник. К., Вища школа, 2001

 

3.  Нелін Є.П. Алгебра та початки аналізу: підручник для 10 класу загальн.учбових закладів. Х.: Гімназія, 2010

 

Додаткова :

1. Богомолов II.В. Практические занятия по математике.  М.: Высш. шк., 1979, 1983, 1990

2. Афанасьєва О.М., Бродський Я.С., Павлов О.Л., Сліпенко А.К. Дидактичні матеріали з математики. К., Вища школа, 2001

 

3. Збірник заданий для державної підсумкової атестації з математики. 11 класс. Ред. З.І. Слєпкань. – Харьків, “Гімназія”, 2014

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Хід і зміст заняття

 

      1. Організаційний момент.                                                                        1 хв.   

Привітання зі студентами

Відмітка у журналі відсутніх

Перевірка готовності до заняття студентів, аудиторії

 

2. Ознайомлення студентів з темою та навчальними цілями заняття    2 хв.

 

•          Тема:  Розв’язування вправ на паралельність площин             

На цьому занятті ми систематизуємо теоретичний матеріал про паралельні площини, перевіримо рівень засвоєння теоретичного матеріалу та будемо формувати уміння застосовувати цей матеріал до розв’язання вправ.

 

3. Актуалізація опорних знань. Мотивація  навчання.                       15 хв.

Мета. Повторити основні теоретичні знання з теми «Паралельність площин»

Викладач. Дві площини паралельні, якщо дві пересічні прямі, що лежать в одній площині, відповідно паралельні двом прямим, що лежать в іншій площині.

Як часто ми стикаємося з ознакою паралельності в нашому житті, на практиці? Всі живуть в будинках, де підлога і стеля паралельні, інакше будівлі не встоять у вертикальному положенні. Це закони архітектури, де широко застосовують ознаку паралельності площин. Спускаючись по сходах, ми тримаємося за перила, які теж паралельні. На вулиці ми бачимо телеграфні стовпи з електричними дротами, які теж паралельні, інакше відбудеться коротке замикання. Сідаючи в тролейбус, ми бачимо його "роги", які з'єднані з електричними паралельними проводами, а в метро, ми піднімаємося по ескалатору, що має паралельні поручні і сходинки. На виробництвах можна побачити безліч транспортерів для переміщення виробів - це теж використання ознаки паралельності, інакше лінія транспортера не зможе рухатися. Ну і звичайно, залізничні рейки, якщо вони не паралельні, то потяги по них не поїдуть. Тому, ознака паралельності площин широко і повсюдно використовується на практиці і в нашому житті.

Крім того, при виконанні курсових і дипломних проектів для побудови креслень необхідно буде спиратись на знання сьогоднішньої теми.

1. Повторення основних тверджень про паралельність площин

Викладач. Як можуть розташовуватись дві площини?

(Дві площини у просторі можуть перетинатися, або бути паралельними)

Викладач. Які площини називають паралельними?

(Дві площини що не перетинаються називають паралельними)

Викладач. Коли дві площини паралельні?

(Якщо дві прямі, які перетинаються, однієї площини відповідно паралельні двом прямим іншої  площини, то ці площини паралельні)

Викладач. Як називаємо ми це твердження? (Це ознака паралельності площин)

Викладач. Якщо дві паралельні площини перетнути третьою площиною, то що ми отримаємо?

(Паралельні площини перетинаються  січною площиною по паралельним прямим)

Викладач. Як називаємо ми це твердження? (Це перша властивість паралельних площин)

Викладач. Сформулюйте другу властивість паралельності площин (Відрізки паралельних прямих, розташованих між паралельними площинами, рівні)

2.               Перевірка знань теоретичного матеріалу

Робота в міні-групах: формулювання твердження кожним студентом.

Студенти розповідають 4 твердження в групі, а потім викладач або консультант приймає знання теорії у цій групі.

 

4. Застосування знань в стандартних умовах                                       25 хв.

Вправа № 981.

Відрізки OA, OB, OC не лежать в одній площині. Доведіть, що площина, яка проходить через їх середини, паралельна площині (ABC) (мал. 244).

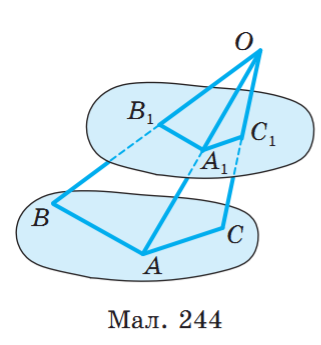Дано: ОА, ОВ, ОС - відрізки

В₁ОВ, ОВ₁ = ВВ₁,

А₁ОА, ОА₁ = АА₁,

С₁ОС, ОС₁ = СС₁

Довести: (А₁В₁С₁) || (АВС)

Доведення

1. (А₁В₁С₁) = α (акс. С₃)
2. В АВС А₁В₁  - середня лінія

АВ ||А₁В₁

Аналогічно, АС ||А₁С₁

3. АВ∩АС = А, А₁В₁ ∩А₁С₁ = А₁,

І ці прямі попарно паралельні 

(АВС) || α (за ознакою паралельності площин), що і т.д.

Завдання. Наступну задачу виконуємо по міні-групах:

група 1 – а), група 2 – б), група 3 – в)

Вправа № 994. Через точку C, яка лежить поза паралельними площинами α і β, проведено прямі a і b, що перетинають площину α в точках A і A₁, а площину β — у точках B і B₁ відповідно. Знайдіть AA₁, якщо:

а)  AC = 2 см, AB = 6 см, BB1 = 10 см;

б)  AC : BC = 1 : 3, BB₁ = 9 см;

в)  A1C : A₁B₁ = 2 : 3, BB₁ = 10 см;

г)  AC = 2 м, BB₁ = 8 м, CB = AA₁.

Викладач. З чого ви почнете виконання цієї вправи?

• З малюнка,
• На що треба звернути увагу? прямі АА₁ || ВВ₁

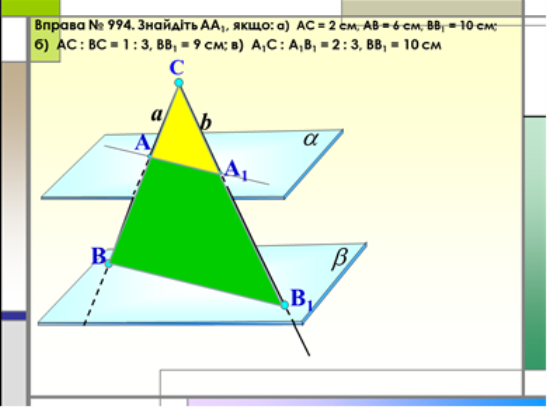
Розв’язок.

1) так як А  α,  А₁  α, то АА₁  α  (акс.С₂), аналогічно, ВВ₁  α;

2) так як α || β, а ∩ b = C, то АА₁ ||  ВВ₁ (за властивістю паралельних площин)

3) ВВ₁С ~АА₁С (за двома кутами, С – спільний, А = В, як відповідні) 

, тоді:

а) АС = 2 см, АВ = 6 см  ВС = АС + АВ = 8 (см)   АА₁ = 2,5 (см)

б) АС: ВС = 1 : 3, тоді  АА₁ = 3 (см)

в) А₁С : А₁В₁ = 2 : 3  А₁С : В₁ С= 2 : 5   АА₁ = 4 (см)

Відповідь: 2,5 см, 3 см, 4 см.

 

5. Застосування знань в нових умовах                                                          15 хв.

Мета. Навчити застосовувати теоретичний матеріал при виконанні перерізів многогранників.

Фронтальна бесіда викладача зі студентами по готовим слайдам

Викладач. Як можна задати площину у просторі?

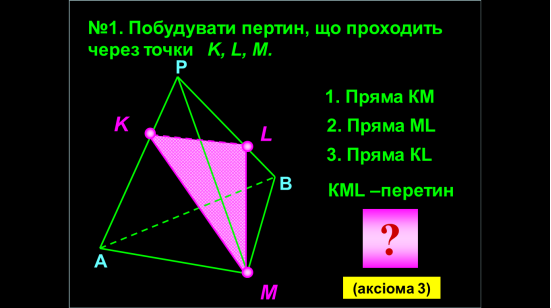
• За трьома точками (аксиома 3)
• За прямою та точкою, що їй не належить (наслідок 1)
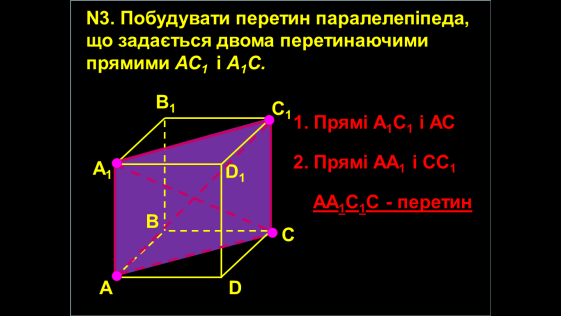
• За двома перетинаючими прямими (наслідок 2)
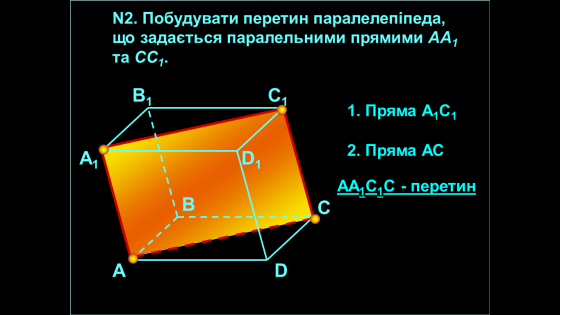
• За двома паралельними прямими (за визначенням паралельних прямих)

Викладач. Яке може бути розташування багатогранника і площини у просторі?

 

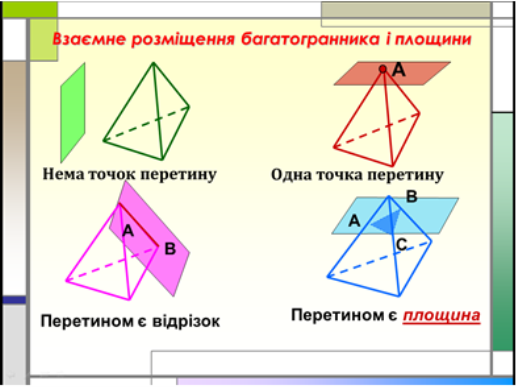
Викладач. Запишемо в зошит означення:

Багатокутник, отриманий при перетині багатогранника і площини, називається перетином багатогранника зазначеною площиною

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

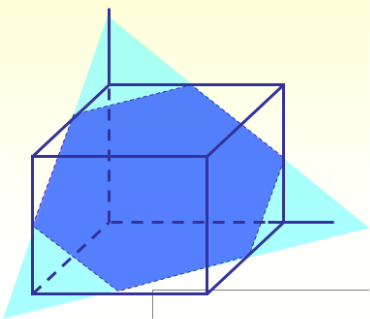
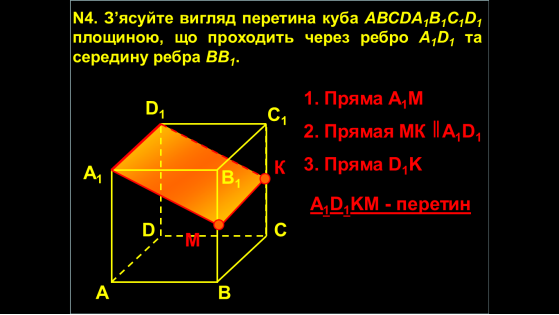
Ми з вами вже будували перетини багатогранників. Давайте пригадаємо, як це ми з вами робили?

 

 

 

 

 

 

 

 

 

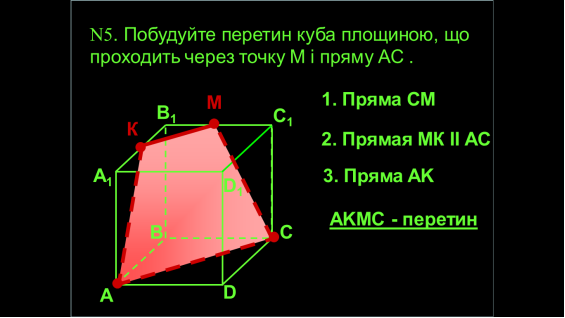
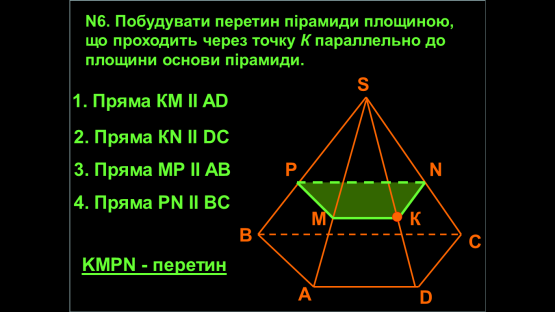
6. Виконання самостійної роботи                                                              15 хв

Мета. Перевірити уміння самостійно застосовувати отримані знання.

Оцінювання. За кожну правильну відповідь тестування 1 бал, за кожну правильну побудову  – 2 бали. Всього 10 балів.

Завдання. Кожен студент в аркуші самостійної роботи в частині тестування вибирає одну правильну (на його думку) відповідь, а в другій частині виконує побудову перетину багатокутника на готових малюнках та записує свої дії. (Додаток А)

Запишіть, будь ласка, у зошит правильні відповіді на тестові завдання для самоперевірки:

варіант	1	2	3	4	5	6
1 варіант	А	Б	А	Б	В	Б
2 варіант	Б	В	Б	А	Г	Б

Відповіді завдань на побудову

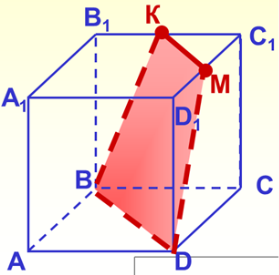
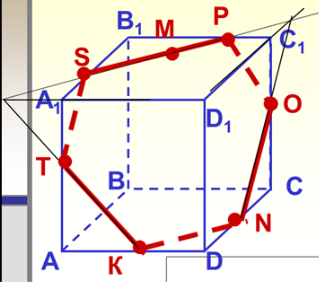Варіант 1.      № 7                                                              № 8

 

 

 

 

 

 

 

 

 

 

Варіант 2.

 

 

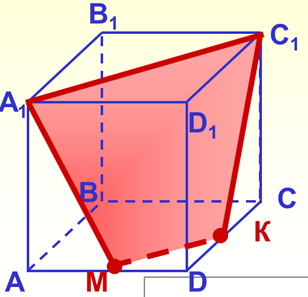
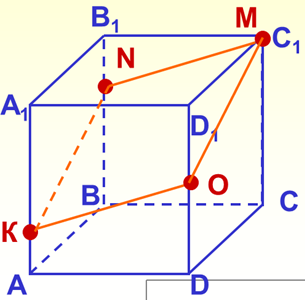
Перевірка виконується по готових малюнках

7. Повідомлення домашнього завдання                                                   3 хв.

[1], Р. 4,§ 27, с.200, виконати № 994 (г), 997, с.204-205, повторити  ОК

№ 994. Через точку C, яка лежить поза паралельними площинами α і β, проведено прямі a і b, що перетинають площину α в точках A і A₁, а площину β — у точках B і B₁ відповідно. Знайдіть AA₁, якщо:г) A C = 2 м, BB1 = 8 м, CB = AA₁.
№ 997. Точка A1 ділить ребро PA правильного тетраедра PABC у відношенні

PA₁ : A₁A = 2 : 3. Побудуйте переріз тетраедра площиною, яка паралельна площині (ABC) і проходить через точку A₁. Знайдіть площу перерізу, якщо

AB = 20 см

 

8. Підведення підсумків заняття.                                                               2 хв.

Підводяться результати теоретичного блоку знань та називаються студенти, які заробили на занятті додаткові оцінки та бали

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Викладач _________________ Козлова Г.В.

Додаток А

Картки контролю теоретичних знань та побудови

Варіант 1.

 

1. Якщо дві суміжні сторони паралелограма паралельні площині α, то площина паралелограма і площина α:

А) паралельні; Б) перетинаються; В) збігаються або паралельні; Г) паралельні або перетинаються.

2. Якщо діагоналі трапеції паралельні площині α, то основи трапеції:

А) лежать у площині α; Б) паралельні площині α; В) перетинають площину α; ; Г) можуть перетинати площину α, а можуть бути паралельними цій площині.

3. Основа AD трапеції АВСD лежить у площині α. Через точку М – середину АВ, проведено площину β , паралельну площині α, що перетинає СD в точці N. Прямі МN і ВС:

А) паралельні; Б) мимобіжні; В) перетинаються; Г) збігаються.

4. Скільки площин, паралельних заданій площині, можна провести через подану точку простору?

А) жодної; Б) одну; В) безліч; Г) відповідь залежить від розміщення поданої точки відносно заданої площини.

5. Якщо лінії перетину площин α і β  площиною γ паралельні, то площини α і β:

А) паралельні; Б) перетинаються; В) можуть бути паралельними або перетинатися; Г) паралельні чи збігаються.

6. У кубі АВСDА₁В₁С₁D₁ проведено два перерізи: через точки А, В₁, С і через точки А, D, С₁. Площини цих перерізів:

А) збігаються; Б) перетинаються; В) паралельні; Г) можуть бути розміщені по-різному, і це залежить від розмірів куба.

7. Побудуйте перетин куба площиною, що проходить через діагональ основи ВD і точку К, що належить стороні В₁С₁.

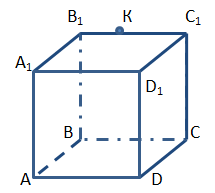
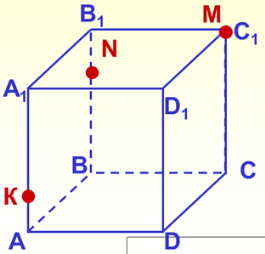
8. Побудуйте перетин куба, що проходить через точки К, M, N, якщо К  АD,  N  DС, точка М – на грані А₁В₁С₁D₁.

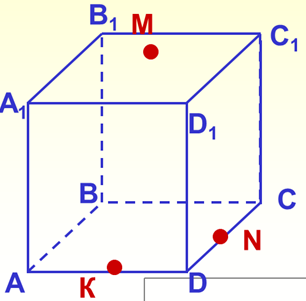
ІІ варіант

1. Якщо дві суміжні сторони трапеції паралельні площині α, то площина трапеції і площина α:

А) перетинаються; Б) паралельні; В) збігаються чи паралельні; Г) паралельні чи перетинаються.

2. Дві сторони трикутника паралельні деякій площині α. Отже третя сторона трикутника ...

А) лежить у площині α; Б) перетинає площину α; В) паралельна площині α; Г) може перетинати площину α.

3. Сторона АС трикутника АВС лежить у площині α. Через точку М – середину сторони АВ, проведено площину β , паралельну площині α, що перетинає ВС в точці К. Прямі МК і АС:

А) перетинаються; Б) паралельні; В) мимобіжні; Г) збігаються.

4. Скільки існує паралельних заданій прямій площин, що проходять через подану точку простору?

А) безліч; Б) одну; В) жодної; Г) відповідь залежить від взаємного розміщення точки і прямої.

5. Якщо дві площини паралельні одній і тій самій прямій, то ці площини:

А) паралельні; Б) перетинаються; В) збігаються; Г) паралельні чи перетинаються.

6. У кубі АВСDА₁В₁С₁D₁ проведено два перерізи: через точки А₁, В, С₁ і через точки А₁, D₁, С. Площини цих перерізів:

А) збігаються; Б) перетинаються; В) паралельні; Г) можуть розміщуватися по-різному, це залежить від розмірів куба.

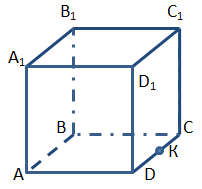
7. Побудуйте перетин куба площиною, що проходить через діагональ основи A₁C₁ і точку К, що належить стороні DС.

8. Побудуйте перетин куба, що проходить через точки К, M, N, якщо К  АА₁,  N  ВВ₁, точка М збігається з вершиною С₁.