Презентація до заняття "Розв'язання вправ на паралельність площин"
Про матеріал
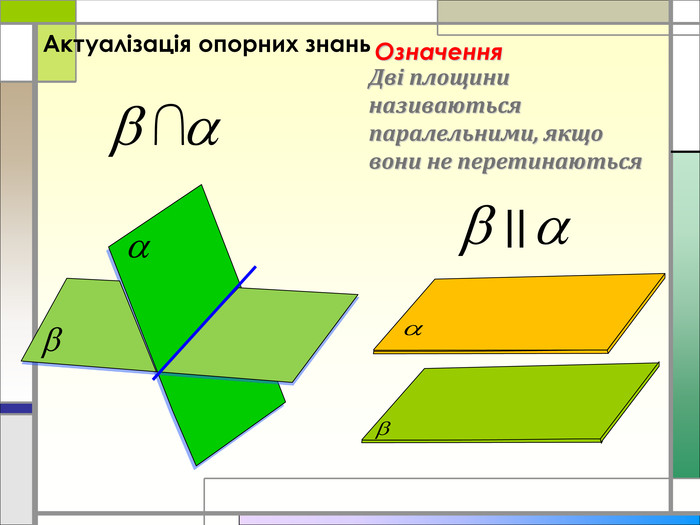
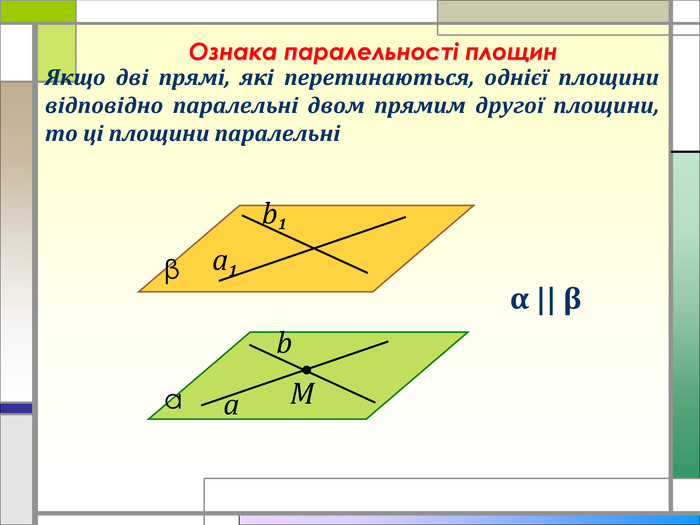
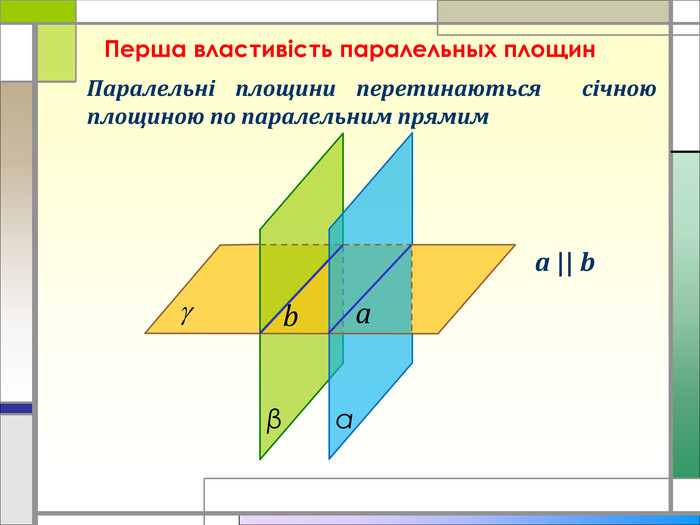
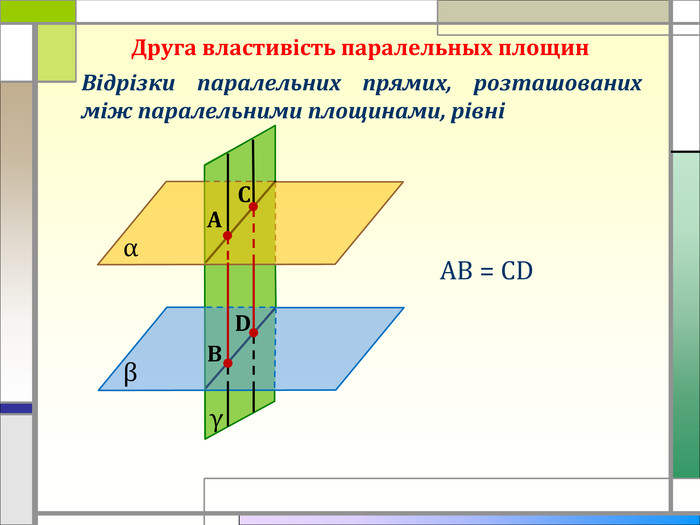
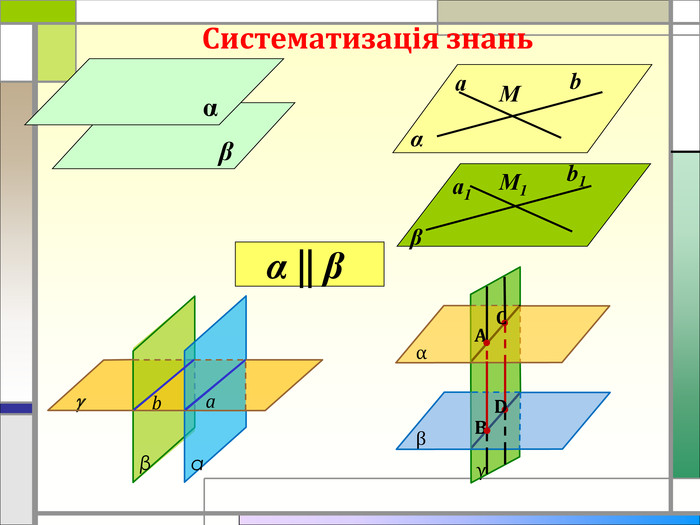
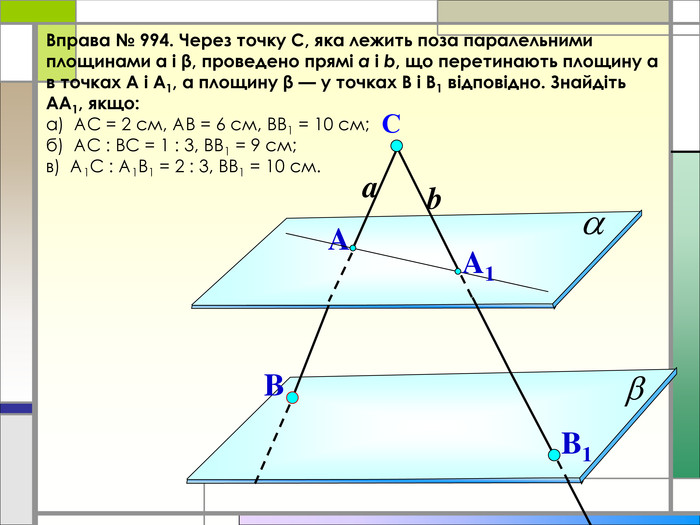
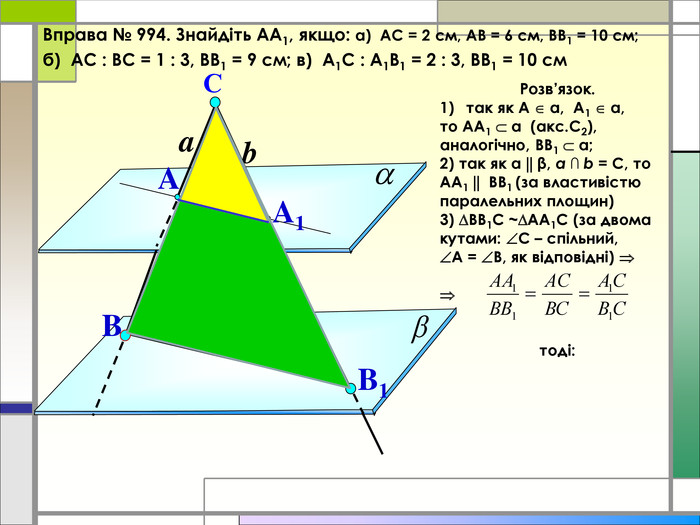
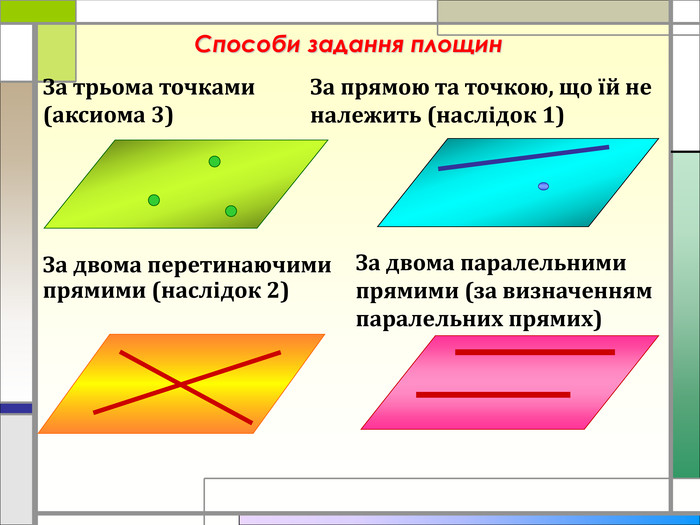
Дана презентація є супроводом проведення практичного заняття з теми "Розв'язання вправ на паралельність площин", дає можливість наочно побачити застосування цієї теми в повсякденному житті Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку












![Повідомлення домашнього завдання [1], Р. 4,§ 27, с.200, виконати № 994 (г), 997, с.204-205, повторити ОКА1 С1 В1 АР СВ Повідомлення домашнього завдання [1], Р. 4,§ 27, с.200, виконати № 994 (г), 997, с.204-205, повторити ОКА1 С1 В1 АР СВ](/uploads/files/494565/120626/132124_images/28.jpg)








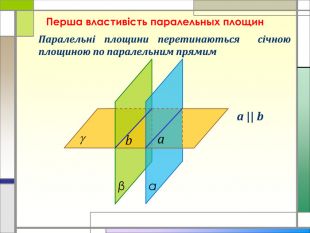
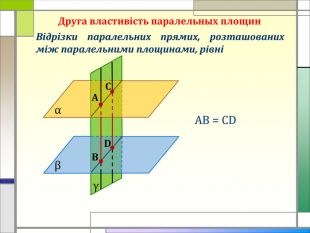
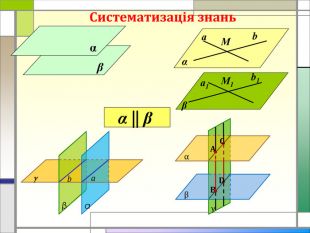
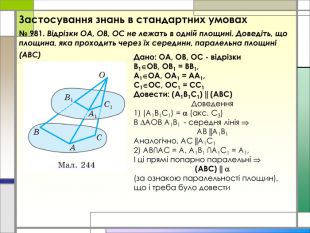
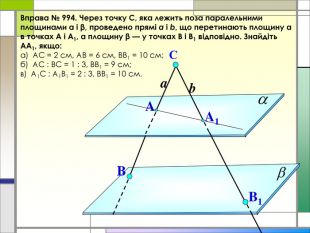
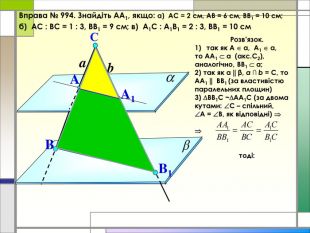

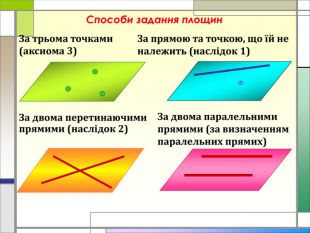
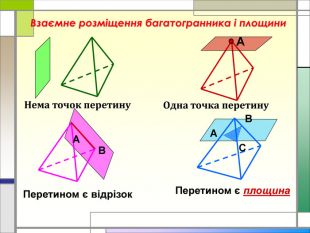

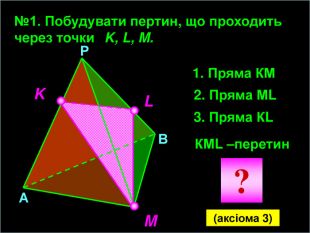
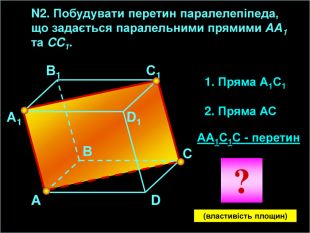
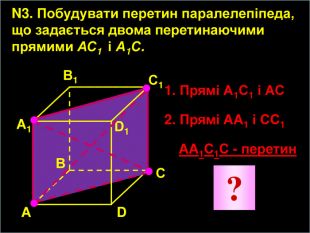
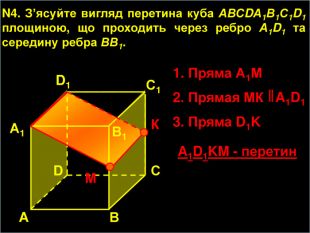
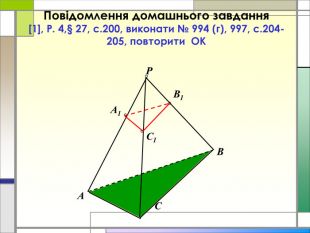
-

Румянцева Оксана Василівна
08.11.2023 в 18:20
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Shaga Tanya
22.11.2022 в 19:15
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Красавіна Вікторія Вячеславівна
06.11.2022 в 20:08
Загальна:
4.7
Структурованість
5.0
Оригінальність викладу
4.0
Відповідність темі
5.0
-

Матвій Галина
01.11.2022 в 09:55
Дякую за чудово продуману і практично наповнену презентацію)))
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Тимченко Олена Василівна
29.11.2021 в 15:21
Відчувається рука майстра. Дякую.
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Сіза Світлана Георгіївна
15.11.2021 в 23:15
Дякую, дуже сподобалась презентація.
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 3 відгука