Презентація. "Паралельне проектування і його властивості. Зображення фігур у стереометрії"
Про матеріал
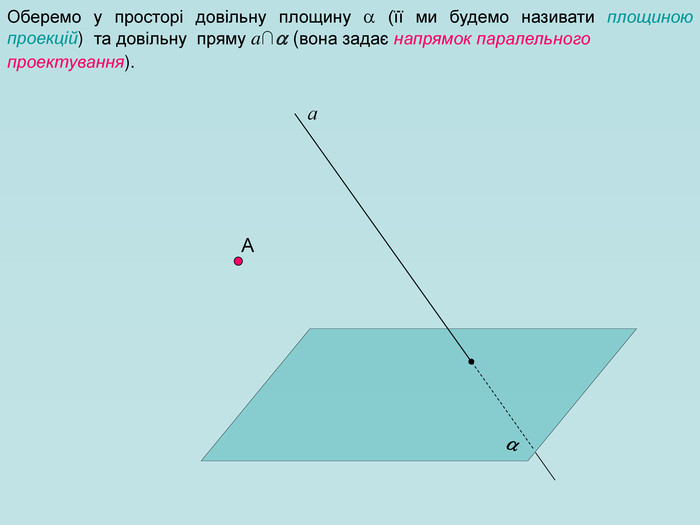
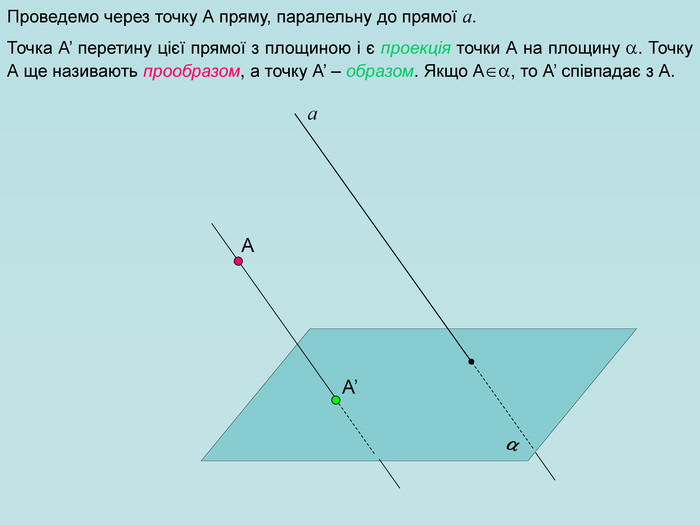
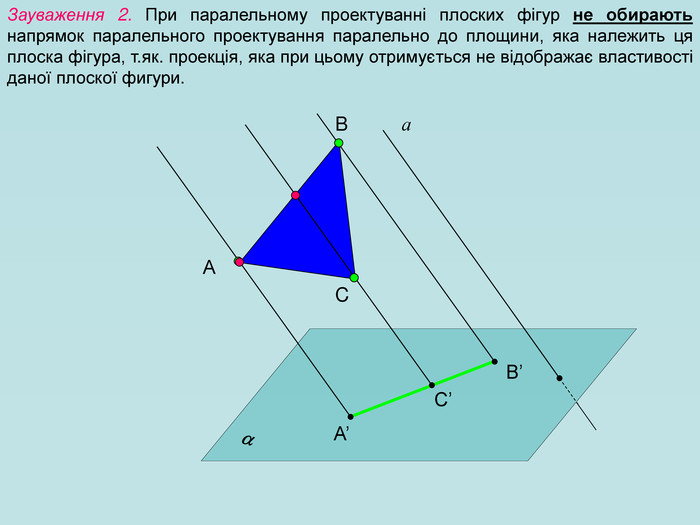
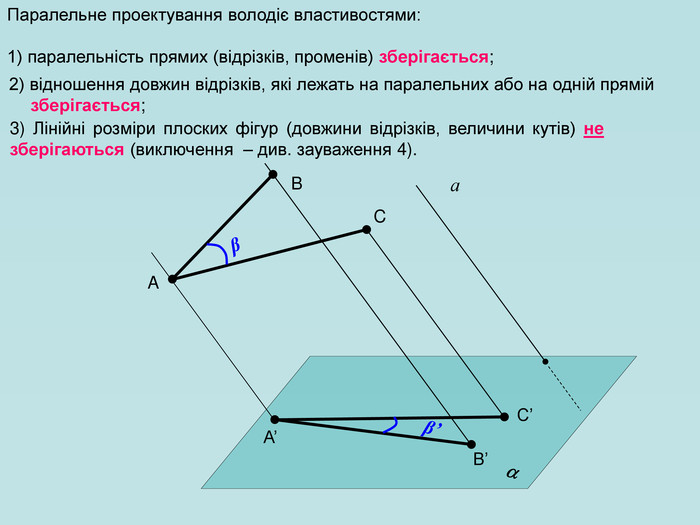
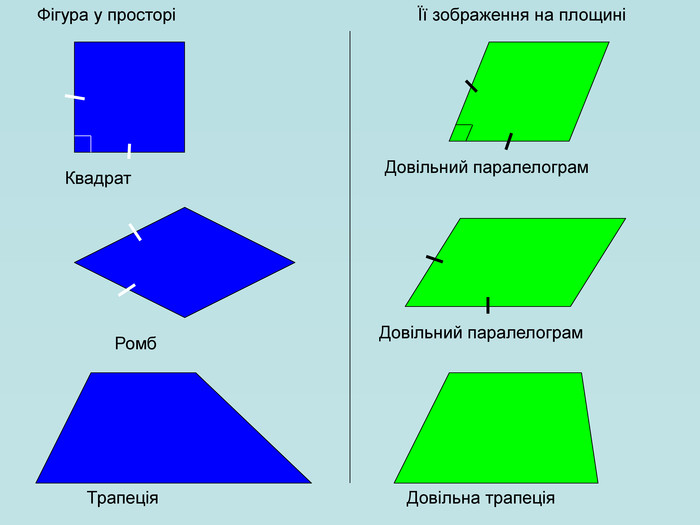
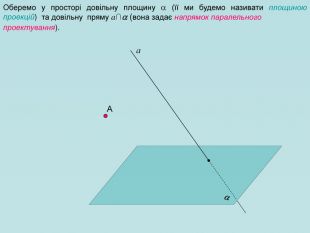
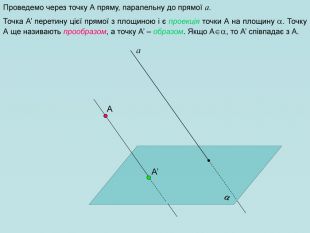
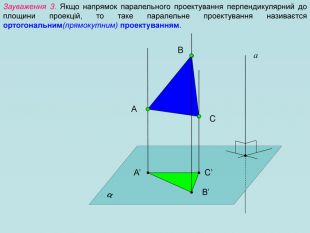
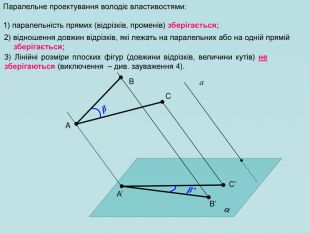
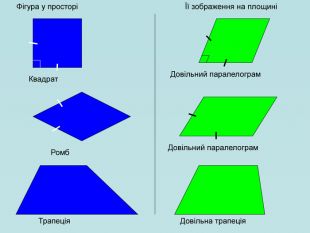
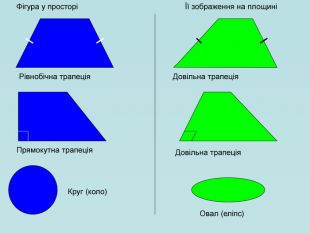
Для зображення просторових фігур у стереометрії користуються паралельним проектуванням. Нехай дано довільну площину α, точку А і пряму h, яке перетинає площину α. Проведемо через точку А пряму, яка паралельна h, вона перетинає площину α у деякій точці А1. Знайдену таким способом точку А; називають паралельною проекцією точки А на площину α у напрямі h. Пряму h називають проектуючою прямою, площину α — площиною проекцій.
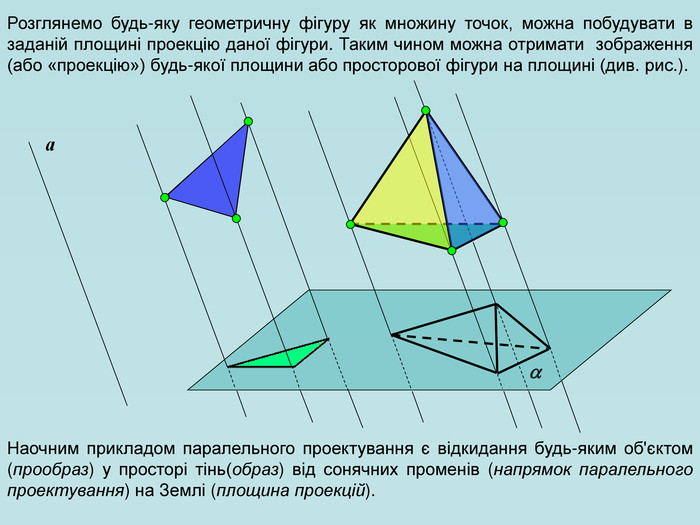
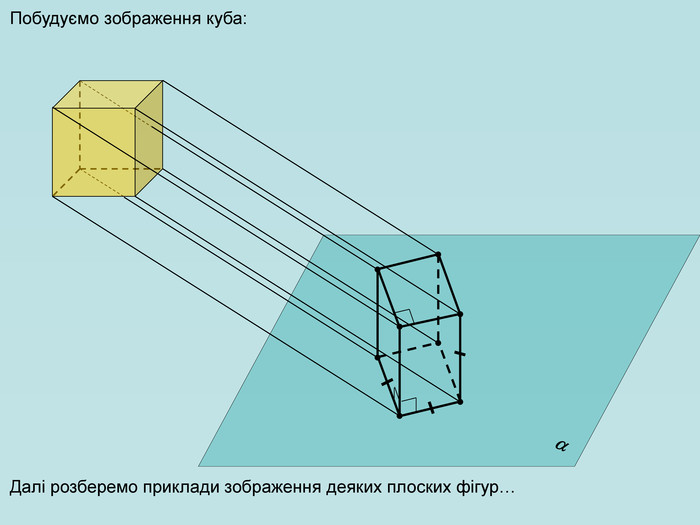
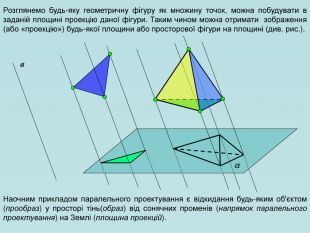
Щоб побудувати проекцію будь-якої фігури, треба спроектувати на площину проекції кожну точку даної фігури. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
ppt
Оцінка розробки

Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку







-

Мисік Марина Олександрівна
27.09.2024 в 11:09
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Мальцева Ірина Миколаївна
07.11.2023 в 18:12
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Приходько Наталія Михайлівна
17.10.2023 в 12:44
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Гозян Тетяна
11.10.2023 в 13:37
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Дубіна Тетяна Станіславівна
03.10.2022 в 14:32
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Сліпченко Олена Юріївна
09.11.2021 в 10:55
Дуже змістовна і цікава презентація. Дякую
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Рогач Тетяна Іванівна
26.10.2021 в 09:50
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Романенко Ірина Леонідівна
03.12.2019 в 13:36
Дякую за презентацію!
Думаю, урок буде вдалим!
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Любоженко Aлла Георгіївна
21.11.2019 в 01:25
Загальна:
4.7
Структурованість
5.0
Оригінальність викладу
4.0
Відповідність темі
5.0
-

Труш Галина
23.10.2019 в 23:33
Загальна:
4.3
Структурованість
4.0
Оригінальність викладу
4.0
Відповідність темі
5.0
Показати ще 7 відгуків