Відкрите заняття з математики "Елементи комбінаторики. Розв'язування комбінаторних задач"

 

План відкритого заняття з математики «Елементи комбінаторики. Розв’язування комбінаторних задач»

 

1. Вид заняття:    Лекційно - практичне

 

2. Дата:                 

 

3. Дисципліна:      Математика

 

4. Група:                  О,Е-21
5. Спеціальності:   073 «Менеджмент»; 076 «Підприємництво, торгівля та біржова        діяльність».  Спеціалізація   «Організація виробництва», «Економіка та підприємництво»
6. Тема заняття:     Елементи комбінаторики. Розв’язування комбінаторних задач.

Мета заняття:	Ознайомити студентів з елементами комбінаторики, а саме з перестановками, розміщеннями, комбінаціями. Пояснити основні правила для розв’язування комбінаторних задач. Узагальнити та систематизувати знання по темі «Елементи теорії ймовірностей».
	Розвивати у студентів  креативне і нестандартне мислення,  допомагати знаходити прості шляхи виходу із ситуації. Розвивати логічне та абстрактне мислення,  математичну культуру мовлення, вміння аналізувати, систематизувати та узагальнювати факти, робити висновки.
	Виховувати у студентів працелюбність, зібраність, організованість, вимогливість до себе. Сприяти вихованню самостійності студентів, наполегливості у пізнанні  нового, уміння чітко формулювати і відстоювати свою думку.

8. Мета відкритого заняття:

             Показати методику проведення лекційно практичного  заняття з  

               елементами особистісно-зорієнтованого навчання.

9. Тип заняття:      

Повідомлення і засвоєння нових знань, формування вмінь та навичок

10.  Методи:              

Інформаційно - розвивальні, проблемно – пошукові, творчо -  продуктивні

11.  Матеріально-технічне забезпечення заняття: 

               комп’ютер, мультимедійний проектор

12.  Навчальне місце (аудиторія чи лабораторія): 

                                               аудиторія №307

 

 

 

Література (основна):

1. М.І.Шкіль «Алгебра і початки ан.10-11 клас», Київ, вид. «Зодіак-еко»,    

1995 р,р.12, §2- §3

2. Є.П.Нелін, О.Є.Долгова «Алгебра і початки ан.11 клас», Харків, вид. «Світ дитинства», 2006р,  розділ 3, §18.

3. А.Г.Мерзляк «Алгебра 11 клас», Харків, вид. «Гімназія», 2011 р,§5 (п.30-п.31).  

 

Література (додаткова):

1. П.Л.Свердан «Вища математика », Київ, вид. «Знання», 2008 р, розділ 8, §8.1-§8.3.

2. М.В.Богомолов «Практичні заняття з математики», Київ вид. «Вища школа», 1983 р, розділ 16,§2.

Структура і хід заняття

 

1. Організаційна частина                                                                                                  до 2 хв

       Привітання, перевірка наявності і підготовки студентів до заняття.

 

2. Актуалізація опорних знань студентів і мотивація навчальної діяльності       до 20 хв                                                                                         

Запитання до студентів

1.  Предмет теорії ймовірностей. Класифікація подій.

2.  Алгебра подій. Властивості операцій додавання і множення подій.

3. Класичне і статистичне означення ймовірності події. Властивості ймовірності.

 

Інтерактивне розв’язування вправ

Мультимедійна презентація на тему «Елементи комбінаторики»

 

3. Повідомлення теми, змісту і послідовності вивчення нового матеріалу             до2 хв

 

Тема заняття: Елементи комбінаторики. Розв’язування комбінаторних задач.  до 30 хв

 

1.  Комбінаторика як наука. Елементи комбінаторики. Види сполук.
2.  Основні правила комбінаторики.
3.  Схема розв’язування комбінаторних задач.
4.   Приклади розв’язування комбінаторних задач.

 

4. Узагальнення і систематизація знань   до 20 хв

       Узагальнення нового матеріалу, шляхом перегляду мультимедійних

   презентацій по темах «З історії теорії ймовірностей», «Цікаві комбінаторні задачі».

 

5. Підсумки роботи студентів     до 4 хв

       Підведення підсумків заняття. Аналіз загальної активності студентів,

шляхом рефлексії.

6. Домашнє завдання     до 2 хв

1. М.І.Шкіль «Алгебра і початки ан.10-11 клас», Київ, вид. «Зодіак-еко», 1995 р,р.12, §2- §3,

стр.445, №17, №18.

2. Є.П.Нелін, О.Є.Долгова «Алгебра і початки ан.11 клас», Харків, вид. «Світ дитинства», 2006р,  розділ 3, §18, стр.238, №5-№7.

 

Пояснення нового матеріалу

        Комбінаторика – розділ математики, в якому вивчаються способи вибору і розміщення елементів деякої скінченної множини на основі певних умов. Вибрані (або вибрані і розміщені) групи елементів називаються сполуками.

         Якщо всі елементи заданої впорядкованої множини різні – дістаємо перестановки без повторень, а якщо в заданій множині елементи повторюються, то дістаємо перестановки з повтореннями.

Означення. Перестановкою з п елементів називається будь-яка впорядкована множина з п елементів.

          Інакше кажучи, це така множина, для якої указано, який елемент знаходиться на першому місці, який – на другому, …, який – на п-му.

Приклад. Скільки різних шестизначних чисел можна скласти з цифр 1, 2, 3, 4, 5, 6 при умові, що цифри в числі не повторюються?

Розв’язання. Кількість чисел буде дорівнювати числу перестановок з шести елементів: 

Приклад. Кур’єр повинен рознести пакети в 7 різних установ. Скільки маршрутів він зможе вибрати.

Розв’язання. Кількість маршрутів буде дорівнювати числу перестановок з семи елементів: 

Означення. Розміщенням з п елементів по називається будь-яка впорядкована множина з елементів, складена з елементів п – елементної множини.

 

Приклад. Скільки різних тризначних чисел можна скласти з цифр 1, 2, 4, 5, 6, 7, якщо цифри в числі не повторюються.

Розв’язання. Кількість тризначних чисел дорівнює числу розміщень з шести елементів по три:

Приклад. Скільки різних трицифрових чисел можна скласти з цифр 1, 2, 3, 4, 5, 6, 0, якщо цифри в числі не повторюються.

Розв’язання. Кількість трицифрових чисел, які можна скласти з семи цифр, дорівнює числу розміщень із семи елементів по три, тобто .

Але серед даних цифр є цифра 0, з якої не може починатися трицифрове число. Кількість таких чисел буде дорівнювати числу розміщень із шести елементів по два:

 

Означення. Комбінацією з п елементів по називається будь-яка -елементна підмножина, складена з п – елементної множини.

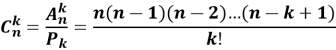
Деякі властивості числа комбінацій без повторень:

Приклад. Із класу, що складається з 25 учнів треба вибрати 3 на чергування. Скількома способами це можна зробити?

Розв’язання. Кількість способів дорівнює числу комбінацій з 25 елементів по 3.

Приклад. Під час зустрічі 16 осіб потисли один одному руки. Скільки всього зроблено рукостискань?

Розв’язання. Кількість рукостискань дорівнює числу комбінацій з 16 елементів по 2.

Розглянемо схему розв’язування комбінаторних задач. Спочатку вибираємо правило.

Правило суми. Якщо елемент А можна вибрати m способами, а елемент В

n способами, то елемент А або В можна вибрати (m + n) способами.

Правило добутку. Якщо елемент А можна вибрати m способами, а після елемент В - n способами, то елемент А і В можна вибрати (m n) способами.

Вибір формули

Чи враховується порядок слідування елементів у сполуці?

 Так     Ні

Чи усі елементи входять у сполуку?                                      Комбінації

Так Ні

Перестановки                        Розміщення

 

Комбінаторні задачі для закріплення даної теми

1. Скількома способами можна розділити 20 підручників з фізики між 18 учнями?

Розв’язання. Кількість способів буде дорівнювати числу комбінацій з 20         елементів по 18.

2. Із вази, у якій 10 різних  яблук і 5 різних груш, потрібно вибрати 3 яблука і 2 груші. Скількома способами це можна зробити?

Розв’язання. Кількість способів буде дорівнювати добутку числа комбінацій з 10 елементів по 3 і 5 елементів по 2.

3. Студент пам’ятає, що телефон його товариша закінчується цифрами 2, 3, 4, 5, але забув, у якому порядку вони розміщені. Укажіть, яке найбільше число варіантів, яке йому доведеться перебрати, щоб додзвонитися товаришу?

Розв’язання. Кількість способів буде дорівнювати числу розміщень з 10         елементів по 4.

4. Скільки серед чотирицифрових чисел, складених із цифр 3, 5, 7, 9 без повторення, є таких, які: а) починаються з цифри 3; б) кратні 5?

Розв’язання. а) кількість чисел, які починаються з цифри 3, буде дорівнювати числу перестановок з 3 елементів.

б) кількість чисел кратних 5 буде дорівнювати числу перестановок з 3        

елементів.

5. Скількома різними способами збори, що складаються з 40 осіб, можуть обрати зі свого числа голову зборів, його заступника і секретаря?

Розв’язання. Кількість способів буде дорівнювати числу розміщень з 40         елементів по 3.

6. Розв’язати комбінаторне рівняння: