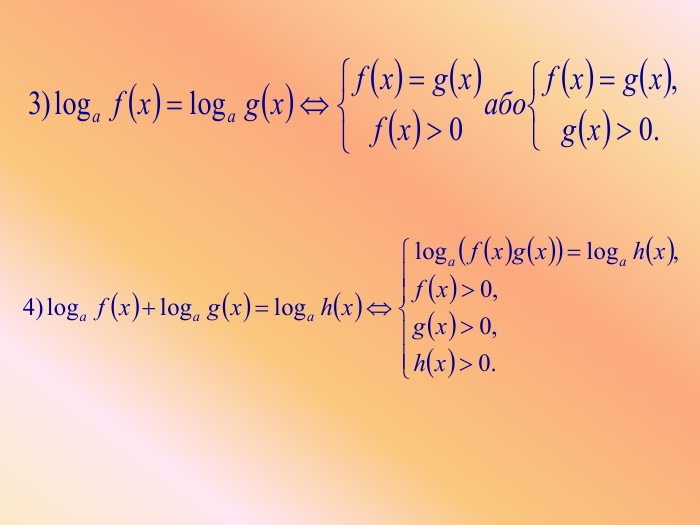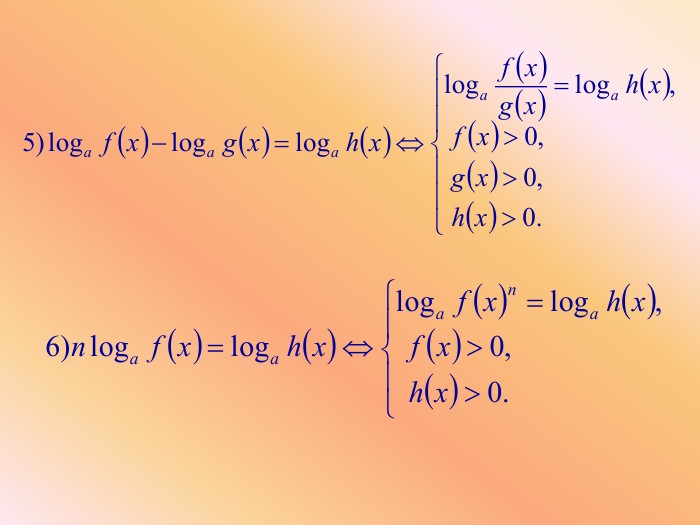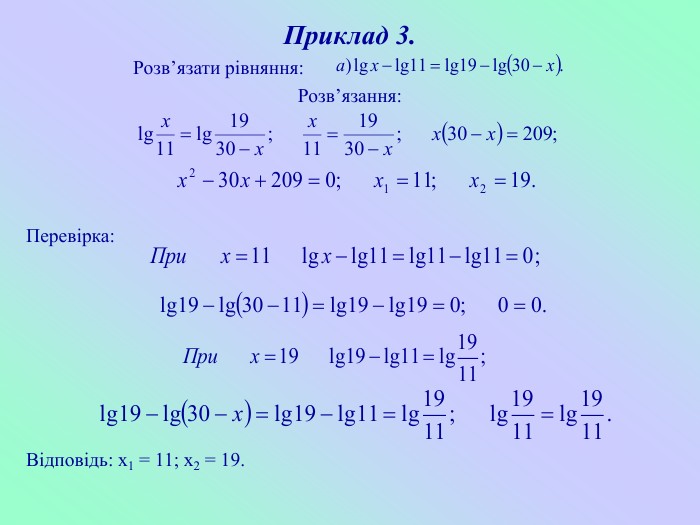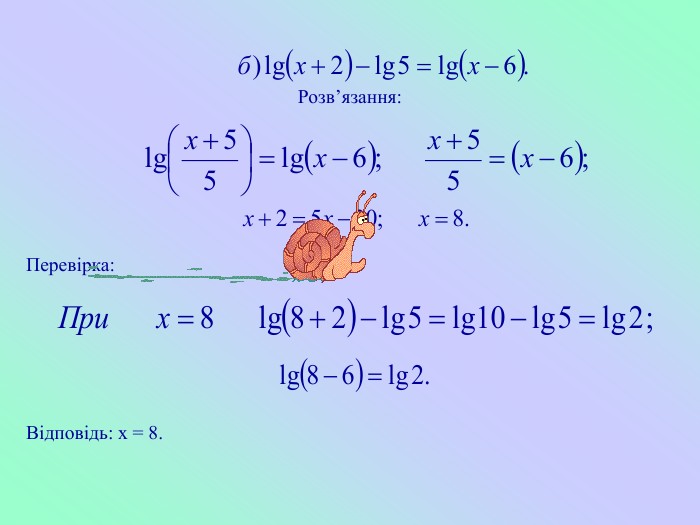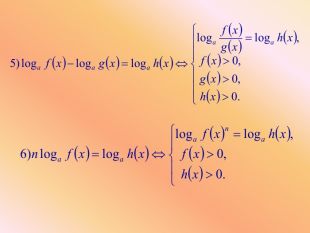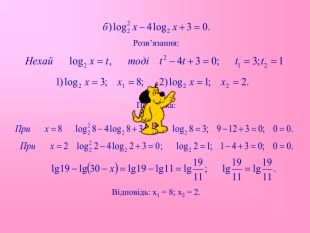Відкритий урок і презентація з алгебри і початків аналізу. Розв'язування логарифмічних рівнянь.

Відкритий урок з алгебри і початків аналізу.

11 клас

Тема уроку:

Розв'язування  логарифмічних рівнянь.

Мета уроку:

• Вчити учнів  розв'язувати логарифмічні рівняння різними способами. Відпрацювати уміння розв’язувати найпростіші логарифмічні  рівняння.  
• Розвивати в учнів  старанність, культуру відповіді, логічну увагу, критичність і швидкість розв'язування.
• Вчити висловлювати свою думку, бути відповідальним за спільну справу, оцінювати свою роботу і роботу своїх товаришів.     

Принципи навчання на уроці:

• Взаємодопомога;
• Взаємоповага;
• Постійне самовдосконалення;
• Захист своїх інтересів;
• Обґрунтування своїх думок та думок товариша.

Об’єкт контролю на уроці:

• Правильність виконання завдань;
• Охайність і дотримання єдиних вимог до оформлення завдань;
• Швидкість роботи;
• Взаємоповага під час спілкування;
• Коректність стосунків учнів.

Тип уроку:

                      Вивчення нового матеріалу.

Структура уроку:

1. Організаційний момент.
2. Перевірка домашнього завдання.
3. Повторення вивченого матеріалу на попередніх уроках.
4. Тематичне тестування.
5. Вивчення нового матеріалу.
6. Підсумок уроку.
7. Домашнє завдання.

 

Хід уроку:

1. Організаційний момент.

   Повідомлення теми і мети уроку.

2. Перевірка домашнього завдання.

   Наявність письмового завдання перевіряють консультанти.

3. Повторення вивченого матеріалу на попередніх уроках.

Учні дають усну відповідь на поставлені вчителем питання.  

1. Що називається логарифмом числа за даною основою?
2. Назвати основну логарифмічну тотожність.
3. Який логарифм називається десятковим?
4. Властивості логарифмів.
5. Що називається логарифмуванням?
6. Що називається потенціюванням?
7. Накреслить схематично графік логарифмічної функції.
8. Властивості логарифмічної функції.

4. Тематичне оцінювання.

   Учні одержують картки з Тестові завдання по темі «Логарифмічна функція».

      Після розв’язання вони обмінюються роботами і звіряють відповіді, які     

      проектуються на дошці. 

      Кожне вірно розв’язане завдання оцінюється в 0,5 бала.

 

 

 

Тестові завдання по темі

«Логарифмічна функція»

І в

1. Обчисліть значення виразу:

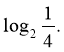
А) 2;     Б) -2;    В) 4;    Г) -4.

2. Не виконуючи побудови знайдіть точку перетину графіка функції:

з віссю абсцис.

А) (-2;0);   Б) (3;0);   В) (2;0);   Г) (1;0).

3. Знайдіть область визначення функції:

               

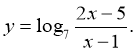
4. Застосовуючи властивості логарифмічної функції, визначити, що більше:

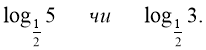
        Г) не визначено.

Відповідь:

 

А      Б     В     Г

                                    1

                                    2

                                    3

                                   4
 

 

 

Тестові завдання по темі

«Логарифмічна функція»

ІІ в

1. Обчисліть значення виразу:

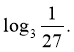
А) 27;     Б) 3;    В) -3;    Г) 27^-1.

2. Не виконуючи побудови знайдіть точку перетину графіка функції:

з віссю абсцис.

А) (4;0);   Б) (1;0);   В) (-3;0);   Г) (-4;0).

3. Знайдіть область визначення функції:

                 

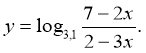
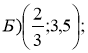
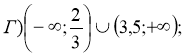
4. Застосовуючи властивості логарифмічної функції, визначити, що більше:

        Г) не визначено.

Відповідь:

 

А      Б     В     Г

                                    1

                                    2

                                    3

                                   4
 

 

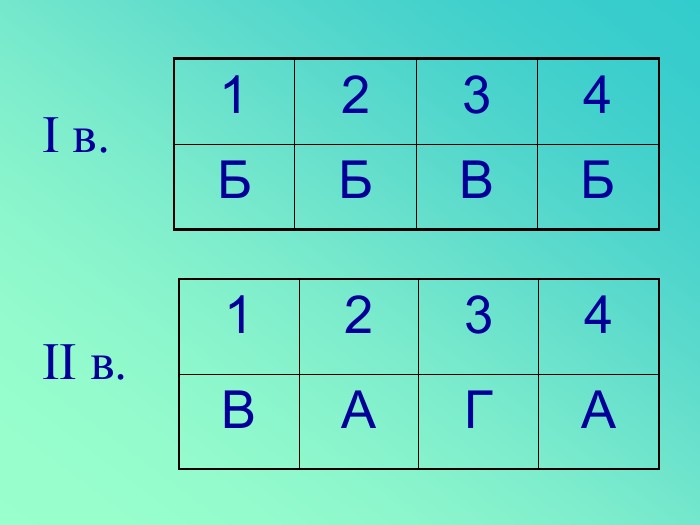
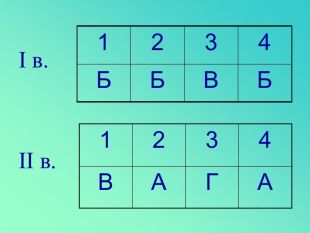
Відповідь:

1	2	3	4
Б	Б	В	Б

 

І в.

 

1	2	3	4
В	А	Г	А

 

ІІ в.

 

 

  V.   Вивчення нового матеріалу.

Пояснення вчителя:

Логарифмічними називаються рівняння, які містять зміну під знаком логарифма.

Наприклад:

         log ₂ (3x - 2) = 4, lg x + lg 5 = 2,  lg (3 x² + 7) – lg (3 x – 2) = 1.  Рівняння

не є логарифмічним, бо воно не містить невідомого під знаком логарифма.

 Розв'язування логарифмічних рівнянь ґрунтується на означені логарифма, властивостях логарифмічної функції та властивостях логарифма.

Основні методи розв'язування логарифмічних рівнянь

         

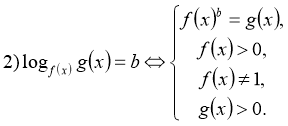
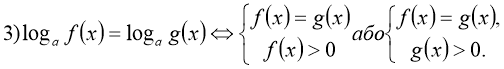
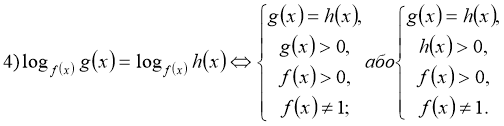
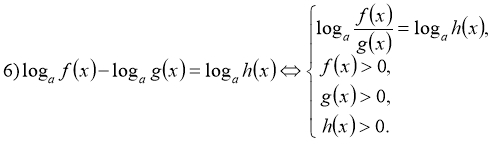
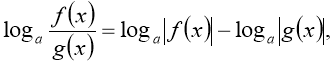
 Учні консультанти розв’язують і пояснюють підготовлені ними приклади і пропонують учням класу розв’язати самостійно аналогічний приклад б, слідкують за розв’язуванням і оцінюють роботу кожного учня в 1 бал.

 

Приклад 1.

Розв’язати рівняння: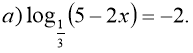        

Розв’язання:

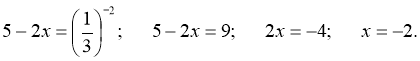
Перевірка:

Відповідь: х = -2.

Розв’язання:

Перевірка:

Відповідь: х = 5.

 

Приклад 2.

Розв’язати рівняння:      

Розв’язання:

Перевірка:

Вираз не має змісту.

Відповідь: Рівняння коренів не має.

Розв’язання:

Перевірка:

Відповідь: х = 8.

 

 

Приклад 3.

Розв’язати рівняння:   

Розв’язання:

Перевірка:

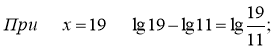
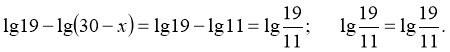
Відповідь: х₁ = 11; х₂ = 19.

Розв’язання:

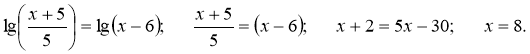
Перевірка:

Відповідь: х = 8.

 

Приклад 4.

Розв’язати рівняння:        

Розв’язання:

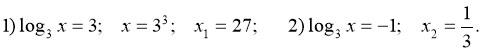
Перевірка:

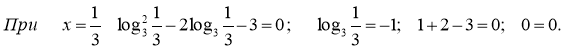
Відповідь:

Розв’язання:

Перевірка:

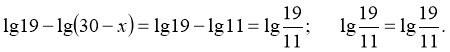
Відповідь: х₁ = 8; х₂ = 2.

 

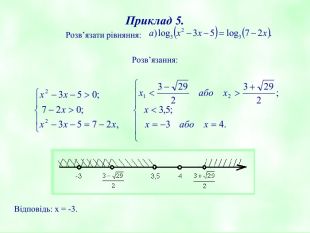
Приклад 5.

Розв’язати рівняння:       

Розв’язання:

 

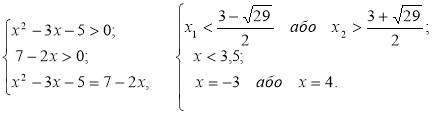
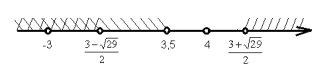
Відповідь: х = -3.

Розв’язання:

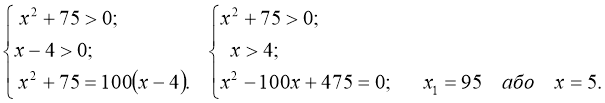
Відповідь: х₁ = 95; х₂ = 5.

6. Підсумок уроку.

          Учитель аналізує роботу кожного учня.

7. Домашнє  завдання.

1. § 23 № 228 (5, 9); 229 (5, 7).
2. Додаткове завдання № 230 (4).
3. Повторити формули § 21, 20 № 175 (19).

 

Дякую за урок!