Відкритий урок "Теорема Піфагора"

УРОК

Тема уроку. Розв'язування прямокутних трикутників.

Мета уроку: узагальнити і систематизувати знання з даної теми; повторити теорему Піфагора та основні наслідки з неї; закріпити вміння і навички застосувати теоретичний матеріал до розв'язування прямокутних трикутників; показати практично-прикладний характер здобутих знань; розвивати логічність і послідовність дій при розв’язувані задач; виховання пізнавального інтересу до вивчення математики.

Розвиваюча: розвивати вміння учнів використовувати набуті навички під час розв'язування задач;

Виховна: виховувати наполегливість, вміння об’єктивно оцінювати здібності;

Компетенції (соціальна та громадянська компетентності):

•    Уміння: висловлювати власну думку, слухати і чути інших, оцінювати аргументи та змінювати думку на основі доказів; аргументувати та відстоювати свою позицію; співпрацювати в команді, виділяти та виконувати власну роль в командній роботі;
•    Ставлення: ощадливість і поміркованість; рівне ставлення до інших незалежно від статків, соціального походження; відповідальність за спільну справу; налаштованість на логічне обґрунтування позиції без передчасного переходу до висновків; повага до прав людини, активна позиція щодо боротьби із дискримінацією.

Тип уроку: застосування умінь і навичок.

Обладнання: підручник, роздавальні матеріали, проектор, ноутбук

Хід уроку

І. Організаційний момент

Привітання
Перевірка присутніх на уроці
Налаштування на роботу

ІІ. Перевірка домашнього завдання

Теорема Піфагора — це основа евклідової геометрії, завдяки їй доводиться більшість теорем геометрії, тому її необхідно добре засвоїти. Домашнім завданням була задана пошукова робота, знайти різні способи доведення теореми Піфагора.

Перевірити, як справилися учні із завданням. Один із способів продемонструвати біля дошки.

ІII. Актуалізація опорних знань учнів

Проводиться у формі тесту застосовуючи програму PLICKERS.

ІV. Формулювання теми, мети і задач уроку

Теорема Піфагора по праву вважається найважливішою в курсі геометрії й заслуговує на пильну увагу.  Вона є основою розв'язування багатьох геометричних задач і базою вивчення теоретичного курсу надалі; містить багатий історичний матеріал.

V. Закріплення навичок і вмінь учнів розв'язувати прямокутні трикутники

Розв’язування задач біля дошки:

1.               Основа рівнобедреного трикутника 16см, а висота, проведена до основи, дорівнює 6 см. Знайдіть бічну сторону трикутника.
2.               Діагональ прямокутника дорівнює 10см, а одна з його сторін 8 см. Знайдіть периметр прямокутника.

Задача із збірника ЗНО-2014, №24

Фізкультхвилинка

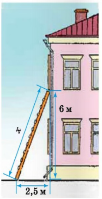
Для самостійного виконання:

1) Якої довжини має бути драбина, щоб її можна було приставити до вікна, розташованого на висоті 6 м, якщо відстань від нижнього кінця драбини до будинку має дорівнювати 2,5 м?

2) На яку відстань від стіни будинку потрібно відсунути нижній кінець драбини завдовжки 9 м, щоб верхній її кінець, був на висоті 6 м?

VІ. Підбиття підсумків уроку

Вправа «Знайти зашифроване слово» (УСПІХ)

1. Використайте теорему Піфагора для трикутника KLM, у якого = 90°.

А) КМ² = КL² + МL²;  У) КL² = КМ² + МL²;  В) МL² =КL² + КМ².

2.  Використайте наслідок з теореми Піфагора для трикутника АВС, у якого = 90°. 

О) АВ = ;   К) ВС = ;  С) АВ =

3. Якщо в трикутнику PRS виконується рівність PS² = PR² + RS², то прямим кутом є:

А) П) ;  Л)

4. Знайдіть гіпотенузу прямокутного трикутника, якщо катети дорівнюють см і 1 см.

Б) 3;  В) 1;  І) 2.

5. Знайдіть катет прямокутного трикутника, якщо гіпотенуза і другий катет відповідно дорівнюють см і 1 см.

Л) 1;  Х) 2;  М) 3. 

VIІ. Вихідна рефлексія.

1. Що сьогодні на уроці було найважливішим ?

2. Що на уроці було цікавим ?

3. Що викликало ускладнення, труднощі?

4. Над чим слід попрацювати вдома.

VIІІ. Домашнє завдання

1) Пар. 3, п.18, ст. 129-133

2) № 616

3) Скласти задачу практичного змісту, яку можна розв'язати за допомогою теореми Піфагора.